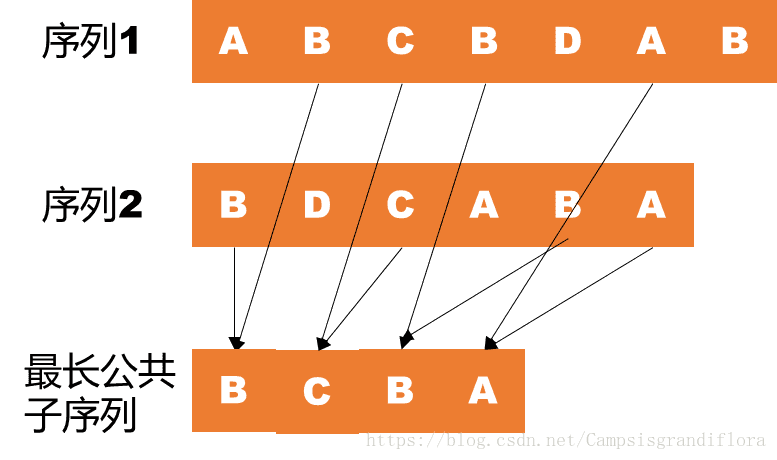算法课堂实验报告（四）——python动态规划（最长公共子序列LCS问题）

python实现动态规划

---

一、开发环境

开发工具：jupyter notebook 并使用vscode，cmd命令行工具协助编程测试算法,并使用codeblocks辅助编写C++程序
编程语言：python3.6

二、实验内容

1.最长公共子序列问题。分别求x={ABCBDAB}, y={BDCABA}

问题背景：

首先引用一下百度百科的话

最长公共子序列（LCS）是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题。一个数列 ，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则称为已知序列的最长公共子序列。

LCS问题具有广泛的应用，和生物信息学应用的基础，它也被广泛地应用在版本控制，比如Git用来调和文件之间的改变

子序列和子串的区别就是，子串要求字符串连续而子序列没有这种要求。

以一张简单的图说明一下什么是最长公共子序列

求解LCS问题有很多很多种方法，其中动态规划算法算是其中一种，将两个序列分别记为X和Y，X序列元素分别为{x1，x2……，xn}，Y序列元素分别为{y1，y2,……ym}，如果xn＝ym，这个问题就可以转化为求xn-1和ym-1两个序列的最大公共子序列问题，如果不相等，则要求两个子问题，即Xn-1与Y还有X与Ym-1两个最长公共子序列问题。

下面我们来一步一步解决这个问题，我们可以从这个问题的子问题开始考虑，建立一张表a，用于记录子问题的最长公共子序列元素的个数，表格中ix和jy表示序列1取前x个数和序列2取前y个数的最长公共子序列元素个数，i0和j0当然全部填0。

	j0	j1	j2	j3	j4	j5	j6
i0	0	0	0	0	0	0	0
i1	0
i2	0
i3	0
i4	0
i5	0
i6	0
i7	0

首先考虑序列x={A},y={B}的情况，此时序列1只有A这个元素，序列2只有B这个元素，肯定不匹配，所以这个字问题的最长公共子序列元素个数为0，所以我们在(i1，j1)这个格子上填上0。（图示中红色的两位代表不匹配，橙色代表序列中的元素，绿色代表匹配成功）

接下来我们考虑序列x={A}, y={BD}的情况，同样为最后一位不匹配，所以我们在(i1，j2)填上0。

然后是x={A},y={BDC}的情况，因为最后一位不匹配，所以在(i1.j3)上填上0。

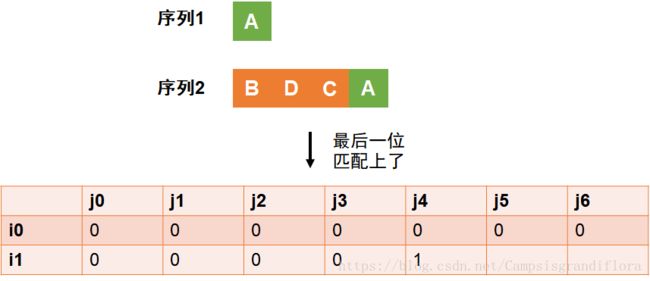
但是，当我们考虑问题x={A},y={BDCA}的时候，发现最后一位匹配上了，我们可以这样考虑，x={A}，y={BDCA}这个问题是在问题x={}，y={BDC}这个问题的基础上再加最后的A，所以(i1，j4)上填的是(i0，j3)+1，所以这个格子上填上1

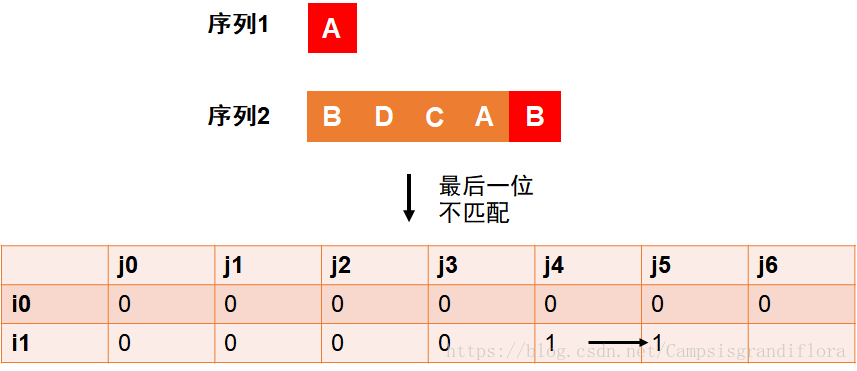
问题继续，当考虑问题x={A},y={BDCAB}时，发现最后一位不匹配，当时(i1，j5)这个问题可以看做是(i1，j4)或(i0，j5)这个问题填上了一位，所以在这个格子上，我们取(i1，j4)和（i0，j5）中的最大值填上。

按照这样的规则，我们可以依次填完整张表格，最终的答案就是（i7，j6）为4

	j0	j1	j2	j3	j4	j5	j6
i0	0	0	0	0	0	0	0
i1	0	0	0	0	1	1	1
i2	0	1	1	1	1	2	2
i3	0	1	1	2	2	2	2
i4	0	1	1	2	2	3	3
i5	0	1	2	2	2	3	3
i6	0	1	2	2	3	3	4
i7	0	1	2	2	3	4	4

在这个过程中，我们建立表b，为了确定a表中某个值是从哪里来的，如果(ix,jy)的值是因为(ix-1，jy-1)+1而填上的，我们就在b(i，j)这个位置上填1，如果(ix，jy)是从（ix-1，iy）继承过来的，在b（i，j）上填上2，如果是从（ix，jy-1）继承过来的，就在b（i，j）填上3，利用b表可以根据回溯法确定最长公共子序列具体的元素。

这个算法利用了动态规划的思想，时间复杂度为O（n²）,代码如下：

# 最长公共子序列问题
import numpy as np

def LCSLength(m, n, x, y, a, b):
    for i in range(1,m+1):
        for j in range(1,n+1):
            if x[i-1]==y[j-1]:
                a[i][j] = a[i-1][j-1]+1
                b[i][j] = 1
            elif a[i-1][j] >= a[i][j-1]:
                a[i][j] = a[i-1][j]
                b[i][j] = 2
            else:
                a[i][j] = a[i][j-1]
                b[i][j] = 3

def LCS(i, j, x, b):
    if i==0 or j==0:
        return
    if b[i][j]==1:
        LCS(i-1, j-1, x, b)
        print(x[i-1])
    elif b[i][j]==2:
        LCS(i-1, j, x, b)
    else:
        LCS(i, j-1, x, b)
        
x= "ABCBDAB"
y= "BDCABA"

lenx = len(x)
leny = len(y)

a = np.zeros((lenx+1)*(leny+1)).reshape((lenx+1), (leny+1))    # 生成一个m*n且全是0的矩阵
b = np.zeros((lenx+1)*(leny+1)).reshape((lenx+1), (leny+1))    # 再来一个m*n且全是0的矩阵

LCSLength(lenx, leny, x, y, a, b)