数据结构之（一）Hash（散列）

最近一直在准备面试，借此机会把数据结构相关整理一下，方便自己和其他人查阅。
该系列第一篇为Hash，主要考察点相对集中，对研发和测试的面试来说深度要求也不算太高，因此主要整理Hash数据结构的相关知识点，追求广度和部分深度。下面以基础概念（Hash（散列，下文统一称hash、hash表）、hash表（散列表）、常用哈希构造方法及函数、避免哈希冲突常用方法）、几种常用的查找数据结构的对比、STL常见的hash实现。

基础概念

---

哈希：哈希是一种用以常数平均时间执行插入、删除和查找的技术。但是，一般不支持诸如FindMin、FindMax以及以线性时间按排序顺序将整个表进行打印的操作。进一步讲，hash就是把任意长度的输入（预映射， pre-image），通过散列算法，变换成固定长度的输出，该输出就是散列值。

哈希表：利用hash技术实现，理想情况下为一个包含有关键字（key-indexed，可以为整数、字符串等）的具有固定大小的数组。输入待查找的值即关键字，即可查找到其对应的数据元素。

哈希函数：建立起数据元素的存放位置与数据元素的关键字之间的对应关系的函数。即使用哈希函数可将被查找的键转换为数组的索引。理想情况下它应该运算简单并且保证任何两个不同的关键字映射到不同的单元（索引值）。但是，这是不可能的，很多时候我们都需要处理多个键被哈希到同一个索引值的情况，即哈希碰撞冲突。

那么为什么很难达到理想情况呢？
我们考虑如果没有内存限制，那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1)。但实际上我们很难忽略内存的影响，在例如处理海量数据时，hash往往是一种很好的方式，但这时内存一般不能满足数据要求，所以就需要考虑解决冲突。

哈希函数

---

如上所述，我们通常希望尽量寻找一个hash函数，该函数尽量在单元之间均匀地分配关键字，并且计算简单。综合不同因素，常用的哈希函数构造方法有以下几种：

1、直接寻址法：以关键字的某个线性函数值为哈希地址，可以表示为hash(K)=aK+C
优点是不会产生冲突，缺点是空间复杂度可能会较高，可能会造成空间的大量浪费，适用于元素较少的情况

2、数字分析法：该方法是取数据元素关键字中某些取值较均匀的数字来作为哈希地址的方法，这样可以尽量避免冲突。
缺点是该方法只适合于能预先估计出全体关键字的每一位上各种数字出现的频度。对于想要设计出更加通用的哈希表并不适用。

例如，要构造一个数据元素个数n=80,哈希长度m=100的哈希表。不失一般性，我们这里只给出其中8个关键字进行分析，8个关键字如下所示：

K1=61317602 K2=61326875 K3=62739628 K4=61343634

K5=62706815 K6=62774638 K7=61381262 K8=61394220

分析上述8个关键字可知，关键字从左到右的第1、2、3、6位取值比较集中，不宜作为哈希地址，剩余的第4、5、7、8位取值较均匀，可选取其中的两位作为哈希地址。设选取最后两位作为哈希地址，则这8个关键字的哈希地址分别为：2，75，28，34，15，38，62，20。

3、除留余数法：是由数据元素关键字除以某个常数所留的余数为哈希地址，该方法计算简单，适用范围广，是经常使用的一种哈希函数，可以表示为：hash(K)=K mod C
该方法的关键是常数的选取，一般要求是接近或等于哈希表本身的长度，研究理论表明，该常数选素数时效果最好

4、平方取中法：对关键字计算平方，然后根据可使用空间的大小取中间分布较均匀的几位，散列到相应的位置。
这样计算的原因是因为关键字的大多数位或所有位对结果都有贡献，并且通过取平方扩大差别，平方值的中间几位(位数可用lgN计算）和这个数的每一位都相关，则对不同的关键字得到的哈希函数值不易产生冲突，由此产生的哈希地址也较为均匀。

例如，设哈希表长为1000则可取关键字平方值的中间三位，如下：

关键字	关键字的平方	哈希函数值
1234	1522756	227
2143	4592449	924
4132	17073424	734
3214	10329796	297

有人曾用“轮盘赌”的统计分析方法对它们进行了模拟分析，结论是平方取中法最接近“随机化”。

此法也可应用于字符串的散列
例如，设有一组关键字值为ABC，BCD，CDE，DEF其相应的机内码分别为010203，020304，030405，040506。假设可利用地址空间大小为1000，平方后取平方数的中间三位作为相当记录的存储地址。如下所示：

关键字	机内码	机内码的平方	哈希地址
ABC	010203	0104101209	101
BCD	020304	0412252416	252
CDE	030405	0924464025	464
DEF	040506	1640736036	736

5、折叠法：所谓折叠法是将关键字分割成位数相同的几部分（最后一部分的位数可以不同），然后取这几部分的叠加和（舍去进位），这方法称为折叠法。两种叠加处理的方法：移位叠加:将分割后的几部分低位对齐相加；边界叠加:从一端沿分割界来回折叠，然后对齐相加。

例如，当哈希表长为1000时，关键字key=110108331119891，允许的地址空间为三位十进制数，则这两种叠加情况如图（2）：

   移位叠加                                 边界叠加

   8 9 1                                     8 9 1

   1 1 9                                     9 1 1

   3 3 1                                     3 3 1

   1 0 8                                     8 0 1

+  1 1 0                                   + 1 1 0              

   (1) 5 5 9                     (2)0 4 4

这种方法适用于关键字位数较多，而且关键字中每一位上数字分布大致均匀的情况。同时，此法也可应用于字符串的散列，计算的方法是将字符串的 ASCII 值累加起来，对 M 求模。

6、随机数法：设定哈希函数为:H(key) = Rand(key)，其中，Rand 为伪随机函数
此法适合于对长度不等的关键字构造哈希函数。

7.旋转法：旋转法是将数据的键值中进行旋转。旋转法通常并不直接使用在哈希函数上，而是搭配其他哈希函数使用。

例如，某学校同一个系的新生（小于100人）的学号前5位数是相同的，只有最后2位数不同，我们将最后一位数，旋转放置到第一位，其余的往右移。

新生学号	旋转过程	旋转后的新键值
5062101	506210 1	1506210
5062102	506210 2	2506210
5062103	506210 3	3506210
5062104	506210 4	4506210
5062105	506210 5	5506210

运用这种方法可以只输入一个数值从而快速地查到有关学生的信息。

实际造表时，采用何种构造哈希函数的方法取决于建表的关键字集合的情况(包括关键字的范围和形态)，以及哈希表长度（哈希地址范围），总的原则是使产生冲突的可能性降到尽可能地小。

8、相乘取整法：首先用关键字key乘上某个常数A(0< A<1)，并抽取出key.A的小数部分；然后用m乘以该小数后取整

函数冲突处理方法

---

1、开放地址法（再散列法）：当关键字key的哈希地址p=H（key）出现冲突时，以p为基础，产生另一个哈希地址p1，如果p1仍然冲突，再以p为基础，产生另一个哈希地址p2，…，直到找出一个不冲突的哈希地址pi ，将相应元素存入其中。这种方法有一个通用的再散列函数形式：

Hi=（H（key）+di）%m，i=1，2，…，n

其中H（key）为哈希函数，m 为表长，di称为增量序列。增量序列的取值方式不同，相应的再散列方式也不同。主要有以下几种：

（1）线性探测法：

di=1，2，3，…，m−1

这种方法的特点是：冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表。
建立在两个假设基础上：（1）表格足够大（2）每个元素都能够独立

（2）二次探测法：

di=12，−12，22，−22，…，k2，−k2(k<=m/2）

这种方法的特点是：冲突发生时，在表的左右进行跳跃式探测，比较灵活。

（3）伪随机探测法：

di=伪随机数序列

具体实现时，应建立一个伪随机数发生器，（如 i=(i+p)%m ），并给定一个随机数做起点。

例如：
已知哈希表长度m=11，哈希函数为：H（key）= key % 11，则对于序列47,26,60,69 有
H（47）=3，H（26）=4，H（60）=5，H（69）=3 ，69与47冲突。

（1）用线性探测再散列处理冲突：
下一个哈希地址为 H1=（3+1）%11=4 ，
仍然冲突，再找下一个哈希地址为 H2=（3+2）%11=5 ，
还是冲突，继续找下一个哈希地址为 H3=（3+3）%11=6 ，
此时不再冲突，将69填入5号单元。
平均查找长度为 (1+1+1+4)/4=7/4
（2）用二次探测再散列处理冲突：
下一个哈希地址为 H1=（3+12）%11=4 ，
仍然冲突，再找下一个哈希地址为 H2=（3−12）%11=2 ，
此时不再冲突，将69填入2号单元
平均查找长度为 (1+1+1+3)/4=6/4
（3）:用伪随机探测再散列处理冲突：且伪随机数序列为：2，5，9，……..，
则下一个哈希地址为 H1=（3+2）%11=5 ，
仍然冲突，再找下一个哈希地址为 H2=（3+5）%11=8 ，
此时不再冲突，将69填入8号单元。
平均查找长度为 (1+1+1+3)/4=6/4

从上述例子可以看出，线性探测再散列容易产生“二次聚集”，即在处理同义词的冲突时又导致非同义词的冲突。例如，当表中i, i+1 ,i+2三个单元已满时，下一个哈希地址为i, 或i+1 ,或i+2，或i+3的元素，都将填入i+3这同一个单元，而这四个元素并非同义词。

不过线性探测再散列的优点也很明显：只要哈希表不满，就一定能找到一个不冲突的哈希地址，而二次探测再散列和伪随机探测再散列则不一定。

2、链地址法（拉链法）：
这种方法的基本思想是将所有哈希地址为i的元素构成一个称为同义词链的单链表，并将单链表的头指针存在哈希表的第i个单元中，因而查找、插入和删除主要在同义词链中进行。

例如，已知一组关键字（32，40，36，53，16，46，71，27，42，24，49，64），哈希表长度为13，哈希函数为： H（key）=key%13 ，

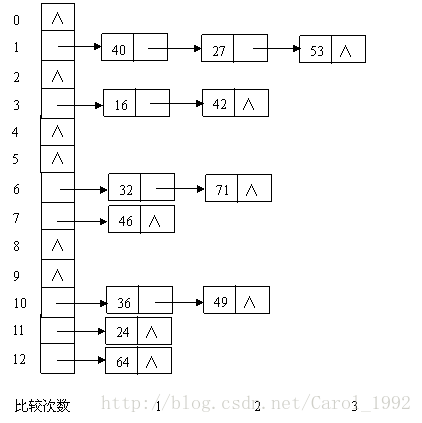
由于链表的特点是：寻址困难，插入和删除容易，链地址法适用于经常进行插入和删除的情况。

与开放定址法相比，拉链法有如下几个优点：
(1) 拉链法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短；
(2) 由于拉链法中各链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况；
(3) 开放定址法为减少冲突，要求装填因子α较小，故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1，且结点较大时，拉链法中增加的指针域可忽略不计，因此节省空间；
(4) 在用拉链法构造的散列表中，删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。而对开放地址法构造的散列表，删除结点不能简单地将被删结点的空间置为空，否则将截断在它之后填人散列表的同义词结点的查找路径。这是因为各种开放地址法中，空地址单元(即开放地址)都是查找失败的条件。因此在用开放地址法处理冲突的散列表上执行删除操作，只能在被删结点上做删除标记，而不能真正删除结点。实际操作待表格重新整理时在进行——称为惰性删除

3、公共溢出区法：将哈希表分为基本表和溢出表两部分，凡是和基本表发生冲突的元素，一律填入溢出表

4、再哈希法：这种方法是同时构造多个不同的哈希函数：

Hi=RHi（key）,i=1，2，…，k

当哈希地址 Hi=RH1（key） 发生冲突时，再计算 Hi=RH2（key） ……，直到冲突不再产生。

这种方法不易产生聚集，但增加了计算时间。

hash法查找效率：
我们可以看到，哈希表存储和查找数据的时候分为两步，第一步为将关键字通过哈希函数映射为数组中的索引， 这个过程可以认为是只需要常数时间的。第二步是，如果出现哈希值冲突，如何解决，对于常用的拉链法和线性探测法我们可以讨论得到：

对于拉链法，查找的效率在于链表的长度，一般的我们应该保证长度在m /8~m /2之间，如果链表的长度大于m /2，我们可以缩小链表长度。如果长度在0~M/8时，我们可以扩充链表。

对于线性探测法，需要调整数组长度，但是动态调整数组的大小需要对所有的值从新进行重新散列并插入新的表中。因此，拉链法的查找效率要比线性探测法高。

不管是拉链法还是散列法，这种动态调整链表或者数组的大小以提高查询效率的同时，还应该考虑动态改变链表或者数组大小的成本。散列表长度加倍的插入需要进行大量的探测， 这种均摊成本不能忽略。

此外，hash表的查找效率还和负载因子有关，负载因子即hash表的记录数与哈希表的长度的比值，一般为0.7左右。冲突性的概率与负载因子的大小成正比，因此负载因子越大，查找效率越低。

几种数据结构的查找性能的对比

---

Hash能根据散列值直接定位数据的存储地址，设计良好的hash表能在常数级时间下找到需要的数据，但是更适合于内存中的查找。
B+树是一种是一种树状的数据结构，适合做索引，对磁盘数据来说，索引查找是比较高效的

简单谈谈STL中关于HASH的容器

---

C++ STL中，哈希表对应的容器是unordered_map（since C++ 11）。
根据C++ 11标准的推荐，用unordered_map代替hash_map。

这里先来了解一下关于unordered_map的知识。

在STL中，与map对应的数据结构是红黑树，查找时间复杂度是O(logN)不同，unordered_map底层是用hash表存储的，查询时间复杂度是常数级别。但额外空间复杂度则要高出许多。所以对于需要高效率查询的情况，使用unordered_map/hash-map容器。而如果对内存大小比较敏感或者数据存储要求有序的话，则可以用map容器。
unordered_map模板原型：

template < class Key,                                    // unordered_map::key_type
           class T,                                      // unordered_map::mapped_type
           class Hash = hash,                       // unordered_map::hasher
           class Pred = equal_to,                   // unordered_map::key_equal
           class Alloc = allocator< pair<const Key,T> >  // unordered_map::allocator_type
           > class unordered_map;

先来看看unordered_map的简单使用：

#include 
#include 
#include 

int main()
{
 std::unordered_map<std::string, int> months;
 months["january"] = 31;
 months["february"] = 28;
 months["march"] = 31;
 months["april"] = 30;
 months["may"] = 31;
 months["june"] = 30;
 months["july"] = 31;
 months["august"] = 31;
 months["september"] = 30;
 months["october"] = 31;
 months["november"] = 30;
 months["december"] = 31;
 std::cout << "september -> " << months["september"] << std::endl;
 std::cout << "april   -> " << months["april"] << std::endl;
 std::cout << "december -> " << months["december"] << std::endl;
 std::cout << "february -> " << months["february"] << std::endl;
 return 0;
}

unordered_map，[ ] 运算符操作包括
1. 先对 key 算出 hash code
2. 找到这个 hash code 对应的桶
3. 在这个桶里面，遍历去找这个 key 对应的节点
4. 把节点返回
如果找不到节点，并非返回空，而是会创建一个新的空白节点，然后返回这个空白节点，这里估计是受到返回值的约束，因为返回值声明了必须为一个引用，所以总得搞一个东西出来才能有的引用。

同时，unordered_hash内部实现了rehash，而对于rehash的判断，主要是利用一个m_max_load_factor（负载因子）来判断目前的容量需要多少个哈希桶，然后计算如果需要rehash，那么使用素数表来算出新的桶需要多大。need_rehash代码如下：

inline std::pair<bool, std::size_t>
prime_rehash_policy::
need_rehash(std::size_t n_bkt, std::size_t n_elt, std::size_t n_ins) const
{
  if (n_elt + n_ins > m_next_resize)
    {
  float min_bkts = (float(n_ins) + float(n_elt)) / m_max_load_factor;
  if (min_bkts > n_bkt)
    {
      min_bkts = std::max(min_bkts, m_growth_factor * n_bkt);
      const unsigned long* const last = X<>::primes + X<>::n_primes;
      const unsigned long* p = std::lower_bound(X<>::primes, last,
                            min_bkts, lt());
      m_next_resize =
        static_cast<std::size_t>(std::ceil(*p * m_max_load_factor));
      return std::make_pair(true, *p);
    }
  else
    {
      m_next_resize =
        static_cast<std::size_t>(std::ceil(n_bkt * m_max_load_factor));
      return std::make_pair(false, 0);
    }
    }
  else
    return std::make_pair(false, 0);
}

素数表

template<int ulongsize>
    const unsigned long X::primes[256 + 48 + 1] =
    {
      2ul, 3ul, 5ul, 7ul, 11ul, 13ul, 17ul, 19ul, 23ul, 29ul, 31ul,

对于rehash ，一个一个重算，然后重新填进去。

template<typename K, typename V,
     typename A, typename Ex, typename Eq,
     typename H1, typename H2, typename H, typename RP,
     bool c, bool ci, bool u>
  void
  hashtable::
  m_rehash(size_type n)
  {
    node** new_array = m_allocate_buckets(n);
    try
  {
    for (size_type i = 0; i < m_bucket_count; ++i)
      while (node* p = m_buckets[i])
        {
      size_type new_index = this->bucket_index(p, n);
      m_buckets[i] = p->m_next;
      p->m_next = new_array[new_index];
      new_array[new_index] = p;
        }
    m_deallocate_buckets(m_buckets, m_bucket_count);
    m_bucket_count = n;
    m_buckets = new_array;
  }
    catch(...)
  {
    // A failure here means that a hash function threw an exception.
    // We can't restore the previous state without calling the hash
    // function again, so the only sensible recovery is to delete
    // everything.
    m_deallocate_nodes(new_array, n);
    m_deallocate_buckets(new_array, n);
    m_deallocate_nodes(m_buckets, m_bucket_count);
    m_element_count = 0;
    __throw_exception_again;
  }
  }

最后是hash函数：

template<>
  struct Fnv_hash<8>
  {
    static std::size_t
    hash(const char* first, std::size_t length)
    {
  std::size_t result = static_cast<std::size_t>(14695981039346656037ULL);
  for (; length > 0; --length)
    {
      result ^= (std::size_t)*first++;
      result *= 1099511628211ULL;
    }
  return result;
    }
  };

上述使用的为FNV hash，FNV 有分版本，例如 FNV-1 和 FNV-1a，

　　FNV-1形式：

hash = offset_basis
for each octet_of_data to be hashed
hash = hash * FNV_prime
hash = hash xor octet_of_data
return hash

　　FNV-1a形式：

hash = offset_basis
for each octet_of_data to be hashed
hash = hash xor octet_of_data
hash = hash * FNV_prime
return hash

可以看到区别是有两句操作顺序调换，产生FNV-1a的原因是，有些人使用FNV-1a代替FNV-1发现算法离散性或CPU利用效率更好。维基里面说，The small change in order leads to much better avalanche characteristics，即输入的一个非常微小的改动，也会使最终的 hash 结果发生非常巨大的变化，这样的哈希效果被认为是更好的。
可以看到上述hash table用的就是 FNV-1a。

hash 容器除了unordered_map之外，还有unordered_set, unordered_multimap, unordered_multiset。实现原理基本相同，具体应用也类似，下面简单说说unordered_set的使用。
unordered_set模板原型

template < class Key,                        // unordered_set::key_type/value_type
           class Hash = hash,           // unordered_set::hasher
           class Pred = equal_to,       // unordered_set::key_equal
           class Alloc = allocator      // unordered_set::allocator_type
           > class unordered_set; 

可以看到与unordered_map基本一致，区别与hash_map和hash_set相同，即unordered_set只需指定键值的类型，unordered_map需指定键值和实值的类型。
下面是unordered_set常用函数的使用实例：

#include 
#include 

namespace ClassFoo{
void PrintIntDoubleUnOrderedSet(std::unordered_set<int>& m, char* pre) {
    std::unordered_set<int>::iterator it;
    std::cout << pre;
    for ( it = m.begin(); it != m.end(); it++ )
        std::cout << *it << " ";
    std::cout << std::endl;
}
void UnOrderedSetExample1() {
    std::unordered_set<int> foo1;


    // 普通插入
    foo1.insert(1);

    // 带暗示插入，std::pair等价于上述的
    // std::unordered_set::value_type
    foo1.insert(foo1.end(),2);

    // 插入一个范围
    std::unordered_set<int> foo2;
    foo2.insert(3);
    foo2.insert(4);
    foo2.insert(5);
    foo1.insert(foo2.begin(),foo2.end());

    PrintIntDoubleUnOrderedSet(foo1,"插入元素后的foo1：");

    // 查找主键4
    std::unordered_set<int>::iterator it;
    it = foo1.find(4);
    if( it != foo1.end() )
    {
        std::cout << "foo1.find(4)：";
        std::cout << *it << std::endl;
    }

    // 删除上述找到的元素
    if( it != foo1.end() )
    {
        foo1.erase(it);
    }
    PrintIntDoubleUnOrderedSet(foo1,"删除主键为4的元素后的foo1：");

    // 遍历删除主键为2的元素
    for(it = foo1.begin();it != foo1.end();it++)
    {
        //遍历删除主键等于2
        //注意，删除元素会使迭代范围发生变化
        if ( *it == 2 )
        {
            foo1.erase(it);
            break;
        }
    }

    // 内部数据
    std::cout << "bucket_count：" << foo1.bucket_count() << std::endl;
    std::cout << "max_bucket_count：" << foo1.max_bucket_count() << std::endl;
    std::cout << "bucket_size：" << foo1.bucket_size(0) << std::endl;
    std::cout << "load_factor：" << foo1.load_factor() << std::endl;
    std::cout << "max_load_factor：" << foo1.max_load_factor() << std::endl;

    PrintIntDoubleUnOrderedSet(foo1,"删除主键为2的元素后的foo1：");
    foo1.clear();
    PrintIntDoubleUnOrderedSet(foo1,"清空后的foo1：");
}
}
int main( )
{
    ClassFoo::UnOrderedSetExample1();
    return 0;
}

---

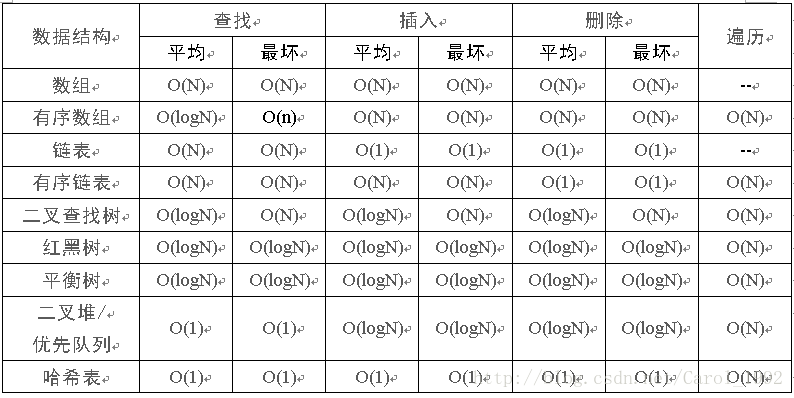
最后，附上常用数据结构的查找、插入、删除等的时间复杂度

参考：
http://blog.csdn.net/v_july_v/article/details/6256463
http://www.cplusplus.com/reference/unordered_set/unordered_set/
《数据结构与算法——C语言描述》