【算法编程】矩阵打印、旋转和查找
一、转圈打印
1、题目描述
给定一个整型矩阵 matrix,请按照转圈的方式打印它。
例如:
[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ] \left[ \begin{matrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{matrix} \right] ⎣⎢⎢⎡15913261014371115481216⎦⎥⎥⎤
打印结果为:1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10
要求:额外空间复杂度为O(1)
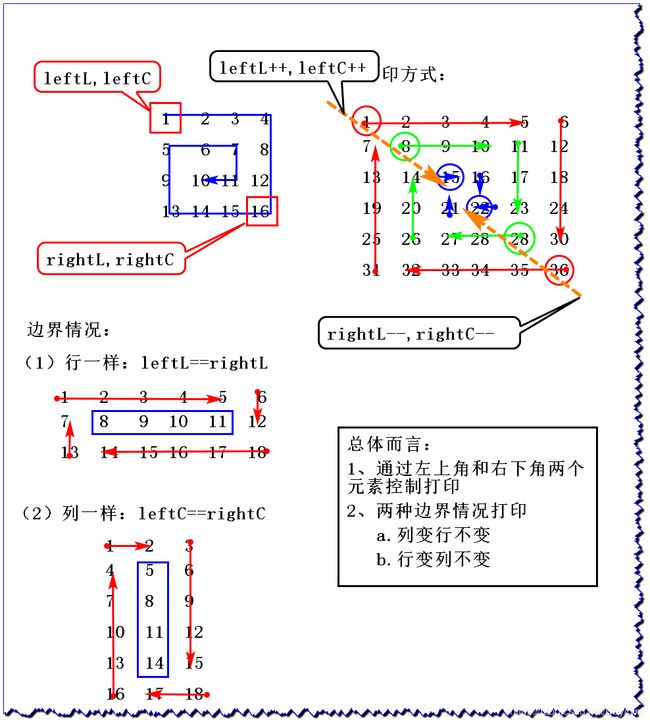
2、图解
3、Java代码
package day02;
public class Code07_PrintMatrixSpiralOrder {
public static void printMatrix(int[][] matrix) {
int leftL = 0; //左行
int leftC = 0; //左列
int rightL = matrix.length - 1; //右行
int rightC = matrix[0].length - 1; //右列
while(leftL <= rightL && leftC <= rightC) {
printEdge(matrix, leftL++, leftC++, rightL--, rightC--);
}
}
public static void printEdge(int[][] m, int lL, int lC, int rL, int rC) {
if(lL == rL) { //边界情况一
for(int i = lC; i <= rC; i++) {
System.out.print(m[lL][i] + " ");
}
}else if(lC == rC) { //边界情况二
for(int i = lL; i <= rL; i++) {
System.out.print(m[i][lC] + " ");
}
}else { //转圈
int curlL = lL;
int curlC = lC;
while(curlC != rC) {
System.out.print(m[lL][curlC] + " ");
curlC++;
}
while(curlL != rL) {
System.out.print(m[curlL][rC] + " ");
curlL++;
}
while(curlC != lC) {
System.out.print(m[rL][curlC] + " ");
curlC--;
}
while(curlL != lL) {
System.out.print(m[curlL][lC] + " ");
curlL--;
}
}
}
public static void main(String[] args) {
int[][] matrix = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 } };
printMatrix(matrix);
}
}
二、旋转正方形矩阵
1、题目描述
给定一个整型正方形矩阵matrix,请把该矩阵调整成顺时针旋转90度的样子
例如:
[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ] \left[ \begin{matrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{matrix} \right] ⎣⎢⎢⎡15913261014371115481216⎦⎥⎥⎤
结果为:
[ 13 9 5 1 14 10 6 2 15 11 7 3 16 12 8 4 ] \left[ \begin{matrix} 13 & 9 &5 &1 \\ 14 &10 &6 &2 \\ 15 &11 &7 &3 \\ 16 &12& 8 &4 \end{matrix} \right] ⎣⎢⎢⎡13141516910111256781234⎦⎥⎥⎤
要求:额外空间复杂度为O(1)
2、图解
3、Java代码
package day02;
public class Code08_RotateMatrix {
public static void rotate(int[][] matrix) {
int leftL = 0;
int leftC = 0;
int rightL = matrix.length - 1;
int rightC = matrix[0].length - 1;
while (leftL < rightL) {
rotateEdge(matrix, leftL++, leftC++, rightL--, rightC--);
}
}
public static void rotateEdge(int[][] m, int lL, int lC, int rL, int rC) {
int times = rC - lC; //每圈需要交换几次
int tmp = 0;
for (int i = 0; i != times; i++) { //每次交换4个点
tmp = m[lL][lC + i];
m[lL][lC + i] = m[rL - i][lC];
m[rL - i][lC] = m[rL][rC - i];
m[rL][rC - i] = m[lL + i][rC];
m[lL + i][rC] = tmp;
}
}
public static void printMatrix(int[][] matrix) {
for (int i = 0; i != matrix.length; i++) {
for (int j = 0; j != matrix[0].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
{ 13, 14, 15, 16 } };
printMatrix(matrix);
rotate(matrix);
System.out.println("=========");
printMatrix(matrix);
}
}
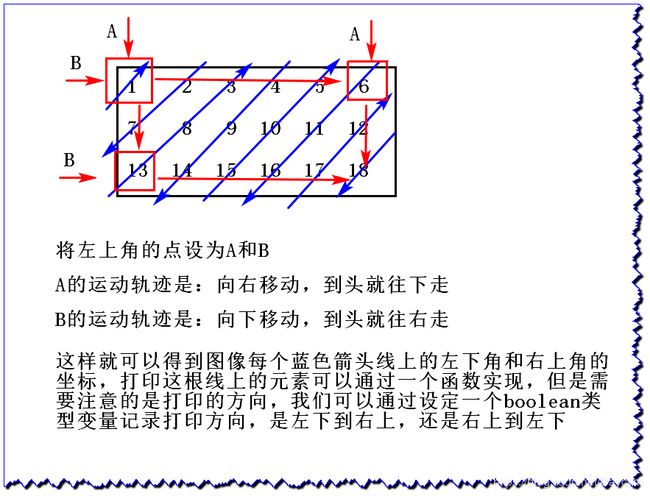
三、“之”字型打印
1、题目描述
给定一个矩阵matrix,按照“之”字形的方式打印这个矩阵
例如:
[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ] \left[ \begin{matrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{matrix} \right] ⎣⎢⎢⎡15913261014371115481216⎦⎥⎥⎤
结果为:1 2 5 9 6 3 4 7 10 13 14 11 8 12 15 16
要求:额外空间复杂度为O(1)
2、图解
3、Java代码
package day02;
public class Code09_ZiPrintMatrix {
public static void ziPrintMatrix(int[][] matrix) {
int aL = 0;
int aC = 0;
int bL = 0;
int bC = 0;
int endL = matrix.length - 1;
int endC = matrix[0].length - 1;
boolean fromUp = false;
while(aL != endL + 1) {
printElement(matrix, aL, aC, bL, bC, fromUp);
//下面两行不能换,换了就更新了aC,下面在判断aC == endC就不是原先的了
aL = aC == endC ? aL + 1 : aL; //a到头,行+1,否则行不变
aC = aC == endC ? aC : aC + 1; //a到头,列不变,否则列+1
//下面两行同样
bC = bL == endL ? bC + 1 : bC; //b到头,列+1,否则列不变
bL = bL == endL ? bL : bL + 1; //b到头,行不变,否则行+1
fromUp = !fromUp; //方向改变
}
System.out.println();
}
public static void printElement(int[][] m, int aX, int aY, int bX, int bY, boolean f) {
if(f) {
while(aX != bX + 1) {
System.out.print(m[aX++][aY--] + " ");
}
}else {
while(bX != aX - 1) {
System.out.print(m[bX--][bY++] + " ");
}
}
}
public static void main(String[] args) {
int[][] matrix = { { 1, 2, 3, 4, 5, 6 },
{ 7, 8, 9, 10, 11, 12 },
{ 13, 14, 15, 16, 17, 18 } };
ziPrintMatrix(matrix);
}
}
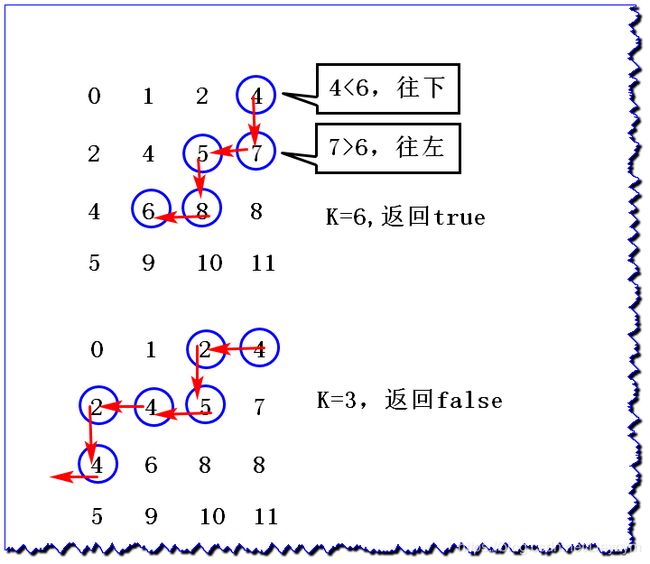
四、在行列都排好序的矩阵中找数
1、题目描述
给定一个有 N*M 的整型矩阵 matrix 和一个整数 K, matrix 的每一行和每一 列都是排好序的。实现一个函数,判断 K是否在 matrix 中。
例如:
[ 0 1 2 5 2 3 4 7 4 4 4 8 5 7 7 9 ] \left[ \begin{matrix} 0 & 1 & 2 & 5 \\ 2 & 3 & 4 & 7 \\ 4 & 4 & 4 & 8 \\ 5 & 7& 7& 9 \end{matrix} \right] ⎣⎢⎢⎡0245134724475789⎦⎥⎥⎤
如果 K 为7,返回 true ;如果 K 为 6,返回 false
要求:时间复杂度为O(N+M),额外空间复杂度为O(1)
2、图解
待查找的数大于当前数,向下搜索;小于当前数,向左搜索;等于即找到了
到边界表示没找到
3、Java代码
package day02;
public class Code10_FindNumInMatrix {
public static boolean isContains(int[][] matrix, int k) {
int row = 0;
int col = matrix[0].length - 1;
while(row < matrix.length && col > -1) {
if(matrix[row][col] == k) {
return true;
}else if(matrix[row][col] > k) {
col--;
}else{
row++;
}
}
return false;
}
public static void main(String[] args) {
int[][] matrix = new int[][] {
{ 0, 1, 2, 3, 4, 5, 6 },
{ 10, 12, 13, 15, 16, 17, 18 },
{ 23, 24, 25, 26, 27, 28, 29 },
{ 44, 45, 46, 47, 48, 49, 50 },
{ 65, 66, 67, 68, 69, 70, 71 },
{ 96, 97, 98, 99, 100, 111, 122 },
{ 166, 176, 186, 187, 190, 195, 200 },
{ 233, 243, 321, 341, 356, 370, 380 }
};
System.out.println(isContains(matrix, 233));
System.out.println(isContains(matrix, 113));
}
}