2019第十届蓝桥杯省赛C/C++B组题解

题目:

链接: https://pan.baidu.com/s/1Q9wEv_mQh-Ovr5uiWY0JWA 提取码: ph47

一、组队

作为篮球队教练，你需要从以下名单中选出 1 号位至 5 号位各一名球员，组成球队的首发阵容。
每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1 号位至 5 号位的评分之和最大可能是多少？

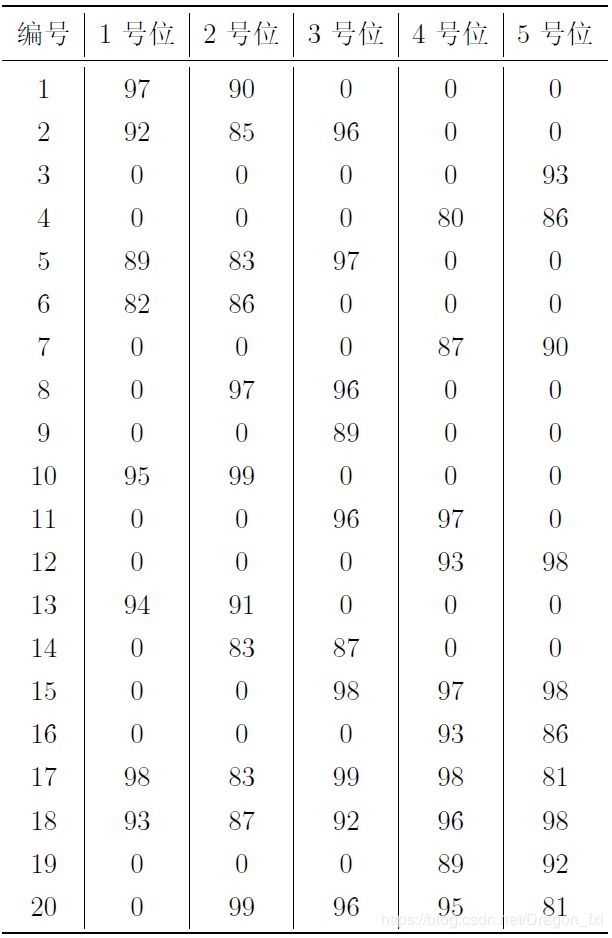
1 97 90 0 0 0
2 92 85 96 0 0
3 0 0 0 0 93
4 0 0 0 80 86
5 89 83 97 0 0
6 82 86 0 0 0
7 0 0 0 87 90
8 0 97 96 0 0
9 0 0 89 0 0
10 95 99 0 0 0
11 0 0 96 97 0
12 0 0 0 93 98
13 94 91 0 0 0
14 0 83 87 0 0
15 0 0 98 97 98
16 0 0 0 93 86
17 98 83 99 98 81
18 93 87 92 96 98
19 0 0 0 89 92
20 0 99 96 95 81

答案: 490

二、年号字串

小明用字母A 对应数字1，B 对应2，以此类推，用Z 对应26。对于27以上的数字，小明用两位或更长位的字符串来对应，例如AA 对应27，AB 对应28，AZ 对应52，LQ 对应329。
请问2019 对应的字符串是什么？

代码：

#include 
using namespace std;
//702 --> ZZ
//703 --> AAA
//18278 --> ZZZ
//18279 --> AAAA
void dfs(int N) {
    //并不是26进制哟
    if (N > 26) dfs((N - 1) / 26);
    putchar('A' + (N - 1) % 26);
}
int main() {
    int N;
    while (cin >> N) {
        dfs(N); cout << endl;
    }
    return 0;
}

答案: BYQ

三、数列求值

给定数列1, 1, 1, 3, 5, 9, 17, …，从第4 项开始，每项都是前3 项的和。求
第20190324 项的最后4 位数字。

思路：

改一下求斐波那契数列的代码就行了。（当然不用数组也是可以的）

代码：

#include 
using namespace std;
const int MAXN = 30000000;
int a[MAXN];
int main() {
    int N = 20190324;
    a[1] = a[2] = a[3] = 1;
    for (int i = 4; i <= N; ++i)
        a[i] = (a[i - 1] + a[i - 2] + a[i - 3]) % 10000;
    printf("%d\n", a[N]);
    return 0;
}

补充：（O(1)空间复杂度）

#include 
using namespace std;
int main() {
    int a = 1, b = 1, c = 1;
    int N = 20190324;   //scanf("%d", &N);
    for (int i = 4; i <= N; ++i) {
        int t = (a + b + c) % 10000;
        c = b; 
        b = a;
        a = t;
    }
    printf("%d\n", a);
    return 0;
}

答案: 4659

四、数的分解

把2019 分解成3 个各不相同的正整数之和，并且要求每个正整数都不包含数字 2 和 4，一共有多少种不同的分解方法？
注意交换3个整数的顺序被视为同一种方法，例如1000+1001+18 和 1001+1000+18 被视为同一种。

思路：

让i < j < k, 然后判断i, j, k是否含2和4就行了

代码：

#include 
using namespace std;
bool isOK(int x) {
    for (/* */; x > 0; x /= 10)
        if (x % 10 == 2 || x % 10 == 4) return false;
    return true;
}
int main() {
    int N = 2019;
    int cnt = 0;
    for (int i = 1; i < N / 3; ++i)
        if (isOK(i))
            //k = N - i - j > j
            for (int j = i + 1; N - i - j > j; ++j)
                if (isOK(j) && isOK(N - i - j)) ++cnt;
    cout << cnt << endl;
    return 0;
}

答案: 40785

五、 迷宫

下图给出了一个迷宫的平面图，其中标记为1 的为障碍，标记为0 的为可以通行的地方。

010000
000100
001001
110000

迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这个它的上、下、左、右四个方向之一。
对于上面的迷宫，从入口开始，可以按DRRURRDDDR 的顺序通过迷宫，一共10 步。其中D、U、L、R 分别表示向下、向上、向左、向右走。对于下面这个更复杂的迷宫（30 行50 列），请找出一种通过迷宫的方式，其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。请注意在字典序中D

01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000

思路：

BFS，方向为上左右下，这样的方向能使得到的路径字典序最小。
输出路径使用DFS。

代码：

#include 
using namespace std;
const int MAXN = 100, MAXM = 100;
const int f[4] = { 1, 0, 0, -1 };
const int g[4] = { 0, -1, 1, 0 };
const char* s = "DLRU";
char a[MAXN][MAXM];
int r[MAXN][MAXM];
typedef pair<int, int> P;
int N, M;
void print(int x, int y) {
    if (x != 1 || y != 1) {
        int t = r[x][y];
        print(x - f[t], y - g[t]);
        cout << s[t];
    }
}
void solve() {
    queue<P> que; que.push(P(1, 1)); a[1][1] = '1';
    while (!que.empty()) {
        int x = que.front().first, y = que.front().second; que.pop();
        for (int i = 0; i < 4; ++i) {
            int nx = x + f[i], ny = y + g[i];
            if (a[nx][ny] == '0') {
                a[nx][ny] = '1';
                que.push(P(nx, ny));
                r[nx][ny] = i;
            }
        }
    }
    print(N, M);
}
int main() {
    //cin >> N >> M;
    N = 30, M = 50;
    memset(a, '1', sizeof(a));
    for (int i = 1; i <= N; ++i)
        scanf("%s", &a[i][1])/*, a[i][N + 1] = '1'*/;
    solve();
    return 0;
}

答案: DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR

六、特别数的和

小明对数位中含有 2、0、1、9 的数字很感兴趣（不包括前导0），在1 到 40 中这样的数包括1、2、9、10 至 32、39 和 40，共 28 个，他们的和是 574。请问，在 1 到n 中，所有这样的数的和是多少？

【输入格式】
输入一行包含两个整数n。

【输出格式】
输出一行，包含一个整数，表示满足条件的数的和。

【样例输入】
40

【样例输出】
574

【评测用例规模与约定】
对于20% 的评测用例，$1\le n\le 10$。
对于50% 的评测用例，$1\le n\le 100$。
对于80% 的评测用例，$1\le n\le 1000$。
对于所有评测用例，$1\le n\le 10000$。

思路:

枚举。时间复杂度: $O(N)$

参考代码:

#include 
using namespace std;
int N;
bool isOK(int x) {
    for (/* */; x > 0; x /= 10) {
        int t = x % 10;
        if (t % 10 == 2 || t % 10 == 0 || t % 10 == 1 || t % 10 == 9)
            return true;
    }
    return false;
}
int main() {
    cin >> N;
    int ret = 0;
    for (int i = 1; i <= N; ++i)
        if (isOK(i)) ret += i;
    cout << ret << endl;
    return 0;
}

七、完全二叉树的权值

给定一棵包含N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是$A_1,A_2,...,A_N$，如下图所示：
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。
注：根的深度是1。

【输入格式】
第一行包含一个整数N。
第二行包含N 个整数$A_1,A_2,...,A_N$ 。

【输出格式】
输出一个整数代表答案。

【样例输入】
7
1 6 5 4 3 2 1

【样例输出】
2
【评测用例规模与约定】
对于所有评测用例，$1\le N\le 100000$，$-100000\le Ai\le 100000$。

思路:

枚举。时间复杂度: $O(N)$

注意: 最大和可能为负数

数据1:

3
-100000 -99999 -99999

答案:

1

数据2:

3
-100000 -49999 -49999

答案:

2

参考代码:

#include 
using namespace std;
const int MAXN = 100000;
int N, a[MAXN + 1];
int main() {
    scanf("%d", &N);
    for (int i = 1; i <= N; ++i)
        scanf("%d", a + i);
    long long m = -MAXN;    //m一定要设为-MAXN(或更小)
    int ans = 1;            //答案默认为1
    for (int i = 1; (1 << (i - 1)) <= N; ++i) {
        long long t = 0;
        for (int j = 1 << (i - 1); j < (1 << i) && j <= N; ++j)
            t += a[j];
        if (m < t) {
            m = t;
            ans = i;
        }
    }
    cout << ans << endl;
    return 0;
}

八、等差数列

数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列，只记得其中N 个整数。
现在给出这N 个整数，小明想知道包含这N 个整数的最短的等差数列有几项？
【输入格式】
输入的第一行包含一个整数N。
第二行包含N 个整数$A_1,A_2,...,A_N$。(注意$A_1$ ~ $A_N$ 并不一定是按等差数列中的顺序给出)

【输出格式】
输出一个整数表示答案。

【样例输入】
5
2 6 4 10 20

【样例输出】
10

【样例说明】
包含2、6、4、10、20 的最短的等差数列是2、4、6、8、10、12、14、16、18、20。

【评测用例规模与约定】
对于所有评测用例，$2\le N\le 100000$，$0\le Ai\le 10^9$。

思路:

排序+遍历求两数之差的gcd。时间复杂度: $O(NlogN)$

注意: d=0为常数数列, 答案为N

参考代码:

#include 
using namespace std;
const int MAXN = 100000;
int N, a[MAXN];
int gcd(int a, int b) {
    return !b ? a : gcd(b, a % b);
}
int main() {
    scanf("%d", &N);
    for (int i = 0; i < N; ++i)
        scanf("%d", a + i);
    sort(a, a + N);
    int d = a[1] - a[0];
    if (d == 0) return printf("%d\n", d), 0;    //d=0为常数数列，这个有点坑呀
    for (int i = 2; i < N; ++i)
        d = gcd(d, a[i] - a[i - 1]);
    printf("%d\n", (a[N - 1] - a[0]) / d + 1);
    return 0;
}

九、后缀表达式

相似题 (N=0, 感觉表达式这题应该是改编的): Slime

给定N 个加号、M 个减号以及N + M + 1 个整数$A_1,A_2,...,A_{M+N+1}$，小明想知道在所有由这 N 个加号、M 个减号以及 N + M +1 个整数凑出的合法的后缀表达式中，结果最大的是哪一个？
请你输出这个最大的结果。
例如使用1 2 3 + -，则“2 3 + 1 -” 这个后缀表达式结果是4，是最大的。

【输入格式】
第一行包含两个整数N 和M。
第二行包含N + M + 1 个整数$A_1,A_2,...,A_{M+N+1}$。

【输出格式】
输出一个整数，代表答案。

【样例输入】
1 1
1 2 3
【样例输出】
4

【评测用例规模与约定】
对于所有评测用例，$1\le N,M\le 100000$，$-10^9\le A_i\le 10^9$。

思路:

这题还是有点坑呀，以为直接贪心就能解决的。。。还是想的太简单了呀。

之前的代码写错了，有空再补思路。

时间复杂度: $O(N)$

参考代码:

#include 
using namespace std;
const int MAXN = 100000;
const int MAXM = 100000;
const int INF = 0x3f3f3f3f;
int a[MAXN + MAXM + 1], N, M;
int main() {
    scanf("%d%d", &N, &M);
    int mini = INF, maxi = -INF;
    for (int i = 0; i <= N + M; ++i) {
        scanf("%d", a + i);
        mini = min(a[i], mini);
        maxi = max(a[i], maxi);
    }
    long long ret = 0;
    if (M) {
        for (int i = 0; i <= N + M; ++i)
            ret += abs(a[i]);
        if (mini > 0) ret -= mini * 2;
        if (maxi < 0) ret += maxi * 2;
    }
    else for (int i = 0; i <= N + M; ++i)
        ret += a[i];
    cout << ret << endl;
    return 0;
}

赛后总结:

前5题应该没什么问题，可惜的是7-9三个大题都太大意了。以后还是得留点时间检查大题呀，总好过做一题不会的大题。。。省一感觉还是有点不稳呀。