【python数据挖掘课程】十九.鸢尾花数据集可视化、线性回归、决策树花样分析
1.鸢尾花数据集可视化分析
2.线性回归分析鸢尾花花瓣长度和宽度的关系
3.决策树分析鸢尾花数据集
4.Kmeans聚类分析鸢尾花数据集
本篇文章为基础性文章,希望对你有所帮助,如果文章中存在错误或不足支持,还请海涵~这也是自己书籍几章的内容,同时,推荐大家阅读我以前的文章了解基础知识。自己真的太忙了,只能挤午休或深夜的时间学习新知识,周五深夜写下这篇文章,内心非常享受。
前文参考:
【Python数据挖掘课程】一.安装Python及爬虫入门介绍
【Python数据挖掘课程】二.Kmeans聚类数据分析及Anaconda介绍
【Python数据挖掘课程】三.Kmeans聚类代码实现、作业及优化
【Python数据挖掘课程】四.决策树DTC数据分析及鸢尾数据集分析
【Python数据挖掘课程】五.线性回归知识及预测糖尿病实例
【Python数据挖掘课程】六.Numpy、Pandas和Matplotlib包基础知识
【Python数据挖掘课程】七.PCA降维操作及subplot子图绘制
【Python数据挖掘课程】八.关联规则挖掘及Apriori实现购物推荐
【Python数据挖掘课程】九.回归模型LinearRegression简单分析氧化物数据
【python数据挖掘课程】十.Pandas、Matplotlib、PCA绘图实用代码补充
【python数据挖掘课程】十一.Pandas、Matplotlib结合SQL语句可视化分析
【python数据挖掘课程】十二.Pandas、Matplotlib结合SQL语句对比图分析
【python数据挖掘课程】十三.WordCloud词云配置过程及词频分析
【python数据挖掘课程】十四.Scipy调用curve_fit实现曲线拟合
【python数据挖掘课程】十五.Matplotlib调用imshow()函数绘制热图
【python数据挖掘课程】十六.逻辑回归LogisticRegression分析鸢尾花数据
【python数据挖掘课程】十七.社交网络Networkx库分析人物关系(初识篇)
【python数据挖掘课程】十八.线性回归及多项式回归分析四个案例分享
一. 鸢尾花数据集介绍
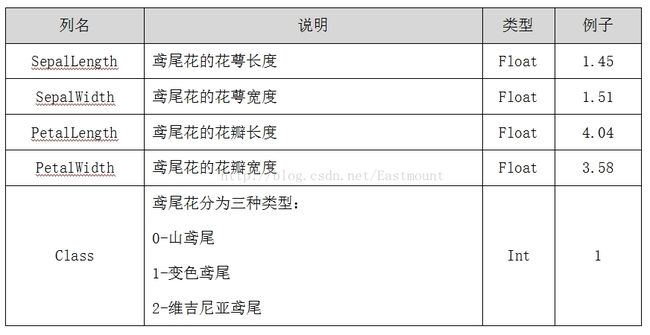
在做数据分析过程中,数据集通常可以来源于自己的需求,也可以从网上寻找公开的数据集,也可以随机生成一个数据集,本章采用Python的Sklearn机器学习库中自带的数据集——鸢尾花数据集。简单分析数据集之间特征的关系图,根据花瓣长度、花瓣宽度、花萼长度、花萼宽度四个特征进行绘图。
Iris plants data set数据集可以从KEEL dataset数据集网站获取,也可以直接从Sklearn.datasets机器学习包得到。数据集共包含4个特征变量、1个类别变量,共有150个样本。类别变量分别对应鸢尾花的三个亚属,分别是山鸢尾 (Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)。
通过sklearn.datasets扩展包中的load_iris()函数导入鸢尾花数据集,该Iris中有两个属性,分别是:iris.data和iris.target。data里是一个矩阵,每一列代表了萼片或花瓣的长宽,一共4列,每一列代表某个被测量的鸢尾植物,一共采样了150条记录。代码如下:
#导入数据集iris
from sklearn.datasets import load_iris
#载入数据集
iris = load_iris()
#输出数据集
print iris.data 输出如下所示内容:
[[ 5.1 3.5 1.4 0.2]
[ 4.9 3. 1.4 0.2]
[ 4.7 3.2 1.3 0.2]
[ 4.6 3.1 1.5 0.2]
[ 5. 3.6 1.4 0.2]
....
[ 6.7 3. 5.2 2.3]
[ 6.3 2.5 5. 1.9]
[ 6.5 3. 5.2 2. ]
[ 6.2 3.4 5.4 2.3]
[ 5.9 3. 5.1 1.8]] target是一个数组,存储了data中每条记录属于哪一类鸢尾植物,数组长度是150,数组元素的值因为共有3类鸢尾植物,所以不同值只有3个。种类:
Iris Setosa(山鸢尾)
Iris Versicolour(杂色鸢尾)
Iris Virginica(维吉尼亚鸢尾)
代码如下:
#输出真实标签
print iris.target
print len(iris.target)
#150个样本 每个样本4个特征
print iris.data.shape 输出结果如下:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
150
(150L, 4L) 可以看到,类标共分为三类,前面50个类标位0,中间50个类标位1,后面为2。下面讲解另一种导入鸢尾花数据集的方法,这里是从某一网页导入数据,但是如果网页打不开很可能就导入不了,但也普及下方法。代码如下:
import pandas
#导入数据集iris
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = pandas.read_csv(url, names=names) #读取csv数据
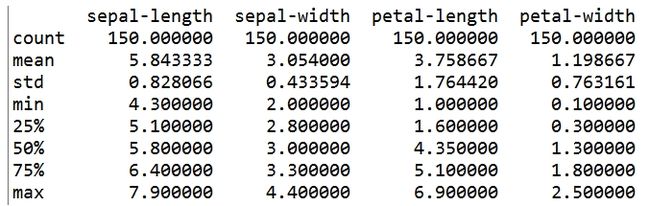
print(dataset.describe()) 输出如图所示,鸢尾花(iris)是数据挖掘常用到的一个数据集,包含150种鸢尾花的信息,每50种取自三个鸢尾花种之一(setosa,versicolour或virginica)。每个花的特征用下面的5种属性描述萼片长度(Sepal.Length)、萼片宽度(Sepal.Width)、花瓣长度(Petal.Length)、花瓣宽度(Petal.Width)、类(Species)。
可以看到如下结果,分别表示4个属性的样本值、均值、标准误、最小值、25%分位数、中位数、75%分位数、最大值。接下来主介绍可视化操作,调用Pandas扩展包读取数据并绘制相关图形。
二. 可视化分析鸢尾花
数据可视化可以更好地了解数据,主要调用Pandas扩展包进行绘图操作。
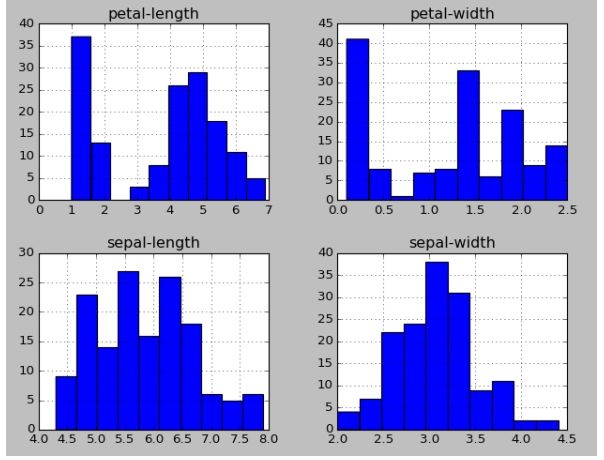
首先绘制直方图,直观的表现花瓣、花萼的长和宽特征的数量,纵坐标表示汇总的数量,横坐标表示对应的长度。
import pandas
#导入数据集iris
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = pandas.read_csv(url, names=names) #读取csv数据
print(dataset.describe())
#直方图 histograms
dataset.hist()
接下来通过dataset.plot()绘制散点图,这里设置三个参数,显示的x坐标、y坐标和设置绘图种类。
import pandas
#导入数据集iris
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = pandas.read_csv(url, names=names) #读取csv数据
print(dataset.describe())
dataset.plot(x='sepal-length', y='sepal-width', kind='scatter')
通过dataset.plot(kind='kde')绘制KDE图,KDE图也被称作密度图(Kernel Density Estimate,核密度估计)。
import pandas
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = pandas.read_csv(url, names=names) #读取csv数据
print(dataset.describe())
dataset.plot(kind='kde')通过四条曲线反映四个特征的变化情况。
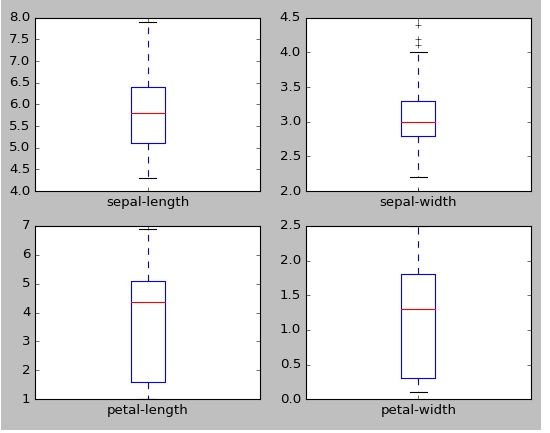
设置dataset.plot()函数的类型kind='box'绘制箱图,在这里注意各个箱形图的纵坐标(y轴)的刻度是不同的,有明显的区分,因此可以看到,各变量表示的属性是有区分的。代码如下:
import pandas
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = pandas.read_csv(url, names=names) #读取csv数据
print(dataset.describe())
dataset.plot(kind='kde')
dataset.plot(kind='box', subplots=True, layout=(2,2),
sharex=False, sharey=False)接下来调用radviz()函数、andrews_curves()函数和parallel_coordinates()函数绘制图形,这里选择petal-length特征,代码如下所示:
import pandas
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = pandas.read_csv(url, names=names)
from pandas.tools.plotting import radviz
radviz(dataset, 'class')
from pandas.tools.plotting import andrews_curves
andrews_curves(dataset, 'class')
from pandas.tools.plotting import parallel_coordinates
parallel_coordinates(dataset, 'class')最后补充散点图矩阵,这有助于发现变量之间的结构化关系,散点图代表了两变量的相关程度,如果呈现出沿着对角线分布的趋势,说明它们的相关性较高。
import pandas
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
dataset = pandas.read_csv(url, names=names)
from pandas.tools.plotting import scatter_matrix
scatter_matrix(dataset, alpha=0.2, figsize=(6, 6), diagonal='kde')三. 线性回归分析鸢尾花
该部分主要采用线性回归算法对鸢尾花的特征数据进行分析,预测花瓣长度、花瓣宽度、花萼长度、花萼宽度四个特征之间的线性关系。该部分的核心代码及步骤解释如下:
第一步 导入鸢尾花数据集并获取前两列数据,分别存储至x和y数组
from sklearn.datasets import load_iris
hua = load_iris()
#获取花瓣的长和宽
x = [n[0] for n in hua.data]
y = [n[1] for n in hua.data]但由于存储的x、y变量为list类型,而使用线性回归fit()函数训练时,需要转换为数组array类型,则使用如下代码进行转换。
import numpy as np #转换成数组
x = np.array(x).reshape(len(x),1)
y = np.array(y).reshape(len(y),1)
第二步 导入Sklearn机器学习扩展包中线性回归模型,然后进行训练和预测
from sklearn.linear_model import LinearRegression
clf = LinearRegression()
clf.fit(x,y)
pre = clf.predict(x)
第三步 调用Matplotlib扩展包并绘制相关图形
#第三步 画图
import matplotlib.pyplot as plt
plt.scatter(x,y,s=100)
plt.plot(x,pre,"r-",linewidth=4)
for idx, m in enumerate(x):
plt.plot([m,m],[y[idx],pre[idx]], 'g-')
plt.show()经过上述三个步骤,一个简单的鸢尾花线性回归方程就讲解完毕。完整代码如下:
from sklearn.datasets import load_iris
hua = load_iris()
#获取花瓣的长和宽
x = [n[0] for n in hua.data]
y = [n[1] for n in hua.data]
import numpy as np #转换成数组
x = np.array(x).reshape(len(x),1)
y = np.array(y).reshape(len(y),1)
from sklearn.linear_model import LinearRegression
clf = LinearRegression()
clf.fit(x,y)
pre = clf.predict(x)
#第三步 画图
import matplotlib.pyplot as plt
plt.scatter(x,y,s=100)
plt.plot(x,pre,"r-",linewidth=4)
for idx, m in enumerate(x):
plt.plot([m,m],[y[idx],pre[idx]], 'g-')
plt.show()输出如下图所示,同时绘制了所有散点图到直线的距离。其中散点图为鸢尾花真实的花萼长度和花萼宽度关系,红色直线为预测的线性回归方程,即预测结果。
最后对该算法进行评估,主要是计算其线性回归方程,代码如下:
print u"系数", clf.coef_
print u"截距", clf.intercept_
print np.mean(y-pre)**2
# 系数 [[-0.05726823]]
# 截距 [ 3.38863738]
# 1.91991214088e-31假设现在存在一个花萼长度为5.0的花,需要预测其花萼宽度,则使用该已经训练好的线性回归模型进行预测,其结果应为[3.10229621]。
print clf.predict([[5.0]])
# [[ 3.10229621]]四. 决策树分析鸢尾花
Sklearn机器学习包中,决策树实现类是DecisionTreeClassifier,能够执行数据集的多类分类。输入参数为两个数组X[n_samples,n_features]和y[n_samples],X为训练数据,y为训练数据的标记数据。
DecisionTreeClassifier构造方法为:
sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best'
,max_depth=None, min_samples_split=2, min_samples_leaf=1
,max_features=None, random_state=None, min_density=None
,compute_importances=None, max_leaf_nodes=None)鸢尾花数据集使用决策树的代码如下:
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
clf = DecisionTreeClassifier()
clf.fit(iris.data, iris.target)
print clf
predicted = clf.predict(iris.data)
#获取花卉两列数据集
X = iris.data
L1 = [x[0] for x in X]
print L1
L2 = [x[1] for x in X]
print L2
import numpy as np
import matplotlib.pyplot as plt
plt.scatter(L1, L2, c=predicted, marker='x') #cmap=plt.cm.Paired
plt.title("DTC")
plt.show() 输出结果如下所示,可以看到分位三类,分别代表数据集三种鸢尾植物。
上面的代码predicted = clf.predict(iris.data)是对整个的数据集进行决策树分析,而真是的分类分析,需要把一部分数据集作为训练,一部分作为预测,这里使用70%的训练,30%的进行预测,其中70%的训练集为0-40、50-90、100-140行,30%的预测集40-50、90-100、140-150行。同时输出准确率、召回率等,优化后的完整代码如下所示:
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
#训练集
train_data = np.concatenate((iris.data[0:40, :], iris.data[50:90, :], iris.data[100:140, :]), axis = 0)
train_target = np.concatenate((iris.target[0:40], iris.target[50:90], iris.target[100:140]), axis = 0)
#测试集
test_data = np.concatenate((iris.data[40:50, :], iris.data[90:100, :], iris.data[140:150, :]), axis = 0)
test_target = np.concatenate((iris.target[40:50], iris.target[90:100], iris.target[140:150]), axis = 0)
#训练
clf = DecisionTreeClassifier()
clf.fit(train_data, train_target)
predict_target = clf.predict(test_data)
print predict_target
#预测结果与真实结果比对
print sum(predict_target == test_target)
#输出准确率 召回率 F值
from sklearn import metrics
print(metrics.classification_report(test_target,predict_target))
print(metrics.confusion_matrix(test_target,predict_target))
X = test_data
L1 = [n[0] for n in X]
print L1
L2 = [n[1] for n in X]
print L2
import numpy as np
import matplotlib.pyplot as plt
plt.scatter(L1, L2, c=predict_target, marker='x') #cmap=plt.cm.Paired
plt.title("DecisionTreeClassifier")
plt.show()输出结果如下:
[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2]
30
precision recall f1-score support
0 1.00 1.00 1.00 10
1 1.00 1.00 1.00 10
2 1.00 1.00 1.00 10
avg / total 1.00 1.00 1.00 30
[[10 0 0]
[ 0 10 0]
[ 0 0 10]] 绘制图形如下所示:
五. Kmeans聚类分析鸢尾花
KMeans聚类鸢尾花的代码如下,它则不需要类标(属于某一类鸢尾花),而是根据数据之间的相似性,按照“物以类聚,人以群分”进行聚类。代码如下:
# -*- coding: utf-8 -*-
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
iris = load_iris()
clf = KMeans()
clf.fit(iris.data, iris.target)
print clf
predicted = clf.predict(iris.data)
#获取花卉两列数据集
X = iris.data
L1 = [x[0] for x in X]
print L1
L2 = [x[1] for x in X]
print L2
import numpy as np
import matplotlib.pyplot as plt
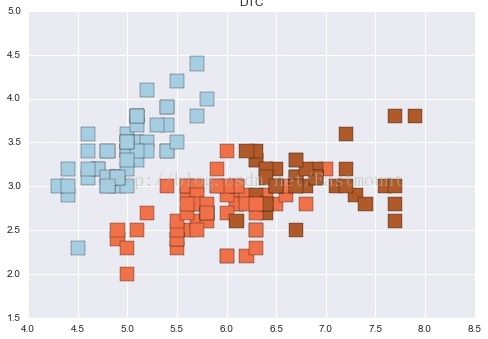
plt.scatter(L1, L2, c=predicted, marker='s',s=200,cmap=plt.cm.Paired)
plt.title("DTC")
plt.show() 希望文章对你有所帮助,尤其是我的学生,如果文章中存在错误或不足之处,还请海涵。
12月了,今年又要结束了,这一年真的成才很多,不是编程,而是做人做事,谢谢她!
再多赞美的语言,都比不上滴滴汗水凝结的成功带来的满足与喜悦,愿你看完这篇文章,能感受到我秀璋的真诚。希望你能从这篇文章中学到一些简单的数据分析知识。
(By:Eastmount 2017-12-01 深夜12点 http://blog.csdn.net/eastmount/ )