《数据结构与算法之美》专栏阅读笔记4——二分查找

找呀找呀找朋友

1、二分查找

二分查找也叫折半查找，是一种针对有序数据集合的查找算法。
原理：押大押小呀？

复杂度分析
2^k = N，O(logn)

适用场景

• 有序数据
• 依赖于顺序表结构，用数组性能最高，因为数组查找的时间复杂度为O(1)，用链表复杂度为O(n) = n/2 + n/4 + …
• 数据量较少或较大都不合适：数据量小，优势不明显（哦。。。），数据量大的情况下，因为要把查找的关键字都放到数组里（数组占用的是连续的内存哦~），贫穷限制了我的发展？

作业~【求一个数的平方根，精确到小数点后6位】
看到题目的第一反应是，啥？啥叫平方根？精确到小数点后是几个意思？小数点单独算？（信号处理专业中数学最差的说的大概就是我……）反应过来啥叫平方根后，脑补了一下小数点的限制的方法，然后就……想起来作者之前的忠告：

public static double sqrt1(double value) {
        if (value <= 0)
            return 0;

        double eps = 1e-7;
        double left,right,mid;
        left = 0;
        right = value;
        while (Math.abs(left*left - value) > eps) {
            mid = (left + right) / 2;
            if (mid * mid < value) {
                left = mid;
            } else {
                right = mid;
            }
        }
        return left;
    }

强迫症般纠结的我发现36的平方根居然不是6的时候，面临崩溃，才发现不是我的锅。
科普一下牛顿-拉弗森法（喜欢讲着么清楚的文~）

用来求平方根的话，公式大概就是：

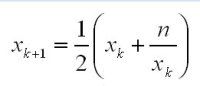
实现就是

public static double sqrt2(double value) {
        if (value <= 0)
            return 0;

        double c = value;
        double old = 0.0;
        double eps = 1e-7;
        while (Math.abs(old - c) > eps) {
            old = c;
            c = (c + value/c) / 2;
        }
        return c;
    }

36的平方根就是6了呢~
（还是学数学的厉害呢~）

2、变形的二分查找

常见的四个变形问题

• 查找第一个值等于给定值的元素
• 查找最后一个值等于给定值的元素
• 查找第一个大于等于给定值的元素
• 查找最后一个小于等于给定值的元素

2.1、查找第一个、最后一个值等于给定值的元素

下面是查找第一个等于给定值的元素的实现代码。
原始写法

public static int firstEqual(int[] values, int target) {
        int left = 0;
        int right = values.length - 1;
        int mid = left + ((right - left) >> 1);
        while (left < right) {
            if (values[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
            mid = left + ((right - left) >> 1);
        }

        while (mid >= 0 && values[mid] == target) {
            mid--;
        }

        return mid+1;
    }

跟作者给出来的说是不好理解的写法差不多的呢，就是看到下面的while之后就发现我可能是瞬间脑抽了。不过看到“标准答案”后也明白了这样好像更优雅，同时也说明我虽然“不小心”处理了等于的情况，但是没有理解等于的情况交给右边界其实可以保证左边界收缩到第一个值的位置。

int left = 0;
        int right = values.length - 1;
        int mid = left + ((right - left) >> 1);
        while (left < right) {
            if (values[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
            mid = left + ((right - left) >> 1);
        }
        if (left < values.length && values[left] == target)
            return left;
        return -1;

另外一种更好理解的写法，其实是把等于的情况单独拿出来显式声明。跟我最开始的写法一样，不过比我写的好地方在于把这个从mid往前查找的动作放在了二分的循环里面。

	   int left = 0;
       int right = values.length - 1;
       int mid = left + ((right - left) >> 1);
       while (left < right) {
           if (values[mid] < target) {
               left = mid + 1;
           } else if (values[mid] > target) {
               right = mid - 1;
           } else {
               if (mid == 0 || (values[mid-1] != target))
                   return mid;
               else
                   right = mid - 1;
           }
           mid = left + ((right - left) >> 1);
       }
       
       return -1;

查找最后一个值等于给定值的元素是类似的，明白等于的情况交给谁处理会出现什么样的结果，那就很好办了，找最后一个值就是把等于的情况交给左边界来处理，往右压缩，最后一个值等于给定值的元素会被压缩到右边界。

public static int lastEqual(int[] values, int target) {
        int left = 0;
        int right = values.length - 1;
        int mid = left + ((right - left) >> 1);
        while (left < right) {
            if (values[mid] <= target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
            mid = left + ((right - left) >> 1);
        }
        if (right < values.length && values[right] == target)
            return right;
        return -1;
    }

对应的，这样更好理解呢~

        int left = 0;
        int right = values.length - 1;
        int mid = left + ((right - left) >> 1);
        while (left < right) {
            if (values[mid] < target) {
                left = mid + 1;
            } else if (values[mid] > target) {
                right = mid - 1;
            } else {
                if (mid == 0 || values[mid + 1] != target)
                    return mid;
                else
                    left = mid + 1;
            }
            mid = left + ((right - left) >> 1);
        }

        return -1;

2.2、查找第一个大于等于、最后一个小于等于给定值的元素

找第一个大于等于给定值 = 找一个最小右边界。
找最后一个小于等于给定值 = 找一个最大左边界。

public static int lastMin(int[] values, int target) {
        int left = 0;
        int right = values.length - 1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (values[mid] <= target) {
                if (mid == values.length-1 || values[mid + 1] > target)
                    return mid;
                else
                    left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return -1;
    }
    public static int firstMax(int[] values, int target) {
        int left = 0;
        int right = values.length - 1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (values[mid] >= target) {
                if (mid == 0 || values[mid - 1] < target)
                    return mid;
                else
                    right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }

2.3、思考题

在一个循环有序数组中查找值等于给定值的情况，如在[4,5,6,1,2,3]中查找2。

public static int findTargetInCircle(int[] values, int target) {
        int length = values.length;
        int left = 0;
        int right = length - 1;
        int mid = -1;
        while (left <= right) {
            mid = left + ((right - left) >> 1);
            if (values[mid] == target) {
                return mid;
            } else if (values[mid] > target) {
                if (values[mid] >= values[left] && values[left] > target) {
                    left = mid + 1;
                } else {
                    right = mid - 1;
                }
            } else {
                if (values[mid] <= values[right] && values[right] < target) {
                    right = mid - 1;
                } else {
                    left = mid + 1;
                }
            }
        }

        return -1;
    }

炫耀，leetcode上的第33题。

同理，对循环的数组求上面四个二分的变形问题，只需要把values[mid] == target时的处理加到对应的位置即可~