原型聚类之K均值算法及Python实现

原型聚类(prototype-based clustering)

原型聚类，此类算法假设聚类结构能通过一组原型刻画，在现实聚类任务中极为常用，通常情形下，算法先对原型进行初始化，然后对原型进行迭代更新求解，采用不同的原型表示，不同的求解方式，将产生不同的算法，主要有：K均值算法、学习向量量化和高斯混合聚类。

K均值算法

K均值算法，顾名思义，可知将一组数据 D={x1,x2,...,xm} D = { x 1 , x 2 , . . . , x m } 聚成K类,”均值”是指对聚类所得簇划分 C={C1,C2,...,Ck} C = { C 1 , C 2 , . . . , C k } 最小化平方误差

E=∑i=1k∑x∈Ci∥x−μi∥22(1.1) (1.1) E = ∑ i = 1 k ∑ x ∈ C i ‖ x − μ i ‖ 2 2

其中 μi=1|Ci|∑x∈Ci μ i = 1 | C i | ∑ x ∈ C i 是簇 Ci C i 的均值向量，直观上看，式(1.1)在一定程度上刻画了簇内样本围绕均值向量的紧密程度，E值越小则簇内样本相似度越高；话不多说，直接将算法(贪心策略)书写如下（参考周志华的《机器学习》）：

---

输入：样本集 D={x1,x2,...,xm}； D = { x 1 , x 2 , . . . , x m } ；
   聚类簇数 k k
过程：
1. 从 D D 中随机选择k个样本作为k均值向量 {μ1,μ2,...,μk} { μ 1 , μ 2 , . . . , μ k }
2. repeat
3.  令 Ci=∅(1≤i≤k) C i = ∅ ( 1 ≤ i ≤ k )
4.  for j=1,2,...,m j = 1 , 2 , . . . , m do
5.  计算样本 xj x j 与各均值 μi μ i 的距离： dji=∥xj−μi∥2 d j i = ‖ x j − μ i ‖ 2 ;根据距离最近的均值向量确定 xj x j 的簇标记： λj=argmini∈{1,2,...,k}dji λ j = a r g m i n i ∈ { 1 , 2 , . . . , k } d j i 将样本 xj x j 划入相应的簇： Cλj=Cλj⋃{xj} C λ j = C λ j ⋃ { x j }
5.  end for
6.  for i=1,2,..,k i = 1 , 2 , . . , k do
7.   计算新均值向量： μi′=1|Ci|∑x∈Ci μ i ′ = 1 | C i | ∑ x ∈ C i
8.   if μi′≠μi μ i ′ ≠ μ i then
9.    将当前均值向量 μi μ i 更新为 μi′ μ i ′
10.   else
11.    保持当前均值不变
12.   end if
13.  end for
14. until 当前均值向量均未更新
输出：簇划分 C={C1,C2,...,Ck} C = { C 1 , C 2 , . . . , C k }

python手写k-means算法

# 计算距离 这是使用的L2
def distEclud(vecA, vecB):
    return np.sqrt(np.sum(np.power(vecA - vecB, 2)))  # la.norm(vecA-vecB)

# 随机生成中心均值点
def randCent(dataSet, k):
    n = np.shape(dataSet)[1]
    centroids = np.mat(np.zeros((k, n)))  # create centroid mat
    for j in range(n):  # create random cluster centers, within bounds of each dimension
        minJ = min(dataSet[:, j])
        rangeJ = float(max(dataSet[:, j]) - minJ)
        centroids[:, j] = np.mat(minJ + rangeJ * np.random.rand(k, 1))
return centroids

# kMeans算法
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
   m = np.shape(dataSet)[0]
   clusterAssment = np.mat(np.zeros((m, 2)))  # 用于分配数据点
   centroids = createCent(dataSet, k)  # 随机生成k个均值向量
   clusterChanged = True
   while clusterChanged:
       clusterChanged = False
       for i in range(m):  #为每个数据点分配到最近的均值向量上
           minDist = np.inf
           minIndex = -1
           for j in range(k):
               distJI = distMeas(centroids[j, :], dataSet[i, :])
               if distJI < minDist:  
                   minDist = distJI  
                   minIndex = j
           if clusterAssment[i, 0] != minIndex:
               clusterChanged = True
           clusterAssment[i, :] = int(minIndex), minDist ** 2
       for cent in range(k):  # recalculate centroids
           ptsInClust = dataSet[np.nonzero(clusterAssment[:, 0].A == cent)[0]]  # get all the point in this cluster
           centroids[cent, :] = np.mean(ptsInClust, axis=0)  # assign centroid to mean
return centroids, clusterAssment

K-means的python实例(使用scipy.cluster)

数据来源是Old Faithful Geyser，有些时候我们可能不知道最终究竟聚成多少类，一个办法是先对数据进行用层次聚类(后面的文章将会介绍)，通过观察层次聚类后的树状图对K值进行初始化，当然也可以直接输入某个数值。由于K-means算法有现成的实现，scipy.cluster是scipy下的一个做聚类的package，所以我们没有必要自己实现，直接使用上面的模块即可。
在给出完整代码之前，我先介绍一下几个代码中使用到的函数，以方便理解。
1.linkage(y, method=’single’, metric=’euclidean’)
共包含3个参数:
y是距离矩阵,由pdist得到;method是指计算类间距离的方法,比较常用的有3种:
(1)single:最近邻,把类与类间距离最近的作为类间距
(2)complete:最远邻,把类与类间距离最远的作为类间距
(3)average:平均距离,类与类间所有pairs距离的平均
其他的method还有如weighted,centroid等等,具体可以参考
http://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.hierarchy.linkage.html#scipy.cluster.hierarchy.linkage
2.fcluster(Z, t, criterion=’inconsistent’, depth=2, R=None, monocrit=None)
第一个参数Z是linkage得到的矩阵,记录了层次聚类的层次信息; t是一个聚类的阈值-“The threshold to apply when forming flat clusters”,在实际中,感觉这个阈值的选取还是蛮重要的.
其他的参数我用的是默认的,具体可以参考:
http://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.hierarchy.fcluster.html#scipy.cluster.hierarchy.fcluster
3.kmeans(obs, k_or_guess, iter=20, thresh=1e-05, check_finite=True)
输入obs是数据矩阵,行代表数据数目,列代表特征维度; k_or_guess表示聚类数目;iter表示循环次数,最终返回损失最小的那一次的聚类中心;
输出有两个,第一个是聚类中心(codebook),第二个是损失distortion,即聚类后各数据点到其聚类中心的距离的加和.
可参考http://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.vq.kmeans.html#scipy.cluster.vq.kmeans
4.vq(obs, code_book, check_finite=True)
根据聚类中心将所有数据进行分类.obs为数据,code_book则是kmeans产生的聚类中心.
输出同样有两个:第一个是各个数据属于哪一类的label,第二个和kmeans的第二个输出是一样的,都是distortion
可参考http://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.vq.vq.html#scipy.cluster.vq.vq
实例代码如下：
可以从github下载。

###cluster.py
#导入相应的包
import scipy
import scipy.cluster.hierarchy as sch
from scipy.cluster.vq import vq,kmeans
import numpy as np
import matplotlib.pylab as plt
#归一化的Old Faithful Geyser:scaledfaithful.txt
data = np.loadtxt('scaledfaithful.txt')

#1. 层次聚类
#生成点与点之间的距离矩阵,这里用的欧氏距离:
disMat = sch.distance.pdist(data,'euclidean')
#进行层次聚类:
Z=sch.linkage(disMat,method='average')
#将层级聚类结果以树状图表示出来并保存为plot_dendrogram.png
plt.figure(num=1)
P=sch.dendrogram(Z)
plt.savefig('plot_dendrogram.png')
#根据linkage matrix Z得到聚类结果:
cluster= sch.fcluster(Z, t=1, criterion='inconsistent')
print(max(cluster))
#print("Original cluster by hierarchy clustering:\n",cluster)


#2. k-means聚类
#使用kmeans函数进行聚类,输入第一维为数据,第二维为聚类个数k.
#有些时候我们可能不知道最终究竟聚成多少类,一个办法是用层次聚类的结果进行初始化.当然也可以直接输入某个数值.
#k-means最后输出的结果其实是两维的,第一维是聚类中心,第二维是损失distortion,我们在这里只取第一维,所以最后有个[0]
centroid=kmeans(data,5)[0]

#使用vq函数根据聚类中心对所有数据进行分类,vq的输出也是两维的,[0]表示的是所有数据的label
label=vq(data,centroid)[0]
color = ("red", "green","yellow","black","blue")
print ("Final clustering by k-means:\n",label)
colors=np.array(color)[label]
plt.figure(num=2)
plt.scatter(data[:, 0], data[:, 1], c=colors)
plt.show()

最后来看看聚类的效果，如下图所示
层次聚类结果的树状图：

通过观察上面的树状图，我们可以将数据分为4类，聚类结果如下：

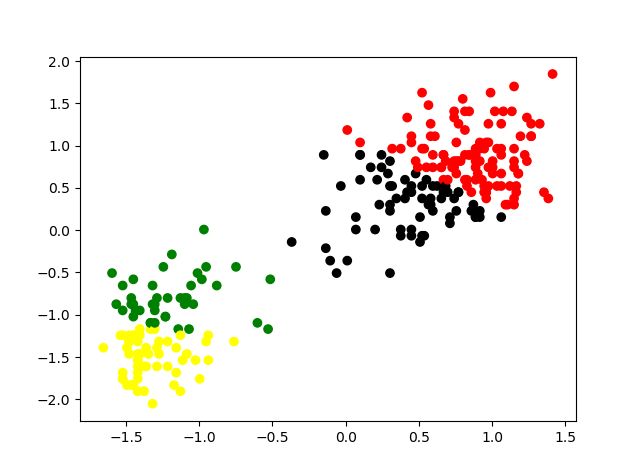
k-means算法优缺点

优点：k-means是一个简单并且很有效的聚类方法，算法收敛很快，相对高效和高扩展性。算法复杂度为 O(t⋅k⋅n) O ( t ⋅ k ⋅ n ) ，其中 t t 为迭代次数 k k 为中心点个数 n n 为样本个数。
缺点: 需要先验和主观知识指定聚类中心个数 k k ，对噪点比较敏感，可能会陷入局部最优(实际过程中，可以选择多个不同初始化点)。

---

更多机器学习干货、最新论文解读、AI资讯热点等欢迎关注”AI学院(FAICULTY)”
欢迎加入faiculty机器学习交流qq群：451429116 点此进群
版权声明：可以任意转载，转载时请务必标明文章原始出处和作者信息.

---

参考文献

[1]. 周志华，机器学习，清华大学出版社，2016
[2]. 使用scipy进行层次聚类和k-means聚类
[3]. 机器学习Chapter3-(聚类分析)Python实现K-Means算法