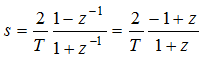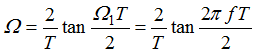数字信号处理--语音信号处理

摘 要

语音信号处理是研究用数字信号处理技术对语音信号进行处理的一门学科。语音信号处理的目的是得到某些参数以便高效传输或存储，或者是用于某种应用。本设计利用计算机Windows下的录音机录入一句语音信号，在Matlab平台上对其进行时域分析和频域分析，并对所采集的语音信号加入干扰噪声，对加噪语音信号进行时域和频域分析，以确定加噪信号的频率分布情况，从而确定滤波器的相关参数。进一步用双线性变换法设计切比雪夫Ⅱ型的滤波器，然后对加噪的语音信号进行滤波处理。比较滤波前后的语音信号的时域和频域特性，回放加噪语音信号和去噪语音信号，从而分析滤波性能。

 

关键词：

Matlab，语音信号，时域分析，频域分析，滤波器

 

语音信号处理系统设计

一、课程设计的目的

1、学会MATLAB的使用，掌握基本MATLAB程序设计方法；

2、掌握数字信号处理的一些基本概念、基本理论和基本方法；

3、掌握在Windows环境下采集语言信号的方法；

4、掌握MATLAB设计IIR数字滤波器的方法；

5、掌握用MATLAB对信号进行分析和处理的方法；

二、设计要求及任务

1. 语音信号的采集

本设计利用计算机Windows下的录音机录入一句语音信号，然后在Matlab软件平台下，利用函数waveread对语音信号进行采样，记住采样频率和采样点数。

1. 语音信号的频谱分析

在Matlab中，可以利用函数FFT对信号进行快速傅里叶变换，得到信号的频谱特性，然后加入一干扰信号，要求画出语音信号干扰前后的时域波形，并对其频谱进行分析。

1. 设计数字滤波器，给出性能指标（参考指标）

（1）低通滤波器的性能指标：f_p=1000Hz,f_s=1200Hz,A_s=100dB, A_p=1dB

（2）高通滤波器的性能指标：f_s=4800Hz,f_p=5000Hz,A_s=100dB, A_p=1dB

（3）带通滤波器的性能指标：f_p1=1200Hz,f_p2=3000Hz,f_s1=1000Hz,

f_ps2=3200Hz,A_s=100dB,A_p=1dB；

采用双线性变换法设计上面一种类型的数字滤波器，要求使用切比雪夫II型滤波器。

1. 用滤波器对信号进行滤波

画出滤波后信号的时域波形及频谱，并对滤波前后的信号进行对比，分析信号的变化。

1. 回放语音信号，分析滤波前后的语音变化

在熟悉数字信号处理课程理论的基础上，通过MATLAB仿真实现语音信号的采集与处理，进一步加深对数字信号处理理论和技术的掌握。

三、课程设计平台

计算机、MATLAB6.5以上。

四、计原理与计算方法

1. 卷积运算

卷积和乘积运算在频域和时域是一一对应的，两个信号在时域的卷积可以转化为求两者在频域的乘积后再反变换，同理在频域的卷积等时域的乘积。而信号的频域求解有快速傅里叶FFT算法。

卷积与傅里叶变换有着密切的关系。利用这一点性质，即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换，能使傅里叶分析中许多问题的处理得到简化。

由卷积得到的函数f*g 一般要比f 和g 都光滑。特别当g 为具有紧支集的光滑函数，f 为局部可积时，它们的卷积f * g 也是光滑函数。利用这一性质，对于任意的可积函数f，都可以简单地构造出一列逼近于f 的光滑函数列，这种方法称为函数的光滑化或正则化。

卷积的概念还可以推广到数列、测度以及广义函数上去。

1. 采样定理

采样定理，又称香农采样定理，奈奎斯特采样定理，是信息论，特别是通讯与信号处理学科中的一个重要基本结论。E.T.Whittaker(1915年发表的统计理论),克劳德·香农与Harry Nyquist都对它作出了重要贡献。另外，V.A.Kotelnikov也对这个定理做了重要贡献。

　 采样是将一个信号（即时间或空间上的连续函数）转换成一个数值序列（即时间或空间上的离散函数）。采样定理指出，如果信号是带限的，并且采样频率高于信号带宽的两倍，那么，原来的连续信号可以从采样样本中完全重建出来。

带限信号变换的快慢受到它的最高频率分量的限制，也就是说它的离散时刻采样表现信号细节的能力是有限的。采样定理是指，如果信号带宽不到采样频率的一半（即奈奎斯特频率），那么此时这些离散的采样点能够完全表示原信号。高于或处于奈奎斯特频率的频率分量会导致混叠现象。大多数应用都要求避免混叠，混叠问题的严重程度与这些混叠频率分量的相对强度有关。

1. 双线性变换法设计IIR低通数字滤波器的基本原理

双线性变换法设计数字滤波器，采用了二次映射的方法，就是先将整个s平面压缩到s₁平面的一个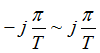的横形条带范围内，然后再将这个条带映射到z平面上，就能建立s平面到z平面的一一对应关系。对于低通数字滤波器，映射关系为

(1)

其中T为抽样周期。

用双线性变换法设计低通IIR数字滤波器的基本步骤，首先根据设计要求确定相应的模拟滤波器的传递函数，再应用(1)式得数字滤波器的传递函数

　　　　　　　　 (2)

通常可以给定的参数为：低通数字滤波器通带边界频率、阻带边界频率和对应的通带衰减函数、阻带衰减函数。s₁平面中的模拟角频率与数字角频率的关系为线性关系，在计算模拟滤波器的阶数N、极点s_i和传递函数之前，应作预畸变处理

　　 (3)

模拟滤波器的阶数N、极点s_i和传递函数的计算方法与冲激响应不变法相同，可以采用Butterworth逼近或Chebyshev逼近。

Chebyshev 滤波器则比Butterworth 滤波器的截止特性要好，在期望通带下降斜率大的场合，应使用椭圆滤波器或切比雪夫滤波器。在MATLAB下可使用cheby2函数设计出切比雪夫II型IIR滤波器。但阻带处的幅值有振荡。对于数字滤波器而言，可以采用不同阶数逼近相应滤波器，滤波器性能还与滤波器的阶数有关，一般而言，阶数越高，则逼近越精确，但计算代价也随之上升，所以性能与代价总需要寻求一个平衡点。本设计用Chebyshev 滤波器。

1. 双线性变换法设计IIR高通、带通、带阻数字滤波器的基本原理

由于双线性变换法获得的数字滤波器频率响应特性中不会出现混叠现象，因此可以适用于高通、带通和带阻滤波器的设计。IIR数字滤波器的设计通常要借助于模拟低通滤波器的设计，由原型低通滤波器到其他形式（高通、带通、带阻）IIR数字滤波器的频带变换有模拟频带变换法和数字频带变换法。

（1）模拟频带变换法

首先将给定的对数字滤波器(DF)的技术要求转换为一个低通模拟滤波器(AF)的技术要求，根据这种要求用某种逼近设计出原型的低通模拟滤波器(LP AF)，计算出模拟滤波器的阶数N、极点s_i和传递函数，再按照双线性变换的变换关系，将模拟滤波器的传递函数转换为数字滤波器的传递函数。

（2）数字频带变换法

首先将给定的对数字滤波器(DF)的技术要求转换为一个低通模拟滤波器(AF)的技术要求，用双线性变换法将原型的低通模拟滤波器(LP AF)映射为低通数字滤波器，再将数字低通滤波器根据相应的变换公式经频带变换到各型数字滤波器。

（3）IIR数字滤波器的设计

可利用MATLAB提供的函数直接设计相应的数字滤波器。

五、实验论证方案

本次课程设计是要对生活中常见的语音信号进行分析处理。信号分析处理要经过语音信号的采集、时域和频域波形的分析，设计干扰信号，原始信号和干扰信号的融合，IIR滤波器的设计，滤波等几个步骤。

1. 语音信号的录入与打开

方案一：在Matlab中，waveread函数用于录入语音，语音必须是.wav格式。

方案二：在高版本的Matlab中，也可以使用audioread函数来替换waveread函数，语音格式可以是.mp3格式。

本次设计中我们使用的是Matlab 2010版，所以使用方案一进行语音信号的采集。

语音打开所用的函数为sound(y,fs,bits)，用于对声音的回放，向量y表示语音信号，fs表示采样频率，bits表示采样位数。

1. 语音信号的频域分析

本次课程设计主要对语音信号进行快速傅里叶变换（FFT）来分析其频域特性。

Matlab的信号处理工具箱中的函数FFT可用于对序列的快速傅里叶变换分析，其调用格式是y=fft(x,N)，其中，x是序列，y是序列的FFT变换结果，N为整数，代表做N点的FFT，若x为向量且长度小于N，则函数将x补零至长度N；若向量x长度大于N，则截断x使之长度为N。

一般FFT程序中所用数据点数与原含有信号数据点数相同，这样的频谱图具有较高的质量，可减小因补零或截断而产生的影响。

1. 干扰噪声的设计

噪声可以是随机产生的白噪声或者是正余弦噪声。通过分析可以得到原始语音信号的频率范围，为便于后续滤波器的设计我们设计的滤波器频率为11000。幅度选择0.017V，幅度大小合适。

方案一：正弦和余弦噪声的频谱是规则的两条竖线，频率和幅度可根据自己设定的参数进行调整，信号容易产生切杂波容易滤去。

方案二：Matlab中，随机产生的噪声用y=rand(a,b)实现，其噪声频谱是不规则的，且滤除时较困难。

为方便后续滤波器的设计，我们采用方案一的干扰噪声设计方法。

1. 数字滤波器的设计
2. 模拟滤波器原理

方案一：采用巴特沃斯滤波器。巴特沃斯滤波器的频率特性曲线，无论在通带内还是阻带内都是频率的单调函数。因此，当通带的边界处满足指标要求时，通带内肯定会有裕量。巴特沃斯滤波器通带、阻带均无波动，结构简单，阻带衰减速度较慢。同等条件下巴特沃斯滤波器的阶数最高。

方案二：采用切比雪夫滤波器。切比雪夫滤波器的幅频特性具有等波纹特性。有两种形式:在通带内等波纹、在阻带内单调的是切比雪夫I型滤波器，在通带内单调、在阻带内等波纹的是切比雪夫II滤波器。切比雪夫滤波器通带有波动，边带仍为单调上升函数，结构复杂，边带截止率可以做的较陡峭。切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小。

本次设计我们选择阶数小，阻带等波纹的切比雪夫Ⅱ型的数字滤波器。

1. 模拟滤波器数字化原理

模拟滤波器转化为数字滤波器在工程上常用的有冲激响应不变法和双线性变换法。

方案一：冲激响应不变法是一种时域上的转换方法，它是数字滤波器的单位取样响应在抽样点上等于模拟滤波器的单位冲激响应，这种方法s和z的关系是:。该方法的优点是频率坐标变换时线性的数字滤波器的单位脉冲响应完全模仿模拟滤波器的单位冲激响应，时域特性逼近好；缺点是会产生频谱混叠现象，适合低通、带通滤波器的设计，不适合高通、带阻滤波器的设计。

方案二：双线性变换法为了克服频谱混叠现象，采用非线性频率压缩方法，将整个频率轴上的频率范围压缩到π/T之间，再用转换到Z平面上。双线性变换法中，s和z的关系是：。该方法克服了频谱混叠现象，但带来了频率坐标变换的非线性：。

本次设计中需要分析频谱特性，为避免产生频谱混叠现象而且需要设计带阻滤波器，因而我们采用了方案二。

1. 滤波器参数设计方案

按照之前的原始语音信号频谱图和所加入的噪声频率，对滤波器进行设计以及参数的确定。包括通带截止频率wp、阻带截至频率ws、通带最小衰减增益Ap，阻带最大衰减增益As。

本次设计的低通、带通、带阻三种滤波器加以分析: 其中带通滤波器是由高通滤波器和低通滤波器组成，带阻滤波器是由低通滤波器和高通滤波器组成，我们的原始语音信号主要集中在低频，所以三种滤波器都可以有效的滤除噪声。

六、实验结果及分析

利用MATLAB软件对语音信号进行频谱分析、对加入噪声的信号进行频谱分析、设计合适的滤波器滤除噪声。

1. 语音信号的录入和分析
2. 音频信号采样

用电脑所带的录音工具录制一段录音，使用waveread函数读取语音信号的数据，用sound函数播放语音。

程序如下：

%音频信号采样

[y1,fs,bit] = wavread('zhou.wav');

figure(1);

subplot(2,1,1);plot( y1 );

title( '原语音信号时域波形图' );

xlabel( '单位/t' );ylabel( '幅度' );

1. 频谱特性分析：

   利用MATLAB对语音信号进行FFT分析，并画出原语音信号的时域波形图和频谱特性图。

   %采样后进行fft得到频域

   N= length(y1);

   f1= (0:N-1)*fs/N;

   y2 = fft (y1,N);

   subplot(2,1,2);plot( f1, abs(y2) );

axis([-10000 20000 0 15000]);

title( '原语音信号频域波形图' );

xlabel('单位/hz');ylabel('幅度');

1. 运行结果如下：

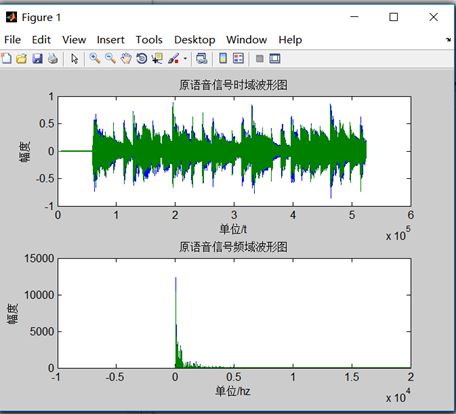
图1-1原始语音信号频谱图及FFT频谱图

1. 结果分析如下：

从图1-1可以看出，原始语音信号的频率基本上集中在5kHz以内。其中原始语音信号FFT频谱和原始语音信号频谱的区别是：前者是频率为1递增的频谱，而后者是以f1= (0:N-1)*fs/N递增，后者是在"不小于原始信号的频率（采样定理）"上完全展开的频谱。

1. 加入噪声信号
2. 干扰信号设计：

选取余弦函数产生一个噪声信号，其频率为1.1kHz。对加噪后的语音信号进行播放。

程序如下：

%所加的干扰信号

t=0:1/fs:(N-1)/fs;

y3=0.17*cos(2*pi*11000*t);

figure(2); subplot(2,1,1);plot(y3);

title( '干扰信号时域波形图' );

xlabel( '单位/t' ); ylabel( '幅度' );

 

1. 干扰信号和原始信号的融合

程序如下：

%加噪后的语音信号

y1=y1(:,1); %将有y12维向量转化成1维向量

y3=y3'; %y1是行向量，y3是列向量，需转置

y5=y1+y3;

figure(3);subplot(2,1,1);plot(y5);

title( '加噪之后信号时域图' );

xlabel('单位/t');ylabel('幅度');

1. 加噪后信号频域分析

对其做FFT，进行时域和频域的分析，比较加噪前后语音信号的波形及频谱。

程序如下：

y6= fft (y5);

subplot(2,1,2);plot( f1, abs(y6) );

axis([-10000 20000 0 50000 ]);

title( '加噪之后信号频谱图' );

xlabel('单位/hz');ylabel('幅度');

1. 运行结果如下：

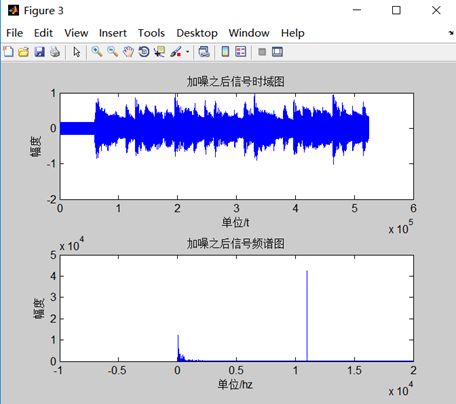
图2-1 加噪后的信号时域波形图

1. 结果分析：

在加入频率为1.1kHz的余弦噪声后，绘制其时域波形图和频谱图，比较图1-1和图2-1可发现，频谱图可以直观的看出所加噪声的频率和谱线。在播放音频时可以明显听到有刺耳的噪声。

 

1. 滤波器的设计

用双线性变换法设计了切比雪夫Ⅱ型低通、带阻、带通IIR滤波器，并分别绘制滤波器的幅频图。

1. 切比雪夫Ⅱ型低通滤波器：

设计低通滤波器时所取通带截止频率取fp=4kHz，阻带截止频率取fs=8kHz，通带最大衰减波纹Rp=1，阻带最小衰减As=80。确定参数后用双线性变换法转换为数字低通滤波器 。

程序如下：

% 低通滤波器设计

wp=2*pi*4000/fs;ws=2*pi*8000/fs;

omegap=2*fs*tan(wp/2);

omegas=2*fs*tan(ws/2);

rp=1;as=80;

[N,omegaC]=cheb2ord(omegap,omegas,rp,as,'s');

[b,a]=cheby2(N,as,omegas,'s');

[bz,az]=bilinear(b,a,fs);

[h,w]=freqz(bz,az);

w0=[omegap,omegas];

hx=freqz(bz,az,w0);

dbhx=-20*log10(abs(hx));

figure(4);

subplot(2,1,1);plot(w/(2*pi)*fs,20*log10(abs(h)));

title('切比雪夫ii型低通滤波器幅频响应');

y7=filter(bz,az,y5);

figure(5);subplot(2,1,1);plot(y7);

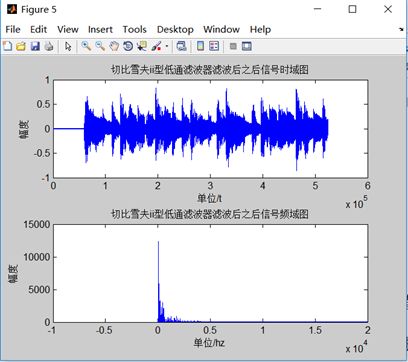
title( '切比雪夫ii型低通滤波器滤波后之后信号时域图' );

xlabel('单位/t'); ylabel('幅度');

y8 = fft (y7);

subplot(2,1,2);plot(f1,abs(y8));

axis([-10000 20000 0 15000 ]);

title( '切比雪夫ii型低通滤波器滤波后之后信号频域图' );

图3-1 低通滤波器

图3-2 低通滤波器滤波后语音信号的频谱图

1. 切比雪夫Ⅱ型带阻滤波器：

设计带阻滤波器时通带上截止频率取fp1=3kHz，通带下截止频率取fp2=20kHz阻带下截止频率取fs1=6kHz，阻带上截止频率取fs2=1.5kHz，，通带最大衰减波纹Rp=1，阻带最小衰减As=100。确定参数后做频率预畸变化，用双线性变换法转换为数字带阻滤波器。

程序如下：

%带阻滤波器

wp1=2*pi*3000/fs;wp2=2*pi*20000/fs;

ws1=2*pi*6000/fs;ws2=2*pi*15000/fs;

Rp=1;As=100;

T=1/fs;

omegap1=(2/T)*tan(wp1/2);

omegap2=(2/T)*tan(wp2/2);

omegap=[omegap1,omegap2];

omegas1=(2/T)*tan(ws1/2);

omegas2=(2/T)*tan(ws2/2);

omegas=[omegas1,omegas2];

[N,omegac]=cheb2ord(omegap,omegas,Rp,As,'s');

[b,a]=cheby2(N,As,omegas,'stop','s');

[bz,az]=bilinear(b,a,fs);

[H,w]=freqz(bz,az);

w0=[omegap,omegas];

hx=freqz(bz,az,w0);

dbhx2=-20*log10(abs(hx));

figure(8);

subplot(2,1,1);plot(w/(2*pi)*fs,20*log10(abs(H)));

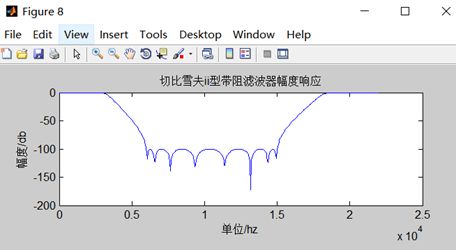
title('切比雪夫ii型带阻滤波器幅度响应');

xlabel('单位/hz');ylabel('幅度/db');

y11=filter(bz,az,y5);

figure(9);subplot(2,1,1);plot(y11);

title( '切比雪夫ii型带阻滤波器滤波后之后信号时域图' );

xlabel('单位/t');ylabel('幅度');

y12 = fft (y11);

subplot(2,1,2);plot(f1,abs(y12));

axis([-10000 20000 0 15000 ]);

title( '切比雪夫ii型带阻滤波器滤波后之后信号频域图' );

xlabel('单位/t');ylabel('幅度');

程序运行结果如下：

图3-3 带阻滤波器

图3-4 带阻滤波器滤波后语音信号的频谱图

1. 切比雪夫Ⅱ型带通滤波器：

设计带通滤波器时通带上截止频率取fp1=100Hz，通带下截止频率取fp2=4kHz，上阻带截止频率取fs1=10Hz，下阻带截止频率取fs2=10kHz，通带最大衰减波纹Rp=1，阻带最小衰减As=60。确定参数后做频率预畸变化，用双线性变换法转换为数字带通滤波器。

程序如下：

%带通滤波器

wp1=2*pi*100/fs;wp2=2*pi*4000/fs;

ws1=2*pi*10/fs;ws2=2*pi*10000/fs;

Rp=1;As=60;

T=1/fs;

omegap1=(2/T)*tan(wp1/2);

omegap2=(2/T)*tan(wp2/2);

omegap=[omegap1,omegap2];

omegas1=(2/T)*tan(ws1/2);

omegas2=(2/T)*tan(ws2/2);

omegas=[omegas1,omegas2];

[N,omegac]=cheb2ord(omegap,omegas,Rp,As,'s');

[b,a]=cheby2(N,As,omegas,'s');

[bz,az]=bilinear(b,a,fs);

[H,w]=freqz(bz,az);

w0=[omegap,omegas];

hx=freqz(bz,az,w0);

dbhx1=-20*log10(abs(hx));

figure(4);subplot(2,1,2);plot(w/(2*pi)*fs,20*log10(abs(H)));

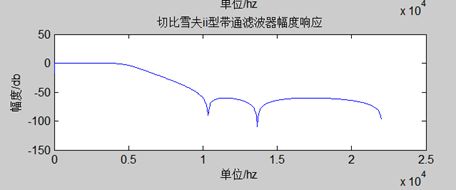
title('切比雪夫ii型带通滤波器幅度响应');

xlabel('单位/hz');ylabel('幅度/db');

y9=filter(bz,az,y5);

figure(7);subplot(2,1,1);plot(y9);

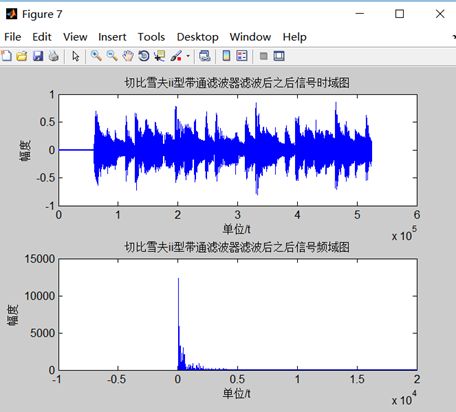
title( '切比雪夫ii型带通滤波器滤波后之后信号时域图' );

xlabel('单位/t');ylabel('幅度');

y10 = fft (y9);

subplot(2,1,2);plot(f1,abs(y10));

axis([-10000 20000 0 15000 ]);

title( '切比雪夫ii型带通滤波器滤波后之后信号频域图' );

xlabel('单位/t');ylabel('幅度');

程序运行结果如下：

图3-5 带通滤波器

图3-6 带通滤波器滤波后语音信号频谱图

1. 结果对比分析：

在切比雪夫Ⅱ型下设计的低通、带通、带阻三种滤波器中，分别将图3-2、3-4、3-6与图1-2比较后发现，三种滤波器都可以有效的达到滤波效果。其中滤波效果比较好的是带阻滤波器和低通滤波器，对原始语音影响最小，而带通滤波器效果是三种中最差的，因为带通滤波器的下阻带截止频率和通带下截止频率的取值会对原语音信号造成影响，使信号失真较多。

本次设计中Rp、As的取值是经过调试后能够使滤波器性能达到最优的值，通过调试可以得知，在设计滤波器中，阶数N越大，滤波器结构越复杂，精度越高，滤波效果越好。

七、课程设计中遇到的问题及解决方法

1. 问题：对原始信号作频谱分析时，画出的频谱图关于横轴对称，且成镜像分布。

由于使用plot函数画图时没有使用abs(y)来取绝对值，所以频谱的幅值有正有负；而且没有设置横纵坐标轴的范围，所以横轴值过大，频谱成镜像分布。通过查阅plot函数使用格式，修改程序plot(f,abs(y))，添加坐标轴设置函数axis([x1 x2 y1 y2]);grid，解决问题。

1. 问题：添加噪声时添加不上，且运行时有错误提示噪声不能直接与语音信号相加。

在Matlab中运行程序时，提示噪声与原语音不能直接使用"+"相加，上网查阅资料之后明白我们所录制的语音是二维的，而噪声是一维的，需要通过取原始语音信号的单声道信号和噪声信号相加，于是添加如下程序：

y1=y1(:,1);

y3=y3';

y5=y1+y3;

1. 问题：在设置的余弦噪声中，频率与频谱图不相符，不清楚噪声的频率与频谱图是什么关系。

在频谱图中，按照理论噪声的频谱图应该与设置的频率相符，但我们最开始时设置的噪声频率与所画出的频谱图有较大差距，修改程序：f1= (0:N-1)*fs/N; 后所设置的频率即为频谱图上所显示的频率。

1. 问题：设计带通滤波器时，下阻带截止频率和通带下截止频率始终会对原始信号造成影响。

调试参数时Rp、As与带阻和低通都有较大差距。将加噪后的语音信号经过带通滤波器，使滤波器滤除原始信号，留下噪声信号，再用加噪信号减去噪声信号可得到原始语音，多次调整fp1和fs1使其到最佳数值，尽量减少对原始噪声的影响。

八、课程设计总结

通过这次课设，使我对滤波器有了更深的认识，特别是滤波器参数对滤波器性能的影响，因为通带截止频率、阻带截止频率、通带衰减、阻带衰减都要影响滤波器的阶数，而滤波器的阶数越大，其选频特性就越好。并且不同的滤波器类型可达到的滤波效果也不同，要根据衰减系数选择合适的滤波器。

在做这次课设的过程中，也遇到了些困难，尤其是GUI界面的设计。由于起初对GUI界面设计不了解，花费了些时间在学习使用方面，例如希望可以在界面中播放滤波前后的信号，才知道不同的function是独立执行的，如果想在一个function中使用其他function中变量的值，则需要用save和load来分别保存和调用变量。

这次课设使我认识到matlab软件功能的强大，可以完成各类信号处理相关的功能，我的这个课题只是小小的一部分，今后我还需更加努力完善自己，用会，用精matlab来分析解决问题，将理论联系实际，获得更大提高。

这期间遇到了很多困难和问题，但是通过自己的探索也学到了很多东西，不仅重新复习了书本上滤波器部分的原理，对其有了新的理解，而且又学到了很多书上没有的知识。通过程序编写过程中产生的各种各样的错误提示，亲自动手去查资料才知道错误所在，也正是这个探索的过程让我有了更大的进步。但设计中还存在很多不足的地方，比如设计的滤波器方法和类型比较单一，没有做更多的滤波效果比较。

通过这次课程设计，我深刻体会到应用Matlab进行语音信号处理与我们所学课程及专业的紧密关联，也让我体会到理论与实际的结合的重要性和两者之间的差别，也学到了课堂上学不到的东西。

九、参考文献

[1] 高西全、丁玉美编著，数字信号处理。西安：西安电子科技大学出版社，2008.

[2]丁玉美、高西全编著，数字信号处理学习指导。西安：西安电子科技大学出版社，2001.

[3]郑君里等编，信号与系统。北京：高等教育出版社，2000.

[4]刘树棠译，数字信号处理——使用MATLAB。西安：西安交通大学出版社，2002.

[5]导向科技编著，MATLAB程序设计与实例应用。北京：中国铁道出版社，2001.

[6]罗军辉等编著，MATLAB7.0在数字信号处理中的应用。北京：机械工程出版社，2005.

[7]陈怀琛等编著，MATLAB及在电子信息课中的应用。北京：电子工业出版社，2002.

[8]胡广书编组，数字信号处理——理论、算法与实现。北京：清华大学出版社，2002.

[9]梁虹等编，信号与线性系统分析——机遇MATLAB的方法与实现。北京：高等教育出版社，2006.

[10]刘卫国主编，MATLAB程序设计与应用（第二版）。北京：高等教育出版社，2006.