论文(3) Focal Loss
Focal Loss
@(目标检测)
Focal Loss是KaiMing大神提出来的,这篇文章的重点在于分析了one-stage网络的检测精度为什么会弱于two-stage的网络。当原理分析出来之后,其实公式的更改就很简单了。这篇paper也自建了一个网络RetinaNet [1] [ 1 ] ,在COCO数据集上的检测效果达到了40%的效果,提升效果非常明显。

这篇文章提出One-Stage网络检测精度较于Two-Stage网络差的原因主要是Class Imbalance,类别不均衡。
这个类别不均衡包括了一个数据集里面,
- 不同类的物体数量差距巨大(比如一个数据集里面每张图片车很多人很少);
- 同类物体的图片里前景和背景的数量差距巨大(比如一张图片本身很大,但是里面只有一个孤零零的小人);
- 样本与样本检测的难易(easy exampling 和 hard example,有些图片里面的人可能比较大很好检测,有些图片里的人比较小就难检测了);
等等,数据集自带的数据不平衡的弊端,会严重影响数据集训练出来的网络效果。
One-Stage的网络,会对每个图片预测出成千上万个备选框 (作者举例如DPMs,SSD等,但是Yolo好像不是这样啊。Yolo v1一共预测98个框子,Yolo v2倒是上千了。),备选框多了会导致两个问题。
1. 负例样本数远超正例样本数会导致网络训练不到足够的正例样本的特征,这使得训练没有什么效果。
2. 负例样本数量多,容易学习,会导致训练方向完全导向学习负例样本的方向。
这两个问题很好理解。其实就是负例样本贡献的loss太多,会把正例样本贡献的loss给淹没掉,所以模型训练就跑偏了。
为什么Two-Stage的网络就不会出这种问题呢?
因为它们在生成预测框的时候,首先控制了数量,其次控制了正负样例的比例,还有诸如OHEM等方法去控制样本难易程度等,所以就不会,详情见RCNN系列。
回到文章,那面对样本类别不均衡,难易不均衡的问题,应该如何解决呢?
Focal Loss Definition
作者的想法很简单:既然用的是不平衡的数据集,那么为什么要用平衡的loss函数呢?
首先给出公式。
其中,
这个公式有两个超参数,一个 α α ,一个 γ γ ,而 (1−pt)γ ( 1 − p t ) γ 被称为调制因子(modulating factor)。
为了方便起见,解释这个公式的时候,我们从二分类来举例。因为多分类里每一个类都是在二分类。
我们先定义 CE(pt)=−log(pt) C E ( p t ) = − l o g ( p t ) ,CE即cross entropy,其中 pt p t 的定义同上。选择 log l o g 函数的理由显而易见,首先在[0,1]间单调递减,其次始终为正值,最后p_t越小,loss大的程度越厉害,就像一个小孩回答问题错得越离谱,老师不仅打的板子多,每板子的重量还越大。
CE这个loss函数问题在于,很容易分类(即 pt>>0.5 p t >> 0.5 )的样例在数据集中的数量是不能忽略的,当易分类样例的数量太多,它们贡献出来的loss总和会覆盖掉那些特殊的难分类样例。
Balanced Cross Entropy
那么作个平衡?首先考虑一个样例分类的难易是和这个样例本身属于正负样例相关的。我们前面提到,由于数据集中正负样例比例相差太大,会导致模型学到后期学的大多是负样例的特征,因此区分负样例会很简单。所以为了遏制这种正负样例不均衡的情况,我们考虑增加一个系数 αt α t ,这个系数的计算公式如下,
可以想见,公式里的 α α 肯定是要在[0.5,1]之间的,原因很简单。我们现在的情况是正样例被负样例压过了,那么就导致正样例的 pt p t 值不太高(因为没学好),负样例的 pt p t 值很低(因为负样例的时候,log里面计算的是 1−pt 1 − p t )。所以为了抑制住负样例的loss贡献,我们给它乘上的系数肯定要比正样例的loss贡献所乘上的系数要小。反过来,如果是负样例被正样例压制了,那么 α α 则是在[0,0.5]之间。
Modulating Factor
论文同时指出,光有Balanced Cross Entropy是不够的,因为这样只是考虑了正负样本的均衡,而忽视了样本本身的难易之分,为了让模型更好的去学习难样本而不是选择忽略难样本,作者加入了一个称作调制系数的参数,即 (1−pt)γ ( 1 − p t ) γ 。这个系数是依靠一个样本的分类概率来判定这个样本分类的难易程度。概率越高,说明这个样本越容易分类。所以该样本提供的loss就应该越少。这是一个很直观的系数。而这个系数能够起到效果很好,如果概率是0.9,那么按照作者给的最优系数( γ=2 γ = 2 ),那么loss会降到原来的1/100,效果还是很好的。
所以最后公式就是,
还要提一点的是,文中给的最优超参数是: γ=2,α=0.25 γ = 2 , α = 0.25 ,为什么 α=0.25 α = 0.25 呢?好奇怪呀?分析原因应该是负样例由于分类简单,所以预测概率 p p 很低,那么 pt=1−p p t = 1 − p 就很高,所以调制系数会变得极低,这样的话反而变相的导致正样例压过了负样例,所以 αt α t 系数反向调节了一下。论文中虽然只尝试了几种值的组合,但是结果可以反映这一点的。

单纯只有 α α 系数的,最好的结果是 α=0.75 α = 0.75 。
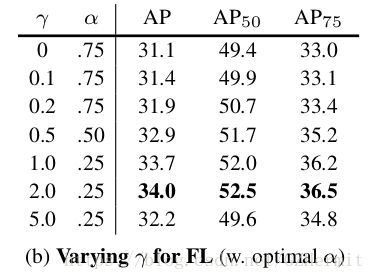
综合之后,最好的是 γ=2,α=0.25 γ = 2 , α = 0.25 。
RetinaNet
这个网络结构是作者为了验证自己的理论提出的网络结构。后面补充的时候介绍一下吧。

总结
这篇文章,是best paper,网上大家也是好评如潮,为什么呢?我觉得其实作者指出了一个在面对非均衡数据集的情况下很简单的一条解决问题的方法。
私以为目标检测想要增加精度,主要方法:
- 多尺度下目标特征的学习,增强模型对尺寸不变性的健壮程度
- 改变loss定义(这一点其实当初在做语义分割的时候一直在考虑怎么办,但完全没往这个方向想,想到另一个地方去了。现在突然感觉好像FL也可以用到语义分割上面啊)
- 增加对浅层特征的融合和学习,使得定位更加准确。
- 数据增强
目前脑子里面好像就这些了吧,文章看的太少,唉….