Kmeans以及优化的二分Kmeans

利用kmeans算法进行非监督分类

1.聚类与kmeans

• 引例:2004美国普选布什51.52% 克里48.48% 实际上，如果加以妥善引导，那么一有小部分人就会转换立场，那么如何找到这一小部分人以及如何在有限预算采取措施吸引他们呢？答案就是聚类(<<机器学习实战>>第十章)
• kmeans,k均值算法,属于聚类算法中的一种，属于非监督学习。
• 聚类中的一个重要的知识就是”簇”，简单说簇就是相似数据的集合，而在kmeans中主要是进行簇之间距离的运算，所以引入”质心”的概念，所谓质心就是代表这一簇的一个点(类比圆心)，由于簇中有很多点，那么质心的选取就是利用了”均值”，簇中所有点的平均值就是簇的质心，通过簇，一堆数据被分成k类，这就成了算法的名字“k均值”的直观解释.

2.kmeans伪代码以及思想

Kmeans是发现给定数据集的k个簇的算法，k是用户给定的。
主要工作流程伪代码如下

create k个点作为质心 (通常是随机选取)
while任意一个簇存在变化时
—— for 数据集中的数据点
——— for 每个质心
————- 计算质心到点的距离
————- 打擂台 找到最小的两者距离 记录id
——— 将数据点分配到最近的簇(打擂台记录了id)
—— 更新分配后的簇的质心(簇中所有点的均值)
返回质心列表以及分配的结果矩阵

3.二分-kmeans伪代码以及思想

主要思想
将每个簇一分为二 选取最小更新

伪代码
while 簇个数小于k
—— for 每个簇
———- 记录总误差
———- 在给定的簇上进行k=2的kmeans算法
———- 计算一分为二后的总误差
—— 选择最小误差的那个簇进行划分操作
返回簇以及分配情况

kmeans错误分类

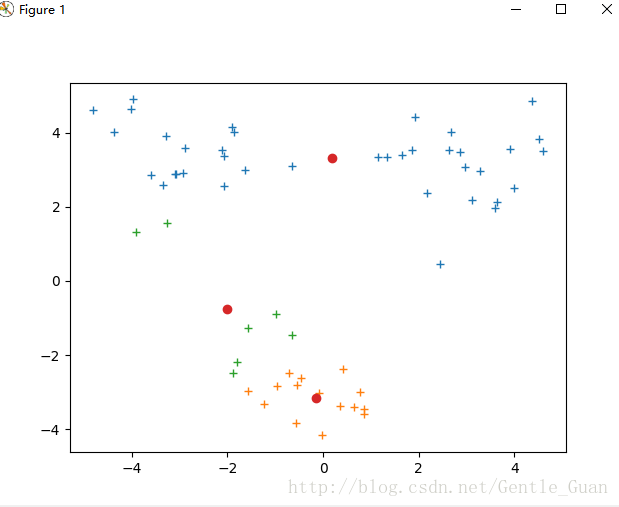
kmeans正确分类

二分-kmeans未翻车

 # -*- coding:utf-8 -*-

from numpy import *
import pylab as pl


# 读取二维坐标 存放在list中
def loadDataSet(fileName):
    dataMat = []
    with open(fileName, 'rb') as txtFile:
        for line in txtFile.readlines():
            init = map(float, line.split())
            dataMat.append(init)
    return dataMat


# 计算矩阵的欧氏距离 (两点间直线距离)
def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2)))


# 生成k个随机质心
def randCent(dataSet, k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k, n)))  # 生成k*n的二维mat矩阵
    for j in range(n):
        minJ = min(dataSet[:, j])
        rangeJ = float(max(dataSet[:, j]) - minJ)
        centroids[:, j] = minJ + rangeJ * random.rand(k, 1)  # 生成k*1的随机数
    return centroids


def Kmeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0]  # m行数据 m个点
    clusterAssment = mat(zeros((m, 2)))  # 分类结果
    centroids = createCent(dataSet, k)  # 类质心矩阵
    clusterChanged = True  # 簇不在变化 停止分类
    while clusterChanged:
        clusterChanged = False
        for i in range(m):  # 循环找最近的质心
            minDist = inf
            minIndex = -1
            for j in range(k):
                distJI = distMeas(centroids[j, :], dataSet[i, :]) # 第i个点与第j个质心的距离
                if distJI < minDist:  # 打擂台找最小值 记录下标(簇序号)
                    minDist = distJI
                    minIndex = j
            if clusterAssment[i, 0] != minIndex:  # 最小簇不是其所在簇
                clusterChanged = True  # 继续更新
            clusterAssment[i, :] = minIndex, minDist ** 2  # 更新簇序号 最小距离
        # print centroids
        for cent in range(k):  # 更新质心 nonzero返回非零矩阵
            nowInClust = dataSet[nonzero(clusterAssment[:, 0].A == cent)[0]]  # 得到这个簇里所有的点
            centroids[cent, :] = mean(nowInClust, axis=0)  # 按照列求均值 得到更新的质心坐标
    return centroids, clusterAssment


# pylab绘图
def printPic(inMat, Assment, centroids, k):
    for cent in range(k):
        pl.plot(inMat[Assment[:, 0] == cent, 0], inMat[Assment[:, 0] == cent, 1], '+')
    pl.plot(centroids[:, 0], centroids[:, 1], "o")
    pl.show()

# 二分kmeans(基于kmeans)
def binKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m, 2)))  # 分类结果 第i个实例 第j类 距离的平方
    centroid0 = mean(dataSet, axis=0).tolist()  # 初始质心
    centList = [centroid0]
    # 计算各点质心距离平方和
    for j in range(m):
        clusterAssment[j, 1] = distMeas(mat(centroid0), dataSet[j, :]) ** 2
    # 在未达到需要的质心之前进行--二分
    while (len(centList) < k):
        lowestSSE = inf  # 每次都为最大值
        for i in range(len(centList)):
         # 按照当前质心i分类 用来分配的点
            tempCluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0], :] 
            # 将当前质心所在类二分
            tempCentroidMat, tempSplitClusterAssment = Kmeans(tempCluster, 2, distMeas)  
            # 分配的点的sse和
            sseSplit = sum(tempSplitClusterAssment[:, 1])  
             # 其他未分配的点的sse和
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:, 0].A != i)[0], 1]) 
            if (sseNotSplit + sseSplit) < lowestSSE:
                bestCentToSplit = i
                bestNewCents = tempCentroidMat
                bestClustAss = tempSplitClusterAssment.copy()
                lowestSSE = sseSplit + sseNotSplit

        # 更新分类
        # 0 1 2 新分类的(1) 就是 0 1  2 (3)
        bestClustAss[nonzero(bestClustAss[:, 0].A == 1)[0], 0] = len(centList)  
        # 0 1 2 新分类的(0) 就是 0 1 (2)
        bestClustAss[nonzero(bestClustAss[:, 0].A == 0)[0], 0] = bestCentToSplit  
        # 更新质心
        centList[bestCentToSplit] = bestNewCents[0, :].tolist()[0]
        centList.append(bestNewCents[1, :].tolist()[0])  # 把两个质心加上
        # 更新距离
        # 原来的tosplit更新为两点
        clusterAssment[nonzero(clusterAssment[:, 0].A == bestCentToSplit)[0], :] = bestClustAss       
    return mat(centList), clusterAssment


if __name__ == "__main__":
    data = loadDataSet("testByGpx.txt")
    centroids, assment = binKmeans(array(data), 2)
    printPic(array(data), array(assment), array(centroids), 2)

'testByGpx 简单测试数据如下'
'''
1 1
2 1
4 5
5 6
'''