R 分析两个变量

ggplot2：数据分析与图形艺术- Hadley Wickham

8 过度绘制和领域知识

每用户都有一定的朋友数，x是实际的看的人数的百分比，y是猜想的看的人数的百分比。

9 条件均值

install.packages('dplyr')
library(dplyr)

# 其中的常见函数
filter()
group_by()
mutate()
arrange()

更多关于 dplyr 包的信息
Hadley Wickham 于 2014 年在 useR 公布的教程：
dplyr 简介
dplyr 教程（第 1 部分）
dplyr 教程（第 2 部分）

12 相关性

# 方法一
cor.test(pf$age, pf$friend_count, method = "pearson")
# 方法二
with(pf, cor.test(age, friend_count, method = "pearson"))


Pearson's product-moment correlation

data:  pf$age and pf$friend_count
t = -8.6268, df = 99001, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.03363072 -0.02118189
sample estimates:
        cor 
-0.02740737 

pearson product-moment correlation
pearson 积矩关联

绝对值0.3左右，代表两者之间是相关性比较弱；0.5左右代表相关性较强，0.7左右相关性很强。

13 子集、相关性

# 某个子集 的 相关系数
with(subset(pf, age <= 70), cor.test(age, friend_count))

tip：相关 不代表 因果，需要从实验性研究中获取数据，然后使用推论统计学来得出因果关系，而不是描述性统计学。

14 相关分析法

R Tutorial - Correlation Coefficient
相关分析法: Pearson’s r, Spearman’s ρ 及 Kendall’s τ

15 创建散点图

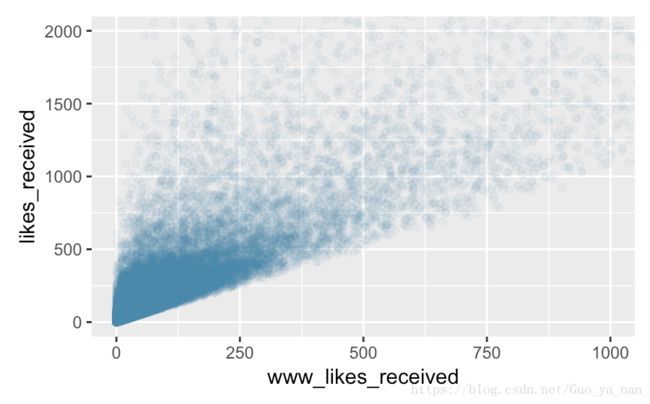
ggplot(aes(x = www_likes_received, y = likes_received), data = pf) +
  geom_point(alpha = 1/20, 
             color = "steelblue") +
  coord_cartesian(xlim = c(0, 1000), ylim = c(0, 2000))

16 强相关

with(pf, cor.test(www_likes_received, likes_received))


    Pearson's product-moment correlation

data:  www_likes_received and likes_received
t = 937.1, df = 99001, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.9473553 0.9486176
sample estimates:
      cor 
0.9479902 

相关系数在 X 或 Y 的线性转换下是不变的，并且当 X 和 Y 都被转换为 z 分数时，回归线的斜率就是相关系数。

17 对于相关性的研究

对facebook的研究，用户在过去一个月内更新多少状态，与很多变量强相关，比如 过去一个月内登录的天数，好友的个数，过去一个月内上传的照片数。所有这些变量都高度相关，因为它们衡量的东西都差不多，就是用户的互动频率。

通常在开始一项研究之前，做一些回归建模会很有帮助，看看变量之间是相互独立的还是相关的，可以帮助决定保留、舍弃哪些变量。

18 参数的传递

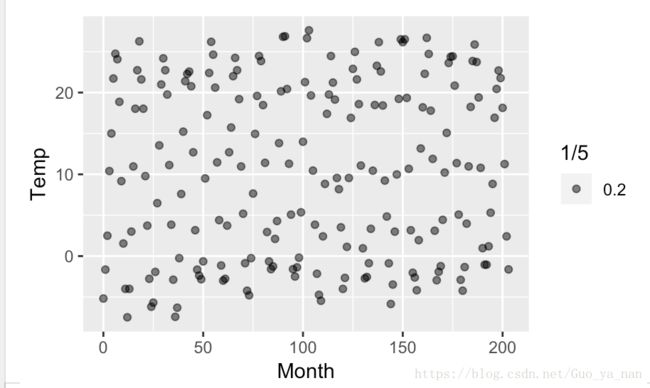
ggplot(aes(x = Month, y = Temp), data = Mitchell) + 
  geom_point(alpha = 1/5)

qplot(data = Mitchell, Month, Temp, alpha = 1/5)

qplot 中除了精确匹配之外，剩下的 Month, Temp按照字母顺序传递参数给x，y。

21 数据可视化

数据可视化先驱：John Tukey，William Playfair
William Playfair 和图形心理学
数据的本质应该暗示图形的形状。

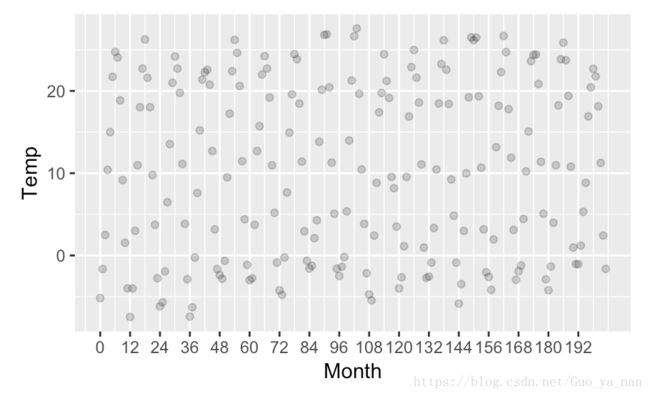
library(alr3)
data("Mitchell")

ggplot(data = Mitchell, aes(x = Month, y = Temp)) +
  geom_point(alpha = 1/5) +
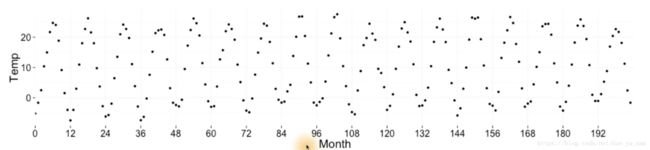
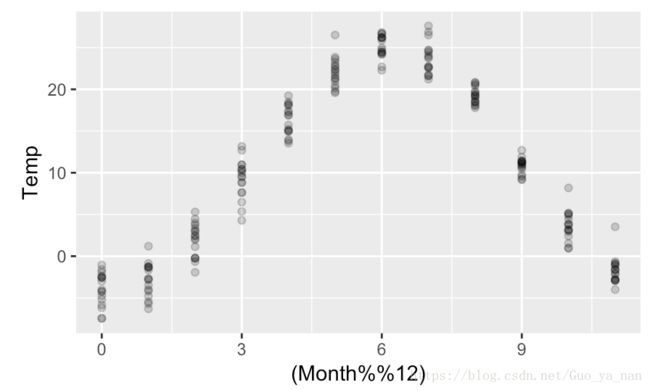
  scale_x_continuous(breaks = seq(0, 203, 12))

ggplot(data = Mitchell, aes(x = (Month%%12), y = Temp)) +
  geom_point(alpha = 1/5)

22 了解噪声：年龄到月龄

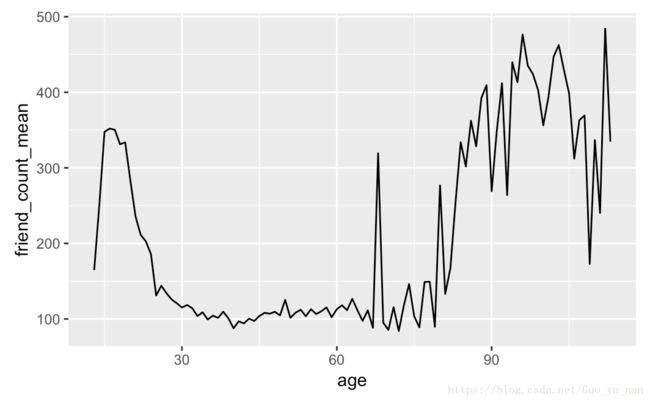
ggplot(aes(x = age, y = friend_count), data = pf) +
  geom_line(stat = "summary", fun.y = mean)

ggplot(aes(x = age, y = friend_count_mean), data = pf.fc_by_age) + geom_line()

pf$age_with_months <- pf$age + (1 - pf$dob_month/12)

pf$age_with_months <- with(pf, age + (1 - dob_month / 12))

23 带有月均值的年龄

# 方法一
age_months_groups <- group_by(pf, age_with_months)
pf.fc_by_age_months <- summarise(age_months_groups,
                          friend_count_mean = mean(friend_count),
                          friend_count_median = median(friend_count),
                          n = n())
pf.fc_by_age <- arrange(pf.fc_by_age, age)
# 以下可以省略，以上得到的即为排序后的结果
pf.fc_by_age_months <- arrange(pf.fc_by_age_months2, age_with_months)

> head(pf.fc_by_age_months)
# A tibble: 6 x 4
  age_with_months friend_count_mean friend_count_median     n
                                         
1            13.2              46.3                30.5     6
2            13.2             115.                 23.5    14
3            13.3             136.                 44      25
4            13.4             164.                 72      33
5            13.5             131.                 66      45
6            13.6             157.                 64      54

# 方法二
library(dplyr)

pf.fc_by_age_months2 <- pf %>%
  group_by(age_with_months) %>%
  summarise(friend_count_mean = mean(friend_count),
            friend_count_median = median(friend_count),
            n = n()) %>%
  arrange(age_with_months)

24 条件均值中的噪声

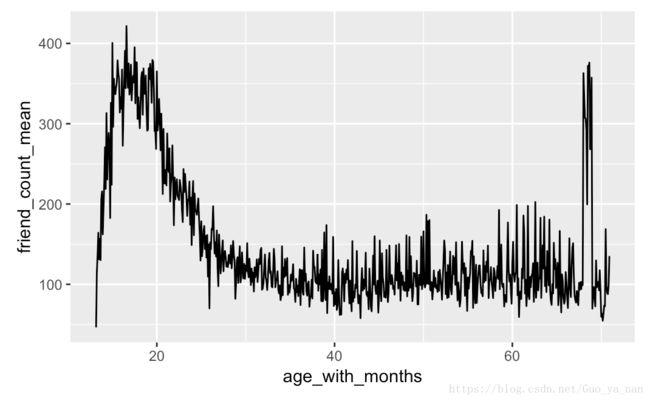
# 以上结果进行 画图
ggplot(data = subset(pf.fc_by_age_months, age_with_months < 71), aes(x = age_with_months, y = friend_count_mean)) + 
  geom_line()

25 平滑化条件均值

p1 <- ggplot(aes(x = age, y = friend_count_mean),
            data = subset(pf.fc_by_age, age < 71)) + 
  geom_line()

p2 <- ggplot(aes(x = age_with_months, y = friend_count_mean),
             data = subset(pf.fc_by_age_months, age_with_months < 71)) +
  geom_line()

library(gridExtra)
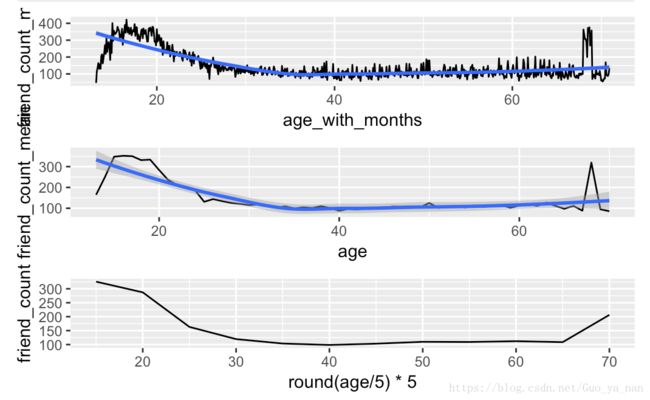
grid.arrange(p2, p1, ncol = 1)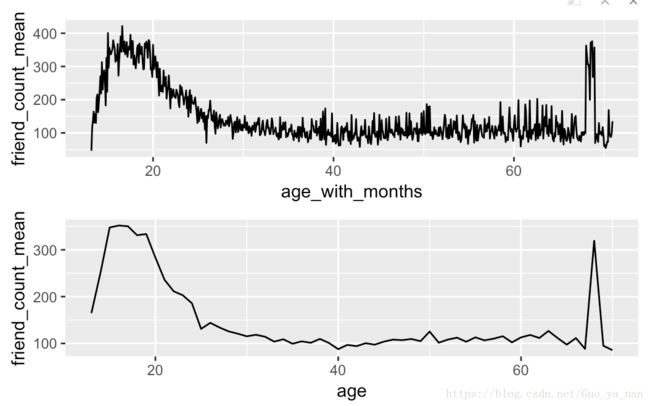

第一幅图采用了更精细的分组，噪声更多。增加分组，能够让图形变得更平滑。

p1 <- ggplot(aes(x = age, y = friend_count_mean),
            data = subset(pf.fc_by_age, age < 71)) + 
  geom_line() +
  geom_smooth()

p2 <- ggplot(aes(x = age_with_months, y = friend_count_mean),
             data = subset(pf.fc_by_age_months, age_with_months < 71)) +
  geom_line() +
  geom_smooth()

# 此处代码没看懂
p3 <- ggplot(aes(x = round(age / 5) * 5, y = friend_count),
             data = subset(pf, age < 71)) + 
  geom_line(stat = "summary", fun.y = "mean")
grid.arrange(p2, p1, p3, ncol = 1)

最后一段代码没懂

局部回归 (LOESS) 的直观解释
Local regression的wiki解释

27 总结

散点图
在散点图的基础上增加 条件汇总（比如 平均值，百分位数）
相关系数
调整可视化效果：设置透明度，抖动，变换坐标轴，温度数据的月份调整。