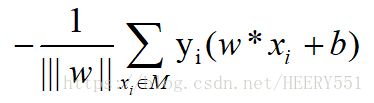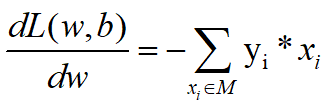统计学习方法_2感知机_学习笔记_python实现

一、感知机模型

感知机由输入到输出（+1，-1）空间的模型为：

                                                     

                        其中w、b均为感知机的模型参数，w为权值或权值向量，b为偏置

                        sign是符号函数，即sign(x) 在x>=0时取+1，在x<0时取 -1.

感知机是一个线性分类模型，对于线性方程        w是超平面法向量、b是超平面截距。

二、感知机分类原理

（1）数据集的线性可分性

    数据集线性可分

既可以将正负实例均可分到超平面的两侧，即对于所有  的实例i 均有 ，而对于 的实例i均拥有，那么数据集即可分，否则不可分。

（2） 分类的原理

    感知机分类是一个不断学习的过程，也就是不断的减小误分类的点的数目使得损失函数减小的过程。而其测量尺度即为通过计算所有误分类点到超平面的距离总和。其中输入的任何点到超平面的距离为

                                                                                     其中||w|| 是w的L2 范数

由（1）之可知 正确分类为     而误分类则为     

因此所有误分类点到超平面的距离为： 

                                                

此处忽略    记得到了感知机的损失函数 ，即

                                               

分类的原理其实就是能够不断的使我们的损失函数达到最小，达到0是最佳的，接下来的即为感知机的算法，就是不断学习，让感知机的损失函数达到最小。

三、感知机的学习算法

      优化的方法即为随机梯度下降法

（1）原始形式

    随机梯度下降，即任意选择一个超平面的w0、b0，其次使用随机梯度进行极小化目标函数。

    其中损失函数 梯度 为

    

     

再随机给出一个误分类点  ,对其w、b进行参数更新

                   

                    

        其中   是一个更新步长，也成为学习率，不断学习更新参数后，即可使得损失函数不断减小，直到为0.

算法具体步骤如下

可以发现  原始形式中，更新的参数分别为权重w与截距b 

应用如下

其中手工解法如书上所示，而python实现代码如下：

#!/usr/bin/env python3
# -*- coding: UTF-8 -*-
# 参考博客：https://blog.csdn.net/winter_evening/article/details/70196040

import matplotlib.pyplot as plt
import numpy as np

def train(train_datas,steplong):
    w=[0,0]
    b = 0
    #  第一个列表依次选择的误分类点事 x1，x3，x3，x3，x1，x3，x3，x3      【w，b  （【1,1】，-3）】
    #  第二个列表依次选择的误分类点事 x1，x3，x3，x3，x2，x3，x3，x3，x1，x3，x3，x3  【w，b  （【2,1】，-5）】
    x_list = [train_datas[0], train_datas[2], train_datas[2], train_datas[2], train_datas[0], train_datas[2], train_datas[2]]
    # x_list = [train_datas[0],train_datas[2],train_datas[2],train_datas[2],train_datas[1],train_datas[2],train_datas[2],train_datas[2],train_datas[0],train_datas[2],train_datas[2]]
    for x in x_list:
        x1,x2,y=x
        if (y*(w[0]*x1+w[1]*x2+b)<=0):
            w[0]+=steplong*y*x1
            w[1]+=steplong*y*x2
            b += steplong*y
    return w,b

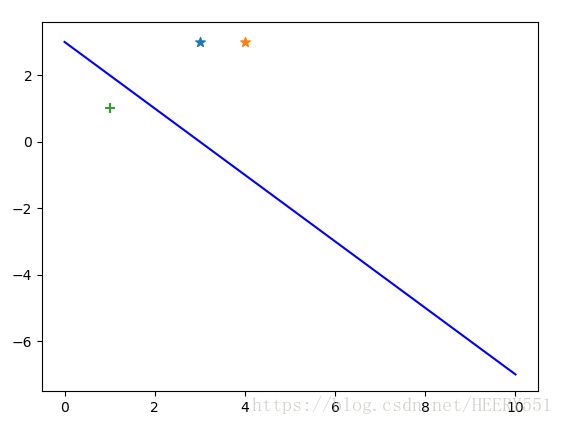
def plot_point(train_datas,w,b):              # 画图函数
    plt.figure()
    x1 = np.linspace(0,10,100)                 # 选择范围【0-10】
    x2 = (-b-w[0]*x1)/w[1]                    #  0 = b+w[0]*x1+w[1]*x2  ==>  x2
    plt.plot(x1,x2,color = 'b')

    for i in range(len(train_datas)):
        if (train_datas[i][-1]==1):         # 画正例点
            plt.scatter(train_datas[i][0],train_datas[i][1],marker='*',s=50)
        else:                               # 画反例点
            plt.scatter(train_datas[i][0],train_datas[i][1],marker='+',s=50)
    plt.show()

if __name__ == '__main__':
    train_data1 = [[3,3,1],[4,3,1]]
    train_data2 =[[1,1,-1]]
    train_datas = train_data1+train_data2
    w,b = train(train_datas,1)
    plot_point(train_datas,w,b)
    print(w,b)

而程序运行结果如下：

   

取另外一组误分类点所得结果:

 

原始形式总结：感知机学习算法存在许多解，这些解既依赖于初值的选择、也依赖于迭代过程中误分类点的选择顺序。

（2) 对偶形式

    基本思路：将w、b表示为 实例  xi 和标记yi的线性组合形式，通过求解其系数而求得w和b，不失一般性，也可将初始值 与 均为0, 

   

      其中 ni表示第i个样本的学习次数

    对偶形式的算法步骤如下所示

        

由上述算法步骤可知，我们每次更新的内容是    与  值，到最后的时候，再通过 及训练样本数求解出权重w，而手工算法如书上所示，python实现该例的代码如下：

#!/usr/bin/env python3
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt

def train(train_datas,step_long):                      # 训练函数
    w = [0,0]                                          # 初始化权重
    b = 0
    alpha = np.zeros(len(train_datas)).T              # 初始化alpha 长度与训练数据个数相同
    data_array = np.array(train_datas)                # 将训练列表数据转换为numpy的矩阵形式
    gram = np.matmul(data_array[:,:-1],data_array[:,:-1].T)   # 计算gram 矩阵
                                         # 误分类点选择的顺序不同，最后的分类超平面方程也不同
    i_list = [0,2,2,2,0,2,2]            # 选择误分类点的顺序列表【x1,x3,x3,x3,x1,x3,x3】
    #i_list = [0,2,2,2,1,2,2,2,0,2,2]   # 【x1,x3,x3,x3,x2,x3,x3,x3,x1,x3,x3】
    for k in i_list:
        i = k
        xi = data_array[i,:-1]
        yi = data_array[i,-1]
        temp = 0
        for j in range(len(train_datas)):
            temp += alpha[j]*data_array[j,-1]*gram[i][j]
        if (yi*(temp+b)<=0):             # 出现误分类
            alpha[i] += step_long        # 更新对应位置的alpha
            b += yi*step_long            # 更新 b的值
    for j in range(len(train_datas)):   # 求出最后的权重
        w += alpha[j]*data_array[j,-1]*data_array[j,:-1]
    return w,b,alpha,gram

def plot_points(train_datas,w,b):        # 画图函数
    plt.figure()
    x1 = np.linspace(0,8,100)
    x2 = (-b-w[0]*x1)/(w[1]+1e-10)
    plt.plot(x1,x2,color = 'r')

    for i in range(len(train_datas)):
        if (train_datas[i][-1]==1):
            plt.scatter(train_datas[i][0],train_datas[i][1],marker = '*',s=50)
        else:
            plt.scatter(train_datas[i][0],train_datas[i][1],marker='x',s=50)
    plt.show()

if __name__ == '__main__':
    train_data1 = [[3,3,1],[4,3,1]]
    train_data2 = [[1,1,-1]]
    train_datas = train_data1+train_data2
    w,b,alpha,gram = train(train_datas,1)
    plot_points(train_datas,w,b)
    print(w)
    print(b)
    print(alpha)
    print(gram)

运行结果如下：

运行另一个误分类选择顺序，结果如下所示：

至此，对偶形式算法结束。

总结：感知机是根据输入实例的特征向量x，对其进行二类分类的线性分类模型，其分类原理是不断减小损失函数，使其最后为0时无误分类，而度量损失函数的是所有误分类点到分离超平面的距离之和。其学习算法是基于随机梯度下降算法，其次对损失函数进行最优化，优化形式主要有原始形式与对偶形式，原始形式中，首先任意选取一个超平面，再此取梯度下降优化目标函数，而这个过程中，一次随机选择一个误分类点使其下降。如果感知机中的数据集线性可分，那么感知机学习算法是收敛的，并且其存在无数的解，而由于解的初值或不同的迭代顺序而可能有所不同。

参考：https://blog.csdn.net/winter_evening/article/details/70196040