8、【李宏毅机器学习（2017）】Keras

上一篇博客介绍了反向传播算法的理论部分，这一篇博客将利用python的模块Keras开始神经网络算法的实战。

---

目录

---

Keras介绍

常用的神经网络模块还包括TensorFlow和Theano，这两个模块有着高度的灵活性，可定制化程度极高，可以理解为一个微分器，学习难度大，Keras是TensorFlow和Theano的interface，使用Keras是在调用TensorFlow，并且也有着一定的灵活性，且学习难度低。

Keras使用

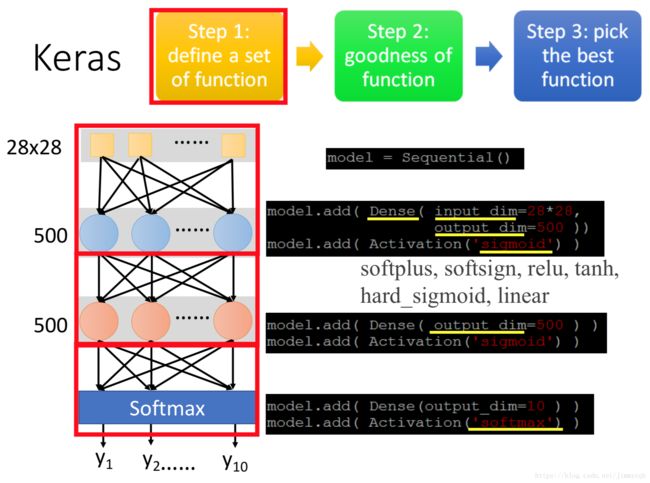
step1

keras的使用按照神经网络层次逐一添加神经层，

import keras
from keras.layers import Activation, Dense
from keras import Sequential

#定义一个神经网络类
model = Sequential()

#添加第一个隐藏层，输入的参数是28*28维，第一层神经元个数为500，激活函数全部设置为‘sigmoid’
model.add(Dense(input_dim=28*28,output_dim=500))
model.add(Activation('sigmoid'))

#添加第二个隐藏层，设置第二层神经元个数也为500，激活函数全部设置为‘sigmoid’
model.add(Dense(output_dim=500))
model.add(Activation('sigmoid'))

#添加输出层，输出参数是10维，激活函数全部设置为多分类函数‘softmax’
model.add(Dense(output_dim=10))
model.add(Activation('softmax'))

step2

定义神经网络模型的选择标准，设置梯度下降的算法。

#使用categorical_crossentropy交互熵作为模型选择的标准，梯度下降的算法为'adam'
model.compile(loss='categorical_crossentropy',optimizer='adam',metrics=['accuracy'])

step3

利用训练集数据拟合模型，按照step2设置的标准选择最优模型。

#训练模型
model.fit(x_train,y_train,batch_size=100,nb_epoch=20)

使用keras模型进行预测

#计算模型的预测效果
score=model.evaluate(x_test,y_test)
print('Total loss on Testing Set:',score[0])
print('Accuracy of Testing Set:',score[1])

#预测测试集
result = model.predict(x_test)

神经网络中参数

batch_size与nb_epoch介绍

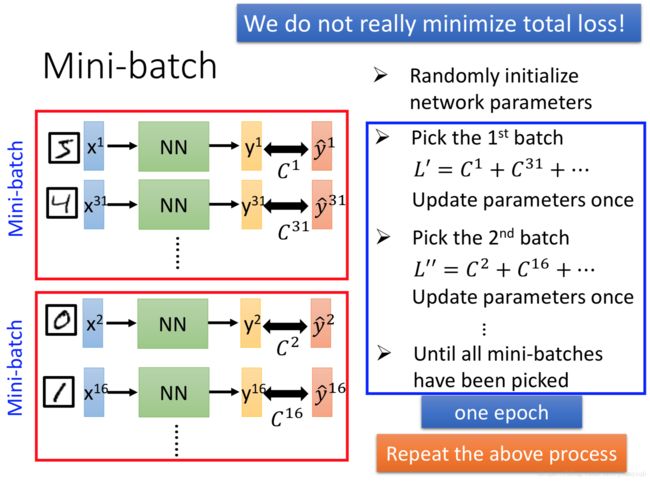
在实际运算中神经网络并不是极小化Total Loss，而是将训练集数据随机分成一个一个的Mini-batch，随机选择一个batch（比如batch1），使用这一个batch里的所有数据拟合模型，更新参数，如此循环进行直到使用过所有的batch，这个过程称为一次epoch。

神经网络模型中的参数与Keras中函数参数的对应关系如下：

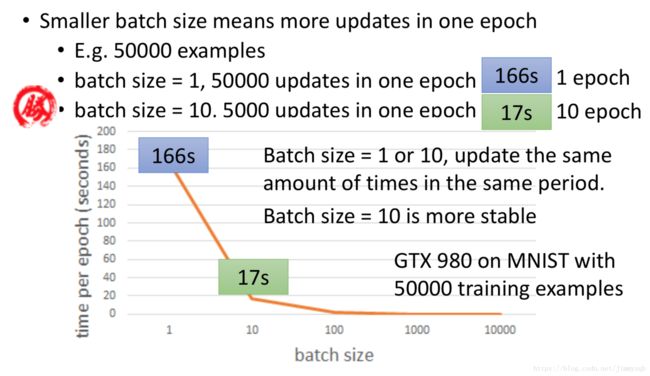
batch_size不同大小对计算耗时的影响

现在对比同样计算50000次不同算法的系统耗时：

• batch size取1，epoch取50000次（相当于随机梯度下降）
• batch size取10，epoch取5000次
  

batch_size不同大小对计算的影响原因

现在选取两个样本（黄色、绿色）进行分析，在随机梯度下降算法中，z通过两次运算得到，而在Mini-batch中只要一次矩阵运算即可得到相同的结果，理论上两者的计算量是一样的，但是由于GPU的作用，一次后者计算的时间和一次前者计算的时间一样，因此后者计算的总时间等于前者计算的总时间的一半。

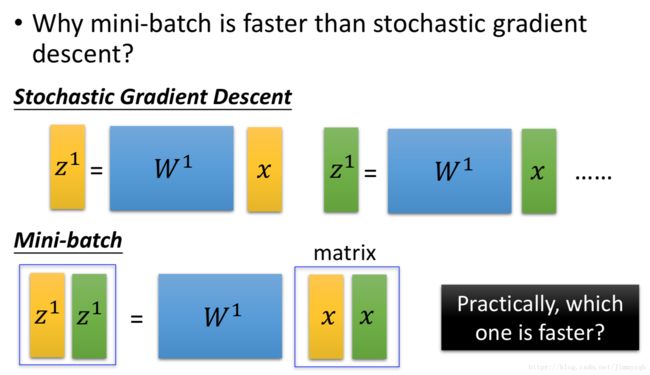
尽管batch size设置大一些越能调动GPU的性能，但是实际运用中batch size并不是越大越好：

• batch size太大容易得到局部最优解（神经网络中的Loss function函数并不是像线性回归中的严格凸函数，而是坑坑洼洼的函数，很容易得到局部最优解，增加随机性比较容易“跳出”局部最优解的点）
• batch size太大会超过GPU的最大并行计算能力，因此太大的batch size并不能提高计算速度

Keras2.0

keras的版本更新使得原先的函数有部分参数发生变化，现在使用新的keras模块重新编写之前的神经网络模型。

#定义一个神经网络类
model = Sequential()

#添加第一个隐藏层，输入的参数是28*28维，第一层神经元个数为500，激活函数全部设置为‘sigmoid’
model.add(Dense(input_dim=28*28,units=500,activation='sigmoid'))

#添加第二个隐藏层，设置第二层神经元个数也为500，激活函数全部设置为‘relu’
model.add(Dense(units=500,activation='relu'))

#添加输出层，输出参数是10维，激活函数全部设置为多分类函数‘softmax’
model.add(Dense(ounits=10,activation='softmax'))

#使用categorical_crossentropy交互熵作为模型选择的标准，梯度下降的算法为'adam'
model.compile(loss='categorical_crossentropy',optimizer='adam',metrics=['accuracy'])

#训练模型
model.fit(x_train,y_train,batch_size=100,nb_epoch=20)

#计算模型的预测效果
score=model.evaluate(x_test,y_test)
print('Total loss on Testing Set:',score[0])
print('Accuracy of Testing Set:',score[1])

#预测测试集
result = model.predict(x_test)

Keras实战

from keras.optimizers import SGD,Adam
from keras.utils import np_utils
from keras.datasets import mnist

def load_data():
    (x_train,y_train),(x_test,y_test)=mnist.load_data()
    #用于训练的样本量
    number = 10000
    x_train = x_train[0:number] #(10000, 28, 28)
    y_train = y_train[0:number] #(10000, )

    #将一张图的2维数据转化为1维数据
    x_train = x_train.reshape(number,28*28)
    x_test = x_test.reshape(x_test.shape[0],28*28)

    #转换int数据类型为float数据类型
    x_train = x_train.astype('float32')
    x_test = x_test.astype('float32')

    #转换int数据类型为categorical数据类型
    y_train = np_utils.to_categorical(y_train,10)
    y_test = np_utils.to_categorical(y_test,10)

    x_train = x_train/255
    x_test = x_test/255

    return (x_train,y_train),(x_test,y_test)

(x_train,y_train),(x_test,y_test) = load_data()
x_train.shape # (10000, 784)
y_train.shape # (10000, 10)

model = Sequential()
model.add(Dense(input_dim=28*28,units=500,activation='sigmoid'))
model.add(Dense(units=500,activation='sigmoid'))
model.add(Dense(units=500,activation='sigmoid'))
model.add(Dense(units=10,activation='softmax'))

model.compile(loss='mse',optimizer=SGD(lr=0.1),metrics=['accuracy'])
model.fit(x_train,y_train,batch_size=100,nb_epoch=20)

#计算模型的预测效果
score=model.evaluate(x_test,y_test)
print('Total loss on Testing Set:',score[0]) #0.0899
print('Accuracy of Testing Set:',score[1])  #0.1089

预测结果准确率0.1089，大致就等于10个数里瞎猜一个，在下一篇博客将对模型进行优化。