【机器学习】基于AutoEncoder的BP神经网络的tensorflow实现

一、基于AutoEncoder的BP神经网络

1.1、BP神经网络

1.1.1、BP神经网络结构

设有数据集$\left\{\left(X_1,Y_1\right),\left(X_2,Y_2\right),\cdots ,\left(X_m,Y_m\right)\right\}$，每个样本特征有$n$个特征，即$X_i=\left\{x_1,x_2,\cdots ,x_n\right\}$，对应的样本标签为$Y_i=\left\{o_1,\cdots ,o_j\right\}$。

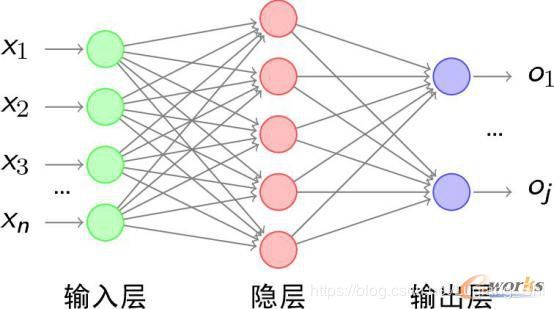
BP神经网络的结构图如上所示。BP神经网络是三层结构：输入层、隐含层和输出层。

输入层：节点数等于样本的特征维度数$n$，输入每一个样本的特征。
隐含层：节点数可以根据需要设置（本博文中设为k）。
输出层：节点数等于标签维度数$j$。

输入层到隐含层之间的权重矩阵$W_1$，偏置$b_1$，$W_1$的维度为$n\ast k$，$b_1$的维度为$1\ast k$；隐含层到输出层之间的权重矩阵$W_2$，偏置$b_2$，$W_2$的维度为$k\ast j$，$b_2$的维度为$1\ast j$。
本博文中隐含层和输出层的节点激活函数为sigmoid函数。

1.1.2、BP神经网络的训练

前向传播求误差：
对于样本$X_i$。
隐含层的输入：$H_{in}=X_i\cdot W_1+b_1$
隐含层的输出：$H_{output}=sigmoid\left(H_{in}\right)$
输出层的输入：$O_{in}=H_{output}\cdot W_2+b_2$
输出层的输出：$O_{output}=sigmoid\left(O_{in}\right)$
反向传播训练模型参数：
本博文采用tensorflow的tf.Session()入口训练模型参数，tensorflow模型构建与训练的流程方法可参考本人之前的博文。

1.2、AutoEncoder（自编码器）

上面提到的基础的BP神经网络中输入层到隐含层的权值是随机设置的，如果权值的初始值与模型的最优权值相差较远，需要大量的迭代训练才能得到最优参数。如何合理地给权值设定初始值，减少模型训练时的迭代。

AutoEncoder是将输入向量经过权重$W_1$和偏置$b_1$映射到隐含层上，隐含层到输出层的权重矩阵$W_2$为$W_1$的转置矩阵，损失函数为网络输出与输入向量的欧式距离（参考资料【1】）。

可以将输入层到隐含层理解为编码过程，隐含层到输出层理解为解码过程。

基于AutoEncoder的BP神经网络，输入层到隐含层的初始权值矩阵和偏置为AutoEncoder训练好的权重$W_1$和$b_1$。

二、基于AutoEncoder的BP神经网络的tensorflow实现

tensorflow代码地址：https://github.com/shiluqiang/BP_NN_tensorflow
本博文代码参考（资料【2】）
首先利用AutoEncoder训练输入层到隐含层权重和偏置。

class Denoising_AutoEncoder():
    def __init__(self,n_hidden,input_data,keep_prob):
        '''类参数定义
        '''
        self.W = None  #输入层到隐含层的权重
        self.b = None  #输入层到隐含层的偏置
        self.encode_r = None #隐含层输出
        self.n_hidden = n_hidden #隐含层节点数
        self.input_data = input_data #输入样本
        self.keep_prob = keep_prob #特征保持不变的比例
        self.W_eval = None #权重W的值
        self.b_eval = None #偏置b的值
    
    def fit(self):
        '''降噪自编码器训练
        '''
        # 1.创建输入输出占位符和参数变量
        #输入层节点个数
        n_visible = (self.input_data).shape[1]
        #输入数据占位符
        X = tf.placeholder('float',[None,n_visible],name = 'X')
        #用于将部分输入数据置为0
        mask = tf.placeholder('float',[None,n_visible],name = 'mask')
        #创建输入层到隐含层的权重和偏置
        W_init_max = 4.0 * np.sqrt(6.0 / (n_visible + self.n_hidden))
        W_init = tf.random_uniform(shape = [n_visible,self.n_hidden], minval = - W_init_max, maxval = W_init_max)
        self.W = tf.Variable(W_init,name = 'W')  #输入层到隐含层权重
        self.b = tf.Variable(tf.zeros([self.n_hidden]), name = 'b')
        #隐含层到输出层的权重和偏置
        W_prime = tf.transpose(self.W)
        b_prime = tf.Variable(tf.zeros([n_visible]), name = 'b_prime')
        # 2.构建前向传播的计算图
        #信号前向传播
        tilde_X = mask * X #对输入样本加入噪音        
        Y = tf.nn.sigmoid(tf.matmul(tilde_X,self.W) + self.b)
        Z = tf.nn.sigmoid(tf.matmul(Y,W_prime) + b_prime)  
        # 3.声明损失函数和优化算法
        #损失函数(均方误差)
        cost = tf.reduce_mean(tf.pow(X - Z,2))
        #最小化损失函数
        train_op = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
        #导入样本数据
        trX = self.input_data
        # 4.反向传播求参数
        with tf.Session() as sess:
            #初始化所有参数
            tf.global_variables_initializer().run()
            for i in range(30):
                for start,end in zip(range(0,len(trX),128),range(128,len(trX) + 1,128)):
                    input_ = trX[start:end] # 输入
                    mask_np = np.random.binomial(1,self.keep_prob,input_.shape) # 设置mask
                    sess.run(train_op, feed_dict = {X: input_, mask: mask_np})
                if i % 5 == 0:
                    mask_np = np.random.binomial(1,1,trX.shape)
                    print('Loss function at step %d is %s'%(i,sess.run(cost,feed_dict = {X: trX, mask: mask_np})))
            #保存输入层到隐含层的权重和偏置，保存隐含层的输出
            self.W_eval = (self.W).eval()
            self.b_eval = (self.b).eval()           
            mask_np = np.random.binomial(1,1,trX.shape)
            self.encode_r = Y.eval({X: trX, mask: mask_np})
    
    #获得参数
    def get_value(self):
        
        return self.W_eval,self.b_eval

然后，构造BP神经网路并训练参数。

class Denosing_AutoEncoder_NN():
    def __init__(self,hidden_nodes,keep_prob,input_data_trainX,input_data_trainY,input_data_testX,input_data_testY):
        self.hidden_nodes = hidden_nodes #隐含层节点数
        self.keep_prob = keep_prob # 特征保持不变的比例
        self.input_data_trainX = input_data_trainX #训练样本的特征
        self.input_data_trainY = input_data_trainY #训练样本的标签
        self.input_data_validX = input_data_trainX #验证样本的特征
        self.input_data_validY = input_data_trainY #验证样本的标签
        self.input_data_testX = input_data_testX #测试样本的特征
        self.input_data_testY = input_data_testY #测试样本的标签
        
    def fit(self):
        # 1.训练降噪自编码器获得输入层到隐含层的初始权重与偏置
        data_train = self.input_data_trainX
        dae = Denoising_AutoEncoder(self.hidden_nodes,data_train,self.keep_prob)
        dae.fit()
        W1_DA,b1_DA = dae.get_value()
        # 2. 生命输入输出的占字符
        n_input = (self.input_data_testX).shape[1]
        n_output = (self.input_data_testY).shape[1]
        X = tf.placeholder('float',[None,n_input],name = 'X')
        Y = tf.placeholder('float',[None,n_output],name = 'Y')
        # 3.参数变量设置
        #输入层到隐含层参数
        W1 = tf.Variable(W1_DA,name = 'W1')
        b1 = tf.Variable(b1_DA,name = 'b1')
        #隐含层到输出层参数
        W2 = tf.Variable(tf.truncated_normal([self.hidden_nodes,n_output],stddev = 0.1),name = 'W2')
        b2 = tf.Variable(tf.constant(0.1,[1,n_output]),name = 'b2')
        # 4.构建前向传播的计算图
        H = tf.nn.sigmoid(tf.matmul(X,W1) + b1)  #隐含层输出
        y_pred = tf.nn.sigmoid(tf.matmul(H,W2) + b2) #输出层输出
        # 5.生命代价函数和优化算法
        cost = tf.reduce_mean(tf.pow(Y - y_pred,2))
        train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
        
        model_predictions = tf.argmax(y_pred,1)
        correct_predictions = tf.equal(model_predictions,tf.argmax(Y,1))
        accuracy = tf.reduce_mean(tf.cast(correct_predictions,'float'))
        # 6.反向传播参数微调
        trX = self.input_data_trainX
        trY = self.input_data_trainY
        vaX = self.input_data_validX
        vaY = self.input_data_validY
        teX = self.input_data_testX
        teY = self.input_data_testY
        
        with tf.Session() as sess:
            tf.global_variables_initializer().run()
            for i in range(50):
                for start,end in zip(range(0,len(trX),128),range(128,len(trX) + 1,128)):
                    sess.run(train_step, feed_dict = {X: trX[start:end],Y: trY[start:end]})
                if i % 5.0 == 0:
                    print('Accuracy at step %s on validation set:%s'%(i,sess.run(accuracy,feed_dict={X:vaX,Y:vaY})))
            print('Accuracy on test set is :%s'%(sess.run(accuracy,feed_dict={X:teX,Y:teY})))

参考资料

1、https://blog.csdn.net/google19890102/article/details/49738323
2、《python机器学习算法》