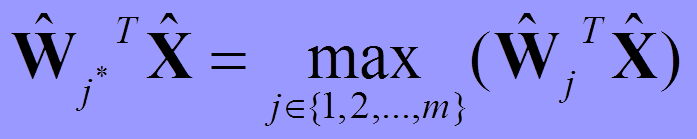SOM网络(Kohonen自组织网络)学习第二篇
转自:http://blog.csdn.net/xbinworld/article/details/50818803,其实内容更多的是百度文库里叫《SOM自组织特征映射神经网络》这篇文章上的,博主增加了一些理解。
本文详细介绍一下自组织神经网络概念和原理,并重点介绍一下自组织特征映射SOM网络。SOM和现在流行的ANN(MLP)模型在结构上类似,都由非常简单的神经元结构组成,但是SOM是一类“无监督学习”模型,一般的用法是将高维的input数据在低维的空间表示[1],因此SOM天然是一种降维方法。除了降维,SOM还可以用于数据可视化,以及聚类等应用中。
1、背景:自组织(竞争型)神经网络
SOM是一种自组织(竞争型)神经网络,除了SOM外,其他常见的自组织(竞争型)神经网络还有对偶传播(Counter propagation)网络,自适应共振理论(Adaptive Resonance Theory)网络等。
生物学研究表明,在人脑的感觉通道上,神经元的组织原理是有序排列的。当外界的特定时空信息输入时,大脑皮层的特定区域兴奋,而且类似的外界信息在对应的区域是连续映像的。生物视网膜中有许多特定的细胞对特定的图形比较敏感,当视网膜中有若干个接收单元同时受特定模式刺激时,就使大脑皮层中的特定神经元开始兴奋,输入模式接近,与之对应的兴奋神经元也接近;在听觉通道上,神经元在结构排列上与频率的关系十分密切,对于某个频率,特定的神经元具有最大的响应,位置相邻的神经元具有相近的频率特征,而远离的神经元具有的频率特征差别也较大。大脑皮层中神经元的这种响应特点不是先天安排好的,而是通过后天的学习自组织形成的[2]。(注:我认为其中很大一部分是由无监督学习自发形成的)
在生物神经系统中,存在着一种侧抑制现象,即一个神经细胞兴奋以后,会对周围其他神经细胞产生抑制作用。这种抑制作用会使神经细胞之间出现竞争,其结果是某些获胜,而另一些则失败。表现形式是获胜神经细胞兴奋,失败神经细胞抑制。自组织(竞争型)神经网络就是模拟上述生物神经系统功能的人工神经网络[3]。
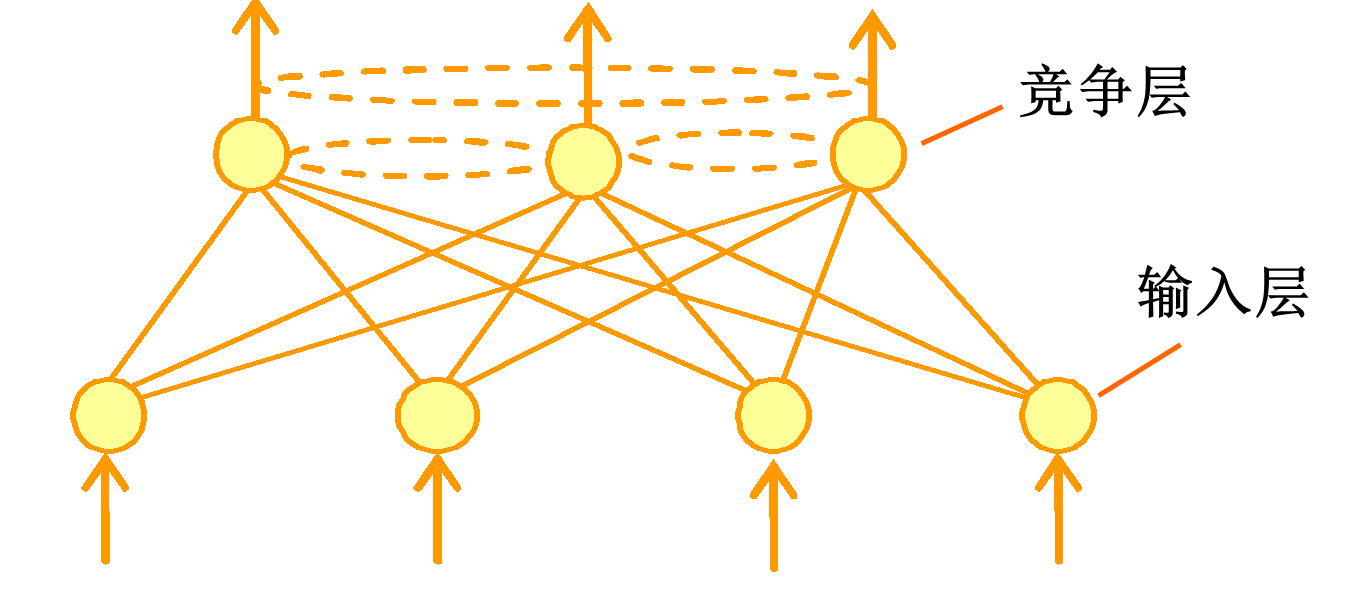
自组织(竞争型)神经网络的结构及其学习规则与其他神经网络相比有自己的特点。在网络结构上,它一般是由输入层和竞争层构成的两层网络;两层之间各神经元实现双向连接,而且网络没有隐含层。有时竞争层各神经元之间还存在横向连接(注:上面说的特点只是根据传统网络设计来说的一般情况,随着技术发展,尤其是深度学习技术的演进,我认为这种简单的自组织网络也会有所改变,比如,变得更深,或者引入time series概念)。在学习算法上,它模拟生物神经元之间的兴奋、协调与抑制、竞争作用的信息处理的动力学原理来指导网络的学习与工作,而不像多层神经网络(MLP)那样是以网络的误差作为算法的准则。竞争型神经网络构成的基本思想是网络的竞争层各神经元竞争对输入模式响应的机会,最后仅有一个神经元成为竞争的胜者。这一获胜神经元则表示对输入模式的分类[3]。因此,很容易把这样的结果和聚类联系在一起。
2、竞争学习的概念与原理
一种自组织神经网络的典型结构:如下图,由输入层和竞争层组成。主要用于完成的任务基本还是“分类”和“聚类”,前者有监督,后者无监督。聚类的时候也可以看成将目标样本分类,只是是没有任何先验知识的,目的是将相似的样本聚合在一起,而不相似的样本分离。
说到这里,一般的资料都会介绍一下欧式距离和余弦相似度,我也会讲一下基本的概念,更多距离计算方法可以参考我前面转载介绍的《距离计算方法总结》,以及《机器学习距离公式总结》,尤其是后一篇,写的不错:)
最常见的距离(相似度)计算方法就是欧氏距离和余弦相似度了,示意图如下,我就不多讲了。
很容易证明,当图中X与Xi都是模为1的单位向量时(其实不一定要1,只要是常数就行),欧氏距离等价于余弦相似度(距离最小相似度越大),而余弦相似度退化为向量内积。
竞争学习规则——Winner-Take-All
网络的输出神经元之间相互竞争以求被激活,结果在每一时刻只有一个输出神经元被激活。这个被激活的神经元称为竞争获胜神经元,而其它神经元的状态被抑制,故称为Winner Take All。
那么如何寻找获胜神经元?首先,对网络当前输入模式向量X和竞争层中各神经元对应的权重向量Wj(对应j神经元)全部进行归一化,使得X和Wj模为1;当网络得到一个输入模式向量X时,竞争层的所有神经元对应的权重向量均与其进行相似性比较,并将最相似的权重向量判为竞争获胜神经元。前面刚说过,归一化后,相似度最大就是内积最大:
因此,总结来说,竞争学习的步骤是:
(1)向量归一化
(2)寻找获胜神经元
(3)网络输出与权值调整
步骤(3)完成后回到步骤1继续训练,直到学习率衰减到0。学习率处于(0,1],一般随着学习的进展而减小,即调整的程度越来越小,神经元(权重)趋于聚类中心。
1、SOM背景
1981年芬兰Helsink大学的T.Kohonen教授提出一种自组织特征映射网,简称SOM网,又称Kohonen网。Kohonen认为:一个神经网络接受外界输入模式时,将会分为不同的对应区域,各区域对输入模式具有不同的响应特征,而且这个过程是自动完成的。自组织特征映射正是根据这一看法提出来的,其特点与人脑的自组织特性相类似。
2、SOM典型结构
典型SOM网共有两层,输入层模拟感知外界输入信息的视网膜,输出层模拟做出响应的大脑皮层。(讲之前再提醒一句,这里介绍的只是经典形式,但是希望读者和我自己不要被现有形式束缚了思维,当然初学者,包括我自己,先从基本形式开始理解吧)。 下图是1维和2维的两个SOM网络示意图。
SOM网的权值调整域
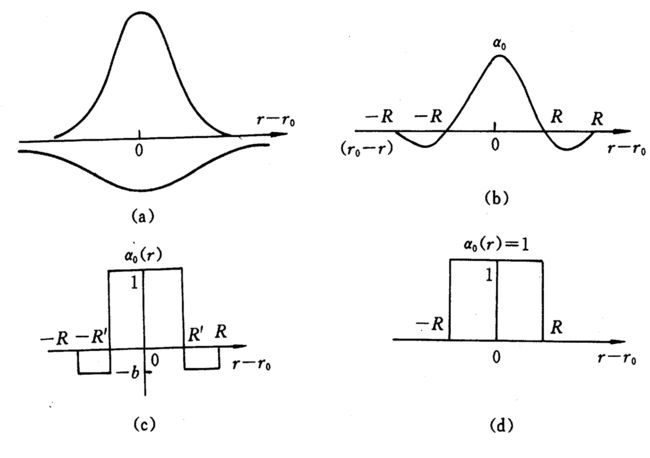
和上一节介绍的WTA策略不同,SOM网的获胜神经元对其邻近神经元的影响是由近及远,由兴奋逐渐转变为抑制,因此其学习算法中不仅获胜神经元本身要调整权向量,它周围的神经元在其影响下也要程度不同地调整权向量。这种调整可用三种函数表示,下图的bcd。
Kohonen算法:基本思想是获胜神经元对其邻近神经元的影响是由近及远,对附近神经元产生兴奋影响逐渐变为抑制。在SOM中,不仅获胜神经元要训练调整权值,它周围的神经元也要不同程度调整权向量。常见的调整方式有如下几种[2]:
- 墨西哥草帽函数:获胜节点有最大的权值调整量,临近的节点有稍小的调整量,离获胜节点距离越大,权值调整量越小,直到某一距离0d时,权值调整量为零;当距离再远一些时,权值调整量稍负,更远又回到零。如(b)所示
- 大礼帽函数:它是墨西哥草帽函数的一种简化,如(c)所示。
- 厨师帽函数:它是大礼帽函数的一种简化,如(d)所示。
以获胜神经元为中心设定一个邻域半径R,该半径圈定的范围称为优胜邻域。在SOM网学习算法中,优
胜邻域内的所有神经元均按其离开获胜神经元的距离远近不同程度地调整权值。 优胜邻域开始定得很大,但其大小随着训练次数的增加不断收缩,最终收缩到半径为零。
3、SOM Kohonen 学习算法
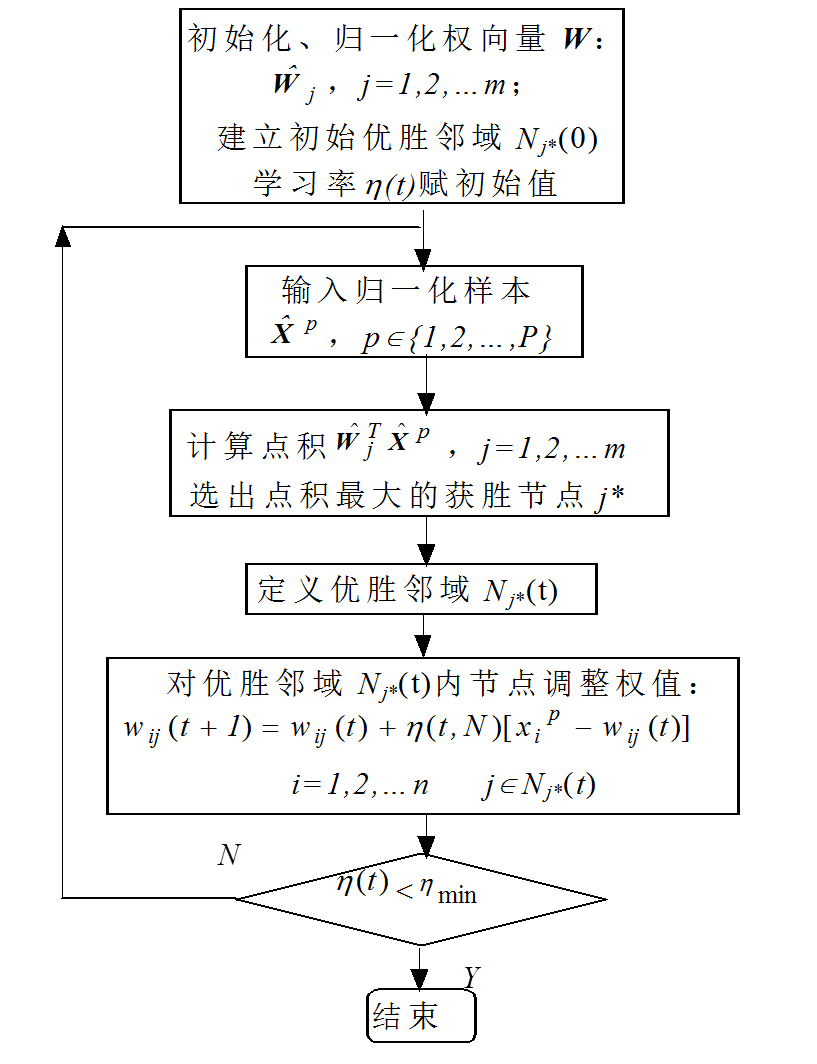
算法总结如下:
Kohonen学习算法
- 初始化,对竞争层(也是输出层)各神经元权重赋小随机数初值,并进行归一化处理,得到;建立初始优胜领域;学习率初始化;
- 对输入数据进行归一化处理,得到,总共有P个数据;
- 寻找获胜神经元:从与所有的内积中找到最大;
- 定义优胜邻域以为中心确定时刻的权值调整域,一般初始邻域较大,训练时随训练时间逐渐收缩;
调整权重,对优胜邻域内的所有神经元调整权重:
其中是一个神经元所有输入边的序标。式中,是训练时间和邻域内第j个神经元与获胜神经元之间的拓扑距离N的函数,该函数一般有如下规律: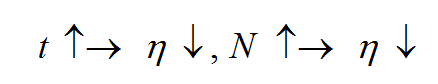
结束检查,查看学习率是否减小到0,或者以小于阈值。
第(5)点的规律是说,随着时间(离散的训练迭代次数)变长,学习率逐渐降低;随着拓扑距离的增大,学习率降低。学习率函数的形式一般可以写成这样:,其中可采用t的单调下降函数也称退火函数,比如下面这些形式都符合要求: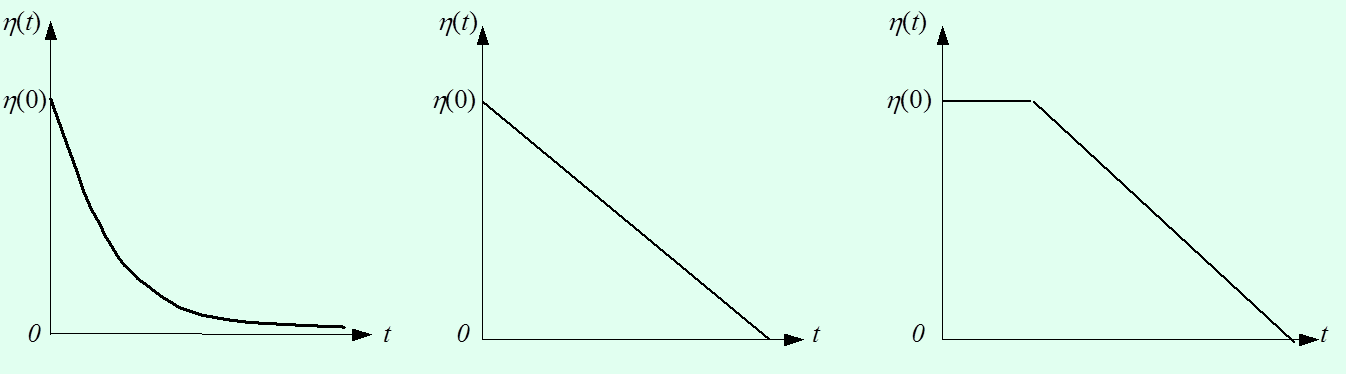
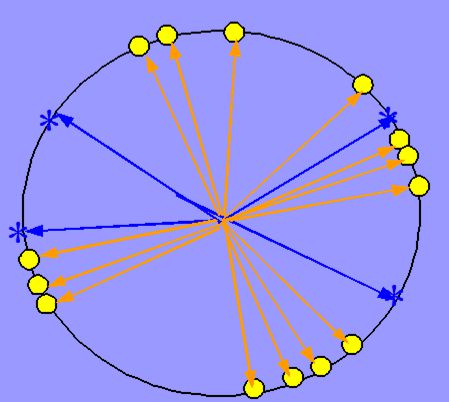
第(4)点中,j*的领域是随时间逐渐收缩的,比如说下图,其中8个邻点称为Moore neighborhoods,6个邻点的称为hexagonal grid。随着t的增大,邻域逐渐缩小。 
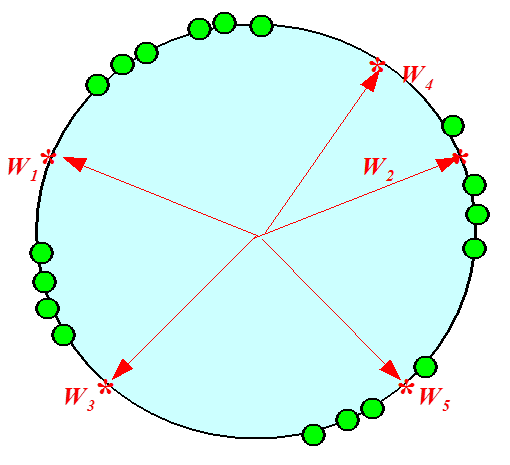
本篇最后看一个SOM工作原理示意图,首先给定训练数据(绿点)和神经元权重初始值(红花)
Test阶段,给定数据点(黄点),基于WTA策略,用内积直接算出和哪个神经元最相似就是分到哪个类。 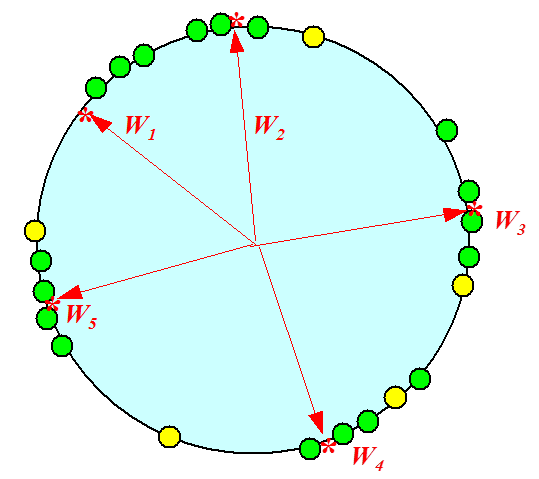
算法流程总结
第三部分
SOM设计细节
输出层设计
输出层神经元数量设定和训练集样本的类别数相关,但是实际中我们往往不能清除地知道有多少类。如果神经元节点数少于类别数,则不足以区分全部模式,训练的结果势必将相近的模式类合并为一类;相反,如果神经元节点数多于类别数,则有可能分的过细,或者是出现“死节点”,即在训练过程中,某个节点从未获胜过且远离其他获胜节点,因此它们的权值从未得到过更新。
不过一般来说,如果对类别数没有确定知识,宁可先设定较多的节点数,以便较好的映射样本的拓扑结构,如果分类过细再酌情减少输出节点。“死节点”问题一般可通过重新初始化权值得到解决。
输出层节点排列的设计
输出层的节点排列成哪种形式取决于实际应用的需要,排列形式应尽量直观反映出实际问题的物理意义。例如,对于旅行路径类的问题,二维平面比较直观;对于一般的分类问题,一个输出节点节能代表一个模式类,用一维线阵意义明确结构简单。
权值初始化问题
基本原则是尽量使权值的初始位置与输入样本的大概分布区域充分重合,不要出现大量的初始“死节点”。
- 一种简单易行的方法是从训练集中随机抽取m个输入样本作为初始权值
- 另一种可行的办法是先计算出全体样本的中心向量,在该中心向量基础上迭加小随机数作为权向量初始值,也可将权向量的初始位置确定在样本群中(找离中心近的点)。
优胜邻域的设计
优胜领域设计原则是使领域不断缩小,这样输出平面上相邻神经元对应的权向量之间既有区别又有相当的相似性,从而保证当获胜节点对某一类模式产生最大响应时,其领域节点也能产生较大响应。领域的形状可以是正方形、六边形或者菱形。优势领域的大小用领域的半径表示,的设计目前没有一般化的数学方法,通常凭借经验来选择。下面是两种典型形式:
为于输出层节点数有关的正常数, 为大于1的常数,T为预先选定的最大训练次数。
学习率的设计
在训练开始时,学习率可以选取较大的值,之后以较快的速度下降,这样有利于很快捕捉到输入向量的大致结构,然后学习率在较小的值上缓降至0值,这样可以精细地调整权值使之符合输入空间的样本分布结构。在上一篇中,我们提到最终的学习率是由学习率*优胜领域的影响,也有一些资料是把两者分开的,学习率就是一个递减的函数(学习率可以参考上面优胜邻域半径的设定形式,可选形式类似),而优胜邻域也是t的递减函数,只不过我们队优胜邻域内的点进行更新罢了。
SOM功能分析
1、保序映射——将输入空间的样本模式类有序地映射在输出层上。
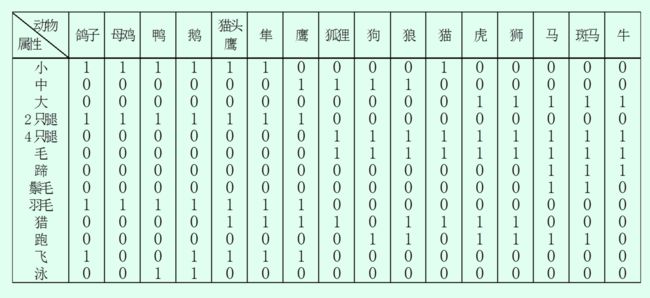
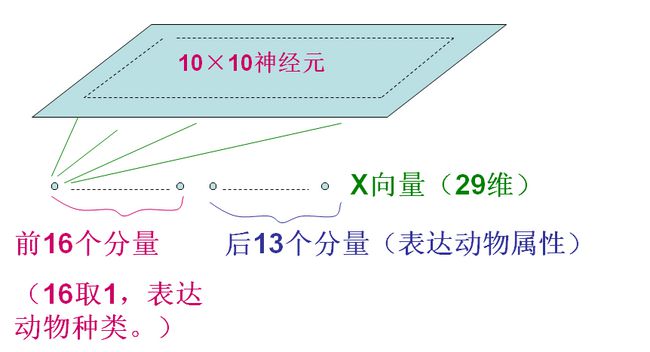
1989年Kohonen给出一个SOM网的著名应用实例,即把不同的动物按其属性映射到二维输出平面上,使属性相似的动物在SOM网输出平面上的位置也相近。训练集选了16种动物,每种动物用一个29维向量来表示。前16个分量构成符号向量(不同的动物进行16取1编码),后13个分量构成属性向量,描述动物的13种属性的有或无(用1或0表示)。
SOM网输出平面上有10×10个神经元,16个动物模式轮番输入训练,最后输出平面呈现16种动物属性特征映射,属性相似的挨在一起,实现了特征的有序分布。(实现这个图只需要判断每个神经元的模式和哪个样本最近)
2、数据压缩
将高维空间的样本在保持拓扑结构不变的条件下投影到低维的空间,在这方面SOM网具有明显的优势。无论输入样本空间是多少维,其模式都可以在SOM网输出层的某个区域得到相应。SOM网经过训练以后,在高维空间输入相近的样本,其输出相应的位置也相近。
3、特征提取
从高维空间样本向低维空间的映射,SOM网的输出层相当于低维特征空间。
另外,[2]还提到了字符排序,复合材料损伤监测等等有趣的应用,有兴趣的可以看一下。这里就不展开了。
SOM提出的比较早,算法的思想启发于人脑,主要用于无监督学习,我个人认为是很有发展空间的一类模型;另外,比较早的还有一类网络叫做hopfiled神经网络,后面有时间再写一下。好,本篇就到这里,谢谢!