建模知识2: ROC、AUC、K-S曲线
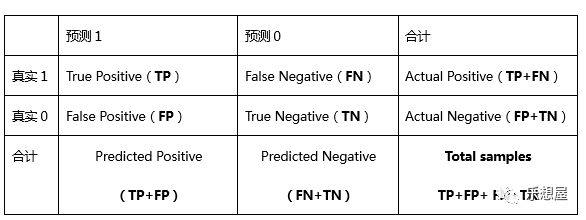
1、混淆矩阵(confusion matrix)
一个二分问题,即将实例分成正类(positive)或负类(negative)。对一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被预测成正类,即为真正类(True positive),如果实例是负类被预测成正类,称之为假正类(False positive)。相应地,如果实例是负类被预测成负类,称之为真负类(True negative),正类被预测成负类则为假负类(false negative)。
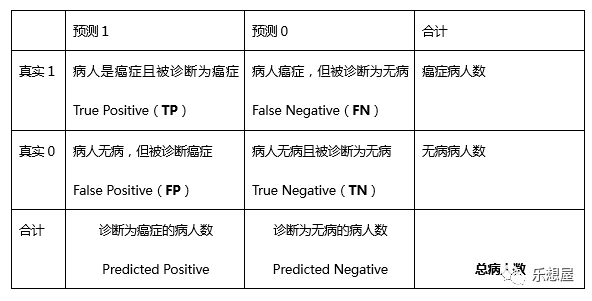
以癌症的诊断为例,1代表癌症,0代表无病。
有以下指标:
(1) TPR(True Postive Rate)真正类率:正类判断成正类,也称命中率,即所有真实的“1”中,有多少被成功选出;
(2) TNR(True Negative Rate)真负类率:负类判断成负类。Specificity(特异性)
(3) FPR(False Postive Rate)负正类率:负类判断成正类,即所有真实的“0”中,有多少被模型误判为1了。也称误诊率=1-Specificity。
2、ROC(Receiver Operating Characteristic),受试者工作特征曲线
ROC曲线最早是运用在军事上,后来逐渐运用到医学领域。相传在第二次世界大战期间,雷达兵的任务之一就是死死地盯住雷达显示器,观察是否有敌机来袭。理论上讲,只要有敌机来袭,雷达屏幕上就会出现相应的信号,但是实际上,有时如果有飞鸟出现在雷达扫描区域时,雷达屏幕上有时也会出现信号。这种情况令雷达兵烦恼不已:如果过于谨慎,凡是有信号就确定为敌机来袭,显然会增加误报风险;如果过于大胆,凡是信号都认为飞鸟,又会增加漏报的风险。每个雷达兵都竭尽所能地研究飞鸟信号和飞机信号之间的区别,以便增加预报的准确性。但问题在于,每个雷达兵都有自己的判别标准,有的雷达兵比较谨慎,容易出现误报;有的雷达兵则比较胆大,容易出现漏报。
为了研究每个雷达兵预报的准确性,雷达兵的管理者汇总了所有雷达兵的预报特点,特别是他们漏报和误报的概率,并将这些概率画到一个二维坐标里面。这个二维坐标的纵坐标为敏感性,即在所有敌机来袭的事件中,每个雷达兵准确预报的概率。而横坐标则为误诊率(1-特异性),表示了在所有非敌机来袭信号中,雷达兵预报错误的概率。由于每个雷达兵的预报标准不同,且得到的敏感性和特异性的组合也不同。将这些雷达兵的预报性能进行汇总后,雷达兵管理员发现他们刚好在一条曲线上,这条曲线就是我们经常在医学杂志上看见的ROC曲线。
横轴:负正类率(false postive rate FPR),FPR越小,误判率越低,预测正类中实际负类越小。
纵轴:真正类率(true postive rate TPR),TPR越大,命中率越高,预测正类中实际正类越多
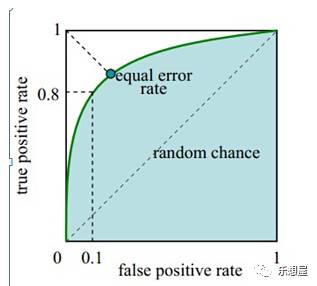
ROC曲线图中的四个点和一条线。
第一个点,(0,1),即x(FPR)=0,y(TPR)=1,这意味着FN(false negative)=0,并且FP(false positive)=0。最完美的诊断,它将所有的样本都正确分类。
第二个点,(1,0),即FPR=1,TPR=0,最糟糕的分类器,因为它成功避开了所有的正确答案。
第三个点,(0,0),即FPR=TPR=0,即FP(false positive)=TP(true positive)=0,所有样本均被预测为负样本(negative)。
第四个点(1,1),所有的样本均被预测为正样本。
最理想的模型,当然是TPR尽量高而FPR尽量低,然而任何模型在提高正确预测概率的同时,也会难以避免地增加误判率。
正确选择临界点(cutoff):
1) TPR越高,漏诊病例越少,而FPR越低,误诊率越少;
2) 在ROC曲线上,想找到一个界值,那就让两个值都取得最好的效果,那我们就往图的左上角寻找,此时越偏离45度对角线
3) 最靠近左上角的那一点为最佳临界点,点上的值即为最佳临界值,因为,此点上敏感度与特异度都较高,假阳性与假阴性也最少。
4) 即约登指数取得最大值的界值。
约登指数=敏感度+特异度-1
ROC曲线作用:
-
能很容易地查出任意界限值时的对疾病的识别能力
选择最佳的诊断界限值,权衡漏诊与误诊的影响
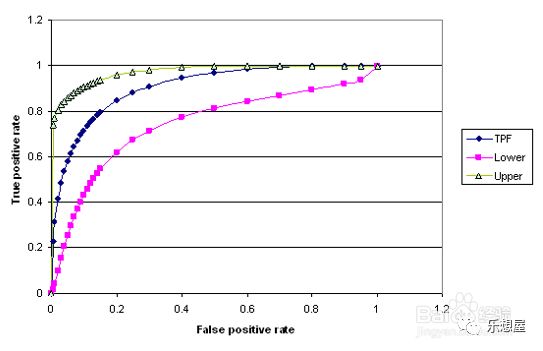
两种或两种以上不同诊断试验对疾病识别能力的比较。在对同一种疾病的两种或两种以上诊断方法进行比较时,可将各试验的ROC曲线绘制到同一坐标中,以直观地鉴别优劣,靠近左上角的ROC曲线所代表的受试者工作最准确。亦可通过分别计算各个试验的ROC曲线下的面积(AUC)进行比较,哪一种试验的AUC最大,则哪一种试验的诊断价值最佳。
把各试验的ROC曲线绘制在同一坐标中,可以直观地比较哪种诊断更有价值,如下图所示:显然绿色代表的诊断价值优于蓝色诊断,红色诊断最弱。
3、AUC(area under the ROC curve)
即ROC曲线下面积,AUC越大越好,提示该试验的诊断价值越高,模型效果越好。
1) AUC≈1.0:最理想的检查指标
2) AUC在0.7-0.9之间:试验准确性高
3) AUC=0.5:试验无诊断价值
一般来说,AUC达到0.9以上才认为是一个准确性很高的诊断试验,此时的cutoff才有实际意义。
4、K-S曲线,Kolmogorov-Smirnov Test
K-S曲线与ROC曲线异曲同工。同样是用FPR、TPR为值绘图。横坐标是阈值,纵坐标分别为TPR、FPR,绘制两条折线图。
ks值计算,ks=max(TPR-FPR),即两条曲线之间最大的间隔距离,也即好客户和坏客户的累积概率差的最大值。当ks为最大值时,同时也是ROC曲线上auc最大的值。
k-s曲线的最大值为k-s统计量。ks统计量的经验标准:
小于20:模型无鉴别能力
20-40:模型勉强接受
41-50:模型具有区别能力
51-60:模型有很好的区别能力
61-75:有非常好的区别能力
大于75:此模型异常,可能有问题
5、计算案例及曲线绘制
案例1:
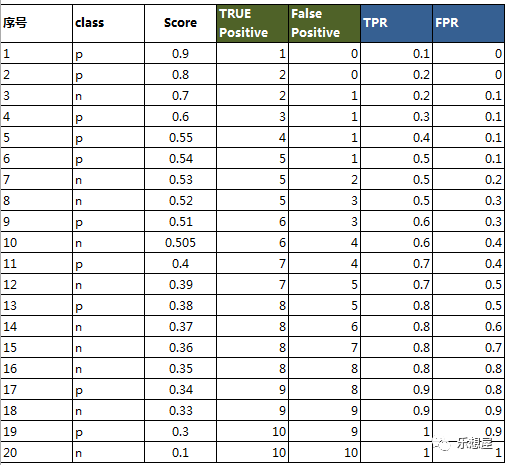
假设有20个样本,Class是样本真正的标签(p表示正样本,n表示负样本),Score表示样本被判定为正样本的概率或评分值。样本中共有正样本总数p=10个,负样本总数n=10个。
计算逻辑
1)首先按Score从高到低排列。
2)依次将Score值作为threshold(阈值),分别计算TPR、FPR。
当样本对应的score大于或等于这个threshold时,系统会把此样本预测为正样本,再与实际值class比较,就可以得出每个threshold实际正预测正的数量,以及实际负预测正的数量。TPR=TP/正样本总数(10),FPR=FP/负样本总数(10),即可得到每个threshold的TPR、FPR。
如score=0.7时,序列1-3均会被判定为正样本,因只有序号1、2为正样本,因此TRUE Positive=2,False Positive=1。TPR=2/10=0.2,FPR=1/10
如score=0.51时,序列1-9均会被判定为正样本,因只有序号1、2、4、5、9为正样本,因此TRUE Positive=5,False Positive=4。TPR=4/10=0.2,FPR=4/10。
依次类推,计算其他的threshold阈值,就可以得到20组FPR和TPR的值
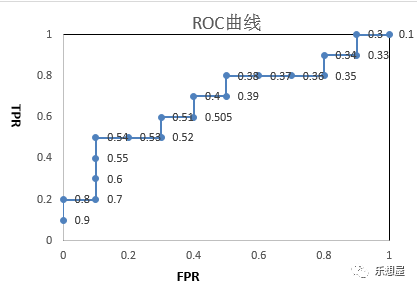
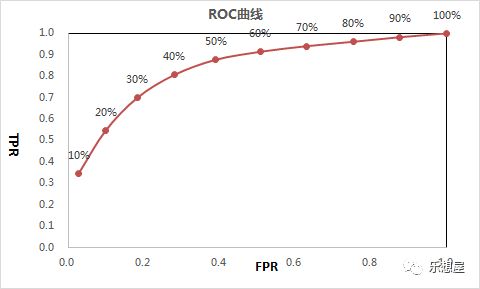
3)以FPR为横轴,TPR为纵轴,绘制散点图,即得ROC曲线
标签为阈值score
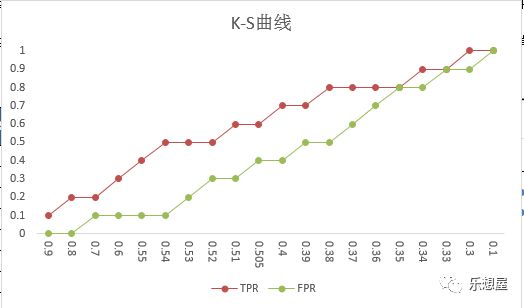
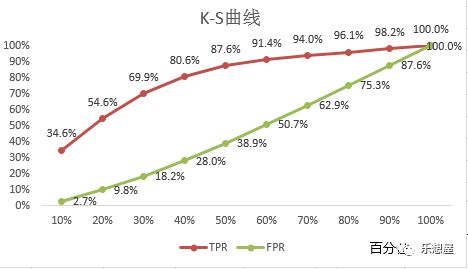
4)绘制K-S曲线
以score为横坐标,以TPR、FPR为纵坐标,绘制两条折线图
案例2:
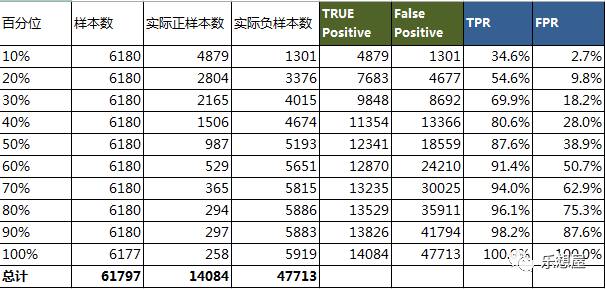
下表为逻辑回归得到的结果,样本数按预测概率(score)从大到小排列,并将样本十等分,每个部分含相同数量的样本。总样本数61797,样本中的正样本总数14084,负样本总数47713。
计算逻辑:
1)依次将Percentile作为阈值threshold,计算对应的TPR、FPR。
如:百分位10%作为阈值,则6180个样本均会被预测成正样本,其中TRUE Positive=4879,而1301则为错判为正样本,即False Positive=1301,TPR=4879/14084=34.6%,FPR=1301/47713=2.7%。
如:百分位30%作为阈值,则6180*3=18540个样本会被预测成正样本,其中TRUE Positive为9848(4879+2804+2165),False Positive为8692(1301+3376+4015),TPR=9848/14084=69.9%,FPR=8692/47713=18.2%。
依次类推,计算出10组值的TPR、FPR,并做散点图,如下,标签为阈值
2)以百分位为阈值,TPR、FPR绘制折线图
5、ROC上机实现
步骤1:导入模块
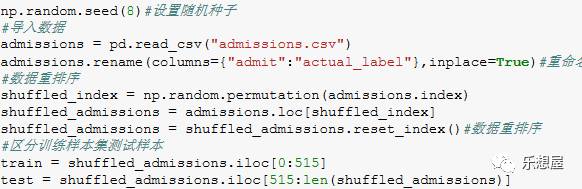
步骤2:导入数据并处理数据
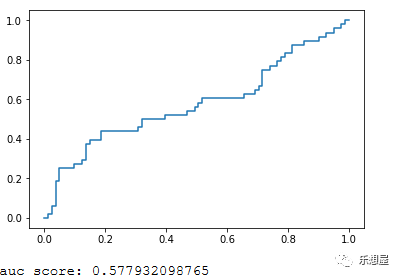
步骤3:建模并预测概率及auc
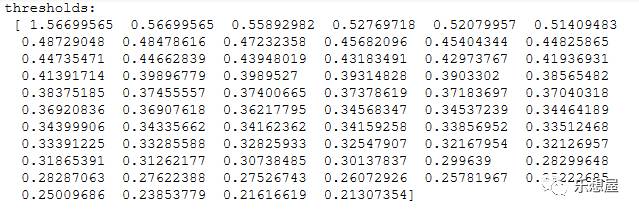
步骤4:打印结果
结果:
附:数据样本下载地址