FM，FFM,DeepFM

FM(Factorization Machines)因子分解机
主要适用的场景就是高维稀疏特征环境下，在确定输入后，它也近似于支持向量机和多项式回归。
其主要想法是，遍历所有特征，进行特征的组合，如下图，一阶特征是6个，二阶特征就有15个。

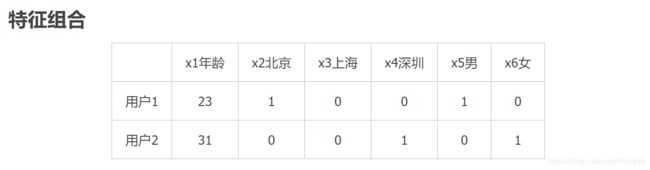
我们用如下的公式进行计算，但考虑到两个问题，一个是如上图所示，类别特征进行one-hot后会变的特征空间变大样本就变得稀疏，其次当特征组合后，新特征的样本量会变的更稀疏的问题。

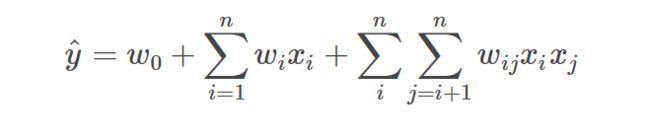
利用上式求解，使用梯度下降，由于样本量的稀疏，参数很难收敛。其次，当d=2时，由于引入特征组合也就会增添n(n-1)/2个参数w。
FM通过对w进行分解，一是可以减少模型参数，二是可以挖掘特征组合之间的相关性（个人理解）

这时参数变成了nk个，

进一步化简：

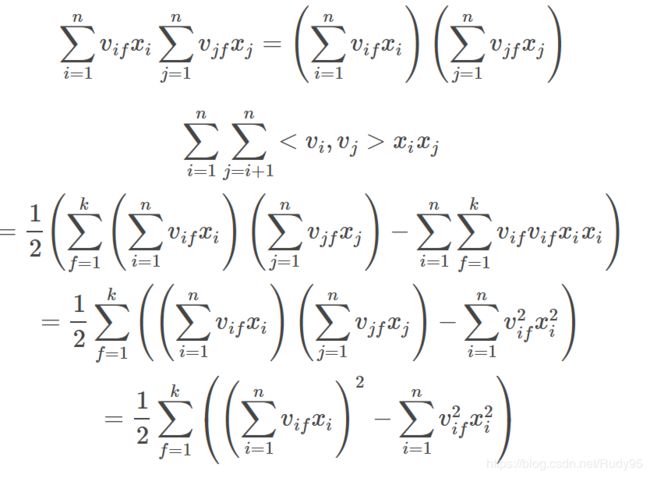
计算复杂度变成了O(nk)

FM的优点：

1. 可以在非常稀疏的数据中进行合理的参数估计
2. FM模型的时间复杂度是线性的
3. FM是一个通用模型，它可以用于任何特征为实值的情况

python实现代码：

import numpy as np
np.random.seed(0)
import random


def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))


def sigmoid_prime(z):
    """
    sigmoid函数对z求一阶偏导
    :param z:
    :return:
    """
    return sigmoid(z) * (1 - sigmoid(z))


class QuadraticCost(object):
    @staticmethod
    def fn(a, y):
        """
        平方误差损失函数
        :param a: 预测值
        :param y: 真实值
        :return:
        """
        return 0.5 * np.linalg.norm(a - y) ** 2

    @staticmethod
    def delta(z, a, y):
        """
        损失函数对z求偏导
        :param z: x的线性函数
        :param a:
        :param y:
        :return:
        """
        return (a - y) * sigmoid_prime(z)


class FM(object):
    def __init__(self, train, valid, k, eta, maxecho, r2, cost=QuadraticCost):
        """
        构造函数
        :param train: 训练数据
        :param valid: 验证数据
        :param k: 矩阵V的第2维
        :param eta: 固定学习率
        :param maxecho: 最多迭代次数
        :param r2: R2小于该值后可停止迭代
        :param cost: 损失函数
        """
        self.train_x = train[:, :-1]
        self.train_y = train[:, -1:]
        self.valid_x = valid[:, :-1]
        self.valid_y = valid[:, -1:]
        self.var_y = np.var(self.valid_y)  # y的方差，在每轮迭代后计算R2时要用到
        self.k = int(k)
        self.eta = float(eta)
        self.maxecho = maxecho
        self.r2 = r2
        self.cost = cost
        # 用正态分布随机初始化参数W和V
        self.w0 = np.random.randn()
        self.w = np.random.randn(1, self.train_x.shape[1])
        self.v = np.random.randn(self.train_x.shape[1], self.k)

    def shuffle_data(self):
        """
        每轮训练之前都随机打乱样本顺序
        :return:
        """
        ids = list(range(len(self.train_x)))
        random.shuffle(ids)
        self.train_x = self.train_x[ids]
        self.train_y = self.train_y[ids]

    def predict(self, x):
        """
        根据x求y
        :param x:
        :return:
        """
        z = self.w0 + np.dot(self.w, x.T).T + np.longlong(
            np.sum((np.dot(x, self.v) ** 2 - np.dot(x ** 2, self.v ** 2)),
                   axis=1).reshape(len(x), 1)) / 2.0

        return z, sigmoid(z)

    def evaluate(self):
        """
        在验证集上计算R2
        :return:
        """
        _, y_hat = self.predict(self.valid_x)
        mse = np.sum((y_hat - self.valid_y) ** 2) / len(self.valid_y)
        r2 = 1.0 - mse / self.var_y
        print ("r2={}".format(r2))
        return r2

    def update_mini_batch(self, x, y, eta):
        """
        平方误差作为损失函数，梯度下降法更新参数
        :param x:
        :param y:
        :param eta: 学习率
        :return:
        """
        batch = len(x)
        step = eta / batch
        z, y_hat = self.predict(x)
        y_diff = self.cost.delta(z, y_hat, y)
        self.w0 -= step * np.sum(y_diff)
        self.w -= step * np.dot(y_diff.T, x)
        delta_v = np.zeros(self.v.shape)
        for i in range(batch):
            xi = x[i:i + 1, :]  # mini_batch中的第i个样本。为保持shape不变，注意这里不能用x[i]
            delta_v += (np.outer(xi, np.dot(xi, self.v)) - xi.T ** 2 * self.v) * (y_diff[i])
        self.v -= step * delta_v

    def train(self, mini_batch=100):
        """
        采用批量梯度下降法训练模型
        :param mini_batch:
        :return:
        """
        for itr in range(self.maxecho):
            print ("iteration={}".format(itr))
            self.shuffle_data()
            n = len(self.train_x)
            for b in range(0, n, mini_batch):
                x = self.train_x[b:b + mini_batch]
                y = self.train_y[b:b + mini_batch]
                learn_rate = np.exp(-itr) * self.eta  # 学习率指数递减
                self.update_mini_batch(x, y, learn_rate)

            if self.evaluate() > self.r2:
                break


def fake_data(sample, dim, k):
    """
    构造假数据
    :param sample:
    :param dim:
    :param k:
    :return:
    """
    w0 = np.random.randn()
    w = np.random.randn(1, dim)
    v = np.random.randn(dim, int(k))
    x = np.random.randn(sample, dim)
    z = w0 + np.dot(w, x.T).T + np.longlong(
        np.sum((np.dot(x, v) ** 2 - np.dot(x ** 2, v ** 2)),
               axis=1).reshape(len(x), 1)) / 2.0
    y = sigmoid(z)
    data = np.concatenate((x, y), axis=1)
    return z, data


if __name__ == "__main__":
    dim = 9  # 特征的维度
    k = dim / 3
    sample = 100
    z, data = fake_data(sample, dim, k)

    train_size = int(0.7 * sample)
    valid_size = int(0.2 * sample)
    train = data[:train_size]  # 训练集
    valid = data[train_size:train_size + valid_size]  # 验证集
    test = data[train_size + valid_size:]  # 测试集
    test_z = z[train_size + valid_size:]

    eta = 0.01  # 初始学习率
    maxecho = 200
    r2 = 0.9  # 拟合系数r2的最小值
    fm = FM(train, valid, k, eta, maxecho, r2)
    fm.train(mini_batch=50)

    test_x = test[:, :-1]
    test_y = test[:, -1:]
    print ('z=', test_z)
    print ("y=", test_y)
    z_hat, y_hat = fm.predict(test_x)
    print ("z_hat=", z_hat)
    print ("y_hat=", y_hat)

FM的优点和缺点：
优点：解决稀疏数据下的特征组合问题，具有线性复杂度，一般的线性模型没有考虑特征间的关联，
训练集中不存在的特征组合，通过FM的隐向量也能得到该组合的权重，还有论文中提到，在某些特殊的输入下，相当于多项式核SVM。
缺点：针对高阶的特征组合，计算复杂度很大；对于类别特征类别特别多，依旧会产生特征稀疏的问题；每个特征都只有一个特征向量，与不同类型特征组合时，使用的是同一种特征，这从一方面来说是不合理的。比如，年龄城市，年龄性别，这两者组合年龄的特征向量都是不变的。考虑到这个因素，推出了FFM.

FFM：

FFM主要是改进了FM中的每个特征的隐向量，针对FM中一个特征只有一个隐向量，组合不合理，FFM将每个特征都构建（f-1）个向量，f是field的个数，FFM把相同性质的特征归于同一个field，同一个categorical特征经过One-Hot编码生成的数值特征都可以放到同一个field，包括用户性别、职业、品类偏好等。
FFM的优点：
主要是引入场的概念，进一步缩小了特征空间，一个是使得隐向量的学习更加合理，还有就是解决了one-hot类别特别多的问题。
缺点：依旧是无法解决高阶特征组合计算问题

DeepFM

先套用网上的图，deepFM是结合了FM和DNN两者实现一种模型。FM模型考虑计算复杂度等问题，很多时候最多使用到二阶特征组合，而更高阶则没有办法了，而DNN恰巧弥补了这一点，通过DNN提取高阶特征，最终将FM和DNN的结果进行组合。

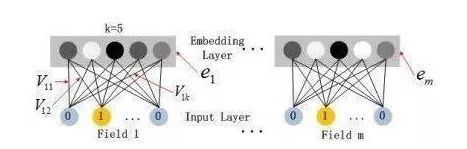
首先第一层是一个嵌入层，FM和DNN共享嵌入层的输入。假设特征有m个，field为F,嵌入层嵌入维度为K,则经过嵌入层得到的,嵌入层的权重实际就是FM中的权重，得到的输出是每条数据的表示。
嵌入层维度：m*K
输出的维度是:F*K

			# model
            self.embeddings = tf.nn.embedding_lookup(self.weights["feature_embeddings"],
                                                             self.feat_index)  # None * F * K，得到每条数据，场以及场对应的嵌入
            feat_value = tf.reshape(self.feat_value, shape=[-1, self.field_size, 1])
            self.embeddings = tf.multiply(self.embeddings, feat_value)##得到嵌入层的表示，再乘以特征值，这是为了二次项准备

FM部分：（每条数据虽然有f个特征，但是很多特征因为都是同一个场，一个场里都只有一个值，所以真正有值的特征就是各个场的个数）
输入：F*K
根据公式计算一阶特征

# ---------- first order term ----------一次项
            self.y_first_order = tf.nn.embedding_lookup(self.weights["feature_bias"], self.feat_index) # None * F * 1，feature_bias是一次项权重系数
            self.y_first_order = tf.reduce_sum(tf.multiply(self.y_first_order, feat_value), 2)  # None * F，一次项里，场权重乘以特征
            self.y_first_order = tf.nn.dropout(self.y_first_order, self.dropout_keep_fm[0]) # None * F

输出维度：None*F
二阶特征

由于上述公式可以推导成：

代码中可以先计算好隐向量v和x的乘积，如下面代码所示：

            # ---------- second order term ---------------##求和再平方
            # sum_square part
            self.summed_features_emb = tf.reduce_sum(self.embeddings, 1)  # None * K
            self.summed_features_emb_square = tf.square(self.summed_features_emb)  # None * K

            # square_sum part平方再求和
            self.squared_features_emb = tf.square(self.embeddings)
            self.squared_sum_features_emb = tf.reduce_sum(self.squared_features_emb, 1)  # None * K

            # second order
            self.y_second_order = 0.5 * tf.subtract(self.summed_features_emb_square, self.squared_sum_features_emb)  # None * K
            self.y_second_order = tf.nn.dropout(self.y_second_order, self.dropout_keep_fm[1])  # None * K

最后的输出维度：None*K
DNN部分：
将嵌入层的输入F*K，reshape成None*(F*K)
经过几层全连接，得到DNN部分的输出，输出维度，None*layer[-1]
最终的组合：

DeepFM优点：
实现了二阶和高阶特征组合；
FM和DNN共享feature_embedding，减少了参数的数量；
不需要人工提取特征；

缺点：
（目前不清楚）

推荐一个很不错的链接：https://blog.csdn.net/John_xyz/article/details/78933253
参考链接：
公式求导：https://www.cnblogs.com/zhangchaoyang/articles/7897085.html
https://zhuanlan.zhihu.com/p/63267172
开源实现以及对应代码的讲解：
https://cloud.tencent.com/developer/article/1450677
https://github.com/ChenglongChen/tensorflow-DeepFM
DeepFM的改进：
https://zhuanlan.zhihu.com/p/48057256