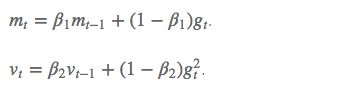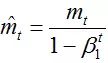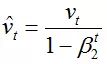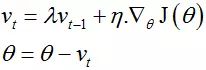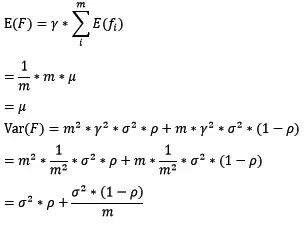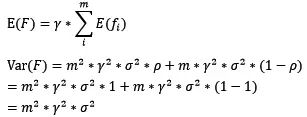算法工程师面试题整理1(待续)
面试题整理
- 1.adam的特点
- Adam:Adaptive Moment Estimation
- 补充1:Momentum
- 2.em算法
- 3.lr为什么要使用sigmoid
- 补充1:逻辑回归(logistics regression)
- 4.从方差和偏差角度比较bagging和boosting
- boosting的偏差和方差
- 补充1:偏差和方差与模型复杂度关系
- 5.svm如何实现多分类
- 一对多(one-versus-rest,简称OVR SVMs)
- 一对一(one-versus-one,简称OVO SVMs或者pairwise)
- 6.a,b为[0,1]的独立均匀分布,求E(max(a,b))的值
- 7.python中的a is b和a = b的区别
- 补充1.b=a与b=a[:]的区别
- 8.python中的生成器、迭代器的区别
- 迭代器
- 生成器
- 9.python中什么是装饰器
- 10.python中copy,deepcopy,赋值 = 的区别
- 11.tf如何读取数据
- 12.L1,L2正则化的梯度公式,区别与应用场景
- 13.线性回归和lr回归的区别
- 14.softmax梯度下降公式
- 15.模型出处后接全连接层的原因,是否有什么改进
- 16.lr的损失函数,为什么要用交叉熵
- 17.什么样的任务适合用深度学习,什么样的问题不适合
- 18.精确度和召回率
- 19.tensorflow么 底层如何实现
- 20.方差和偏置
- 21.knn与k-means的区别
- 22.1*1 卷积的作用
- 23.gdbt、xgboost、随机森林有什么区别
- 24.python 旋转二维矩阵
- 25.过拟合、欠拟合
- 26.栈和队列的区别
- 27.推导svm
- 28.为什么使用sigmoid激活函数会导致梯度消失
- 29.Adaboost和XGboost的区别
- 30.Kmeans和EM有什么关系,和GMM有什么关系?
- 31.LR为什么要离散特征
- 32.熟悉instance segmentation嘛?
1.adam的特点
Adam:Adaptive Moment Estimation
这个算法是一种计算每个参数的自适应学习率的方法。相当于 RMSprop + Momentum
除了像 Adadelta 和 RMSprop 一样存储了过去梯度的平方 vt 的指数衰减平均值 ,也像 momentum 一样保持了过去梯度 mt 的指数衰减平均值:
补充1:Momentum
动量可以加速SGD算法的收敛速度,并且降低SGD算法收敛时的震荡。
- 通过添加一个衰减因子到历史更新向量,并加上当前的更新向量。当梯度保持相同方向时,动量因子加速参数更新;而梯度方向改变时,动量因子能降低梯度的更新速度。
- 当我们将一个小球从山上滚下来时,没有阻力的话,它的动量会越来越大,但是如果遇到了阻力,速度就会变小。
- 加入的这一项,可以使得梯度方向不变的维度上速度变快,梯度方向有所改变的维度上的更新速度变慢,这样就可以加快收敛并减小震荡。
2.em算法
3.lr为什么要使用sigmoid
- 逻辑回归也被称为广义线性回归模型,它与线性回归模型的形式基本上相同,都具有 ax+b,其中a和b是待求参数,
- 其区别在于他们的因变量不同,多重线性回归直接将ax+b作为因变量,即y = ax+b,而logistic回归则通过函数S将ax+b对应到一个隐状态p,p = S(ax+b),然后根据p与1-p的大小决定因变量的值。这里的函数S就是Sigmoid函数
S ( t ) = 1 1 + e − t S(t) = \frac{1}{1 + e^{-t}} S(t)=1+e−t1
求导: S ( t ) ′ = S ( t ) ( 1 − S ( t ) ) {S(t)}'=S(t)(1-S(t)) S(t)′=S(t)(1−S(t))
将t换成ax+b,可以得到逻辑回归模型的参数形式:
p ( x ; a , b ) = 1 1 + e − ( a x + b ) … … ( 1 ) p(x; a,b) = \frac{1}{1 + e^{-(ax+b)}} ……(1) p(x;a,b)=1+e−(ax+b)1……(1)
同时,也可见 ϕ = 1 1 + e − η \phi =\frac{1}{1+e^{-\eta }} ϕ=1+e−η1就是逻辑回归中simgod函数
还有最大熵的原因:还未搞清楚,最大熵可以退出softmax形式的多分类
补充1:逻辑回归(logistics regression)
逻辑回归虽然名字叫做回归,但实际上却是一种分类学习方法
4.从方差和偏差角度比较bagging和boosting
- 模型的偏差:训练出来的模型在训练集上的准确度。
- 模型的方差: 是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。描述数据离散程度,数据波动性,会影响模型的预测结果。
首先来看方差的定义:设X为随机变量,则方差 V a r ( X ) = E [ ( X − E [ X ] ) 2 ] Var(X) = E[(X-E[X])^2] Var(X)=E[(X−E[X])2],表示X与平均值 E[X] 之间差异的平方的期望值,用于刻画X取值的散布程度。
方差有两个重要的性质,后文会用到:c为常数,则
V a r ( c X ) = E [ ( c X − E [ c X ] ) 2 ] = c 2 E [ ( X − E [ X ] ) 2 ] = c 2 V a r ( X ) Var(cX) = E[(cX - E[cX])^2] = c^2E[(X-E[X])^2] = c^2Var(X) \qquad Var(cX)=E[(cX−E[cX])2]=c2E[(X−E[X])2]=c2Var(X)
独立随机变量之和的方差等于各变量的方差之和:
V a r ( X 1 + ⋯ + X n ) = V a r ( X 1 ) + ⋯ + V a r ( X n ) Var(X_1 + \cdots + X_n) = Var(X_1) + \cdots +Var(X_n) \qquad Var(X1+⋯+Xn)=Var(X1)+⋯+Var(Xn)
- 根据上式我们可以看到,整体模型的期望近似于基模型的期望,这也就意味着整体模型的偏差和基模型的偏差近似。 因此:bagging中的基模型一定要为强模型,否则就会导致整体模型的偏差度低,即准确度低。
- 同时,整体模型的方差小于等于基模型的方差(当相关性为1时取等号)
- 随着基模型数(m)的增多,整体模型的方差减少,从而防止过拟合的能力增强,模型的准确度得到提高
boosting的偏差和方差
对于boosting来说,基模型的训练集抽样是强相关的,那么模型的相关系数近似等于1,故我们也可以针对boosting化简公式为:
- 通过观察整体方差的表达式,我们容易发现,若基模型不是弱模型,其方差相对较大,这将导致整体模型的方差很大,即无法达到防止过拟合的效果。因此,boosting框架中的基模型必须为弱模型。
- 因为基模型为弱模型,导致了每个基模型的准确度都不是很高(因为其在训练集上的准确度不高)。随着基模型数的增多,整体模型的期望值增加,更接近真实值,因此,整体模型的准确度提高。但是准确度一定会无限逼近于1吗?仍然并不一定,因为训练过程中准确度的提高的主要功臣是整体模型在训练集上的准确度提高,而随着训练的进行,整体模型的方差变大,导致防止过拟合的能力变弱,最终导致了准确度反而有所下降。
补充1:偏差和方差与模型复杂度关系
- 越复杂的模型,偏差越小,方差越大,会出现过拟合
- 参数少简单模型,会得到低方差,高偏差,会出现欠拟合
5.svm如何实现多分类
一对多(one-versus-rest,简称OVR SVMs)
训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类,这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。
举个例子:假如我有四类要划分(也就是有存在四个Label),他们是A、B、C、D。 于是我在抽取训练集的时候,分别选取四个训练集如下:
- A所对应的向量作为正集,B,C,D所对应的向量作为负集;
- B所对应的向量作为正集,A,C,D所对应的向量作为负集;
- C所对应的向量作为正集,A,B,D所对应的向量作为负集;
- D所对应的向量作为正集,A,B,C所对应的向量作为负集;
{可以概括为 自己一类为正集 其余类为负集,N个类别(N个label)有N个训练集}
使用这四个训练集分别进行训练,然后的得到四个训练结果文件。在测试的时候,把对应的测试向量分别利用这四个训练结果文件进行测试。
最后每个测试都有一个结果f1(x),f2(x),f3(x),f4(x)。
于是最终的结果便是这四个值中最大的一个作为分类结果。
评价:
优点:训练k个分类器,个数较少,其分类速度相对较快。
缺点:①每个分类器的训练都是将全部的样本作为训练样本,这样在求解二次规划问题时,训练速度会随着训练样本的数量的增加而急剧减慢;
②同时由于负类样本的数据要远远大于正类样本的数据,从而出现了样本不对称的情况,且这种情况随着训练数据的增加而趋向严重。解决不对称的问题可以引入不同的惩罚因子,对样本点来说较少的正类采用较大的惩罚因子C;
③还有就是当有新的类别加进来时,需要对所有的模型进行重新训练。
{补充:有以下两个问题:
- 一个是一个样本可能同时属于几个类
那么看一下这个样本到各个超平面的距离,哪个远判给哪个 - 另一个是一个样本可能不属于任何一个
这样这个样本属于第N+1类,这个类的数目远大于N类之和,所以会造成数据偏斜问题}
一对一(one-versus-one,简称OVO SVMs或者pairwise)
其做法是在任意两类样本之间设计一个SVM,因此k个类别的样本就要设计k(k-1)/2个SVM。
当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别。
Libsvm(一个好用的包)中的多类分类就是根据这个方法实现的
{关于libsvm的使用说明等可以参考(https://www.cnblogs.com/jingyesi/p/4237155.html)}
举个例子:
假设有四类A,B,C,D四类。在训练的时候我选择A,B; A,C; A,D; B,C; B,D;C,D所对应的向量作为训练集(4X3/2=6),然后得到六个训练结果,在测试的时候,把对应的向量分别对六个结果进行测试,然后采取投票形式,最后得到一组结果。
投票是这样的:
A=B=C=D=0;
(A,B)-classifier 如果是A win,则A=A+1;otherwise,B=B+1;
(A,C)-classifier 如果是A win,则A=A+1;otherwise, C=C+1;
…
(C,D)-classifier 如果是A win,则C=C+1;otherwise,D=D+1;
The decision is the Max(A,B,C,D)
(也就是通过看投票的分数来看分类情况)
评价:这种方法虽然好,但是当类别很多的时候,model的个数是n*(n-1)/2,代价还是相当大的。与一对多相比不会有样本不属于任何一类的情形出现,但是复杂度变大了。
6.a,b为[0,1]的独立均匀分布,求E(max(a,b))的值
7.python中的a is b和a = b的区别
- a == b , 这是一个比较运算符,用于比较两个对象的value(值)是否相同
相同则返回True 否则返回False - a is b , 这是一个同一性运算符。用于比较两个对象的物理id。
如果相同则返回True 否则返回False
补充1.b=a与b=a[:]的区别
- b=a将两者指向同一个对象
- 而b=a[:]会创建一个新的与a完全相同的对象,但是与a并不指向同一对象。
8.python中的生成器、迭代器的区别
迭代器
- 它是一个带状态的对象,他能在你调用next()方法的时候返回容器中的下一个值,任何实现了__iter__和__next__()(python2中实现next())方法的对象都是迭代器,__iter__返回迭代器自身,__next__返回容器中的下一个值,如果容器中没有更多元素了,则抛出StopIteration异常。
- 任何实现了__iter__和__next__()方法的对象都是迭代器。__iter__返回迭代器自身,__next__返回容器中的下一个值。
- 迭代器就像一个懒加载的工厂,等到有人需要的时候才给它生成值返回,没调用的时候就处于休眠状态等待下一次调用。

- 实现方式
class Fib:
def __init__(self):
self.prev = 0
self.curr = 1
def __iter__(self):
return self
def __next__(self):
value = self.curr
self.curr += self.prev
self.prev = value
return value
f = Fib()
count = 1
for n in f:
print(n)
count = count+1
if count>=10:
break
//Out:1 1 2 3 5 8 13 21 34
生成器
- 生成器算得上是Python语言中最吸引人的特性之一,生成器其实是一种特殊的迭代器,不过这种迭代器更加优雅。它不需要再像上面的类一样写__iter__()和__next__()方法了,只需要一个yiled关键字。 生成器一定是迭代器(反之不成立)
- 生成器在Python中是一个非常强大的编程结构,可以用更少地中间变量写流式代码,此外,相比其它容器对象它更能节省内存和CPU,当然它可以用更少的代码来实现相似的功能
- 方式一
//区别于列表生成式 gen = [x*x for x in range(5)]
gen = (x*x for x in range(5))
print(gen) //Out:<generator object <genexpr> at 0x00000258DC5CD8E0>
print(next(gen)) //0
print(next(gen)) //1
...
print(next(gen)) //16
print(next(gen)) //StopIteration
for n in gen:
print(n) //0 1 4 9 16
- 方式二
def fib():
prev, curr = 0, 1
while True:
yield curr
prev, curr = curr, curr + prev
f = fib()
print(f) //Out:<generator object fib at 0x00000258DC5CD150>
print(next(f)) //1
9.python中什么是装饰器
10.python中copy,deepcopy,赋值 = 的区别
- python3中,直接可以使用copy()方法,但deepcopy()还是需要导入copy模块
- 深复制,即将被复制对象完全再复制一遍作为独立的新个体单独存在。所以改变原有被复制对象不会对已经复制出来的新对象产生影响。
- = 等于赋值,并不会产生一个独立的对象单独存在,他只是将原有的数据块打上一个新标签,所以当其中一个标签被改变的时候,数据块就会发生变化,另一个标签也会随之改变。
- 浅复制要分两种情况进行讨论:
1)当浅复制的值是不可变对象(数值,字符串,元组)时和“等于赋值”的情况一样,对象的id值与浅复制原来的值相同。
2)当浅复制的值是可变对象(列表和字典)时会产生一个“不是那么独立的对象”存在。有两种情况:- 第一种情况:复制的对象中无复杂子对象,原来值的改变并不会影响浅复制的值,同时浅复制的值改变也并不会影响原来的值。原来值的id值与浅复制原来的值不同。
- 第二种情况:复制的对象中有复杂子对象(例如列表中的一个子元素是一个列表),如果不改变其中复杂子对象,浅复制的值改变并不会影响原来的值。 但是改变原来的值中的复杂子对象的值会影响浅复制的值。
11.tf如何读取数据
12.L1,L2正则化的梯度公式,区别与应用场景
https://blog.csdn.net/Trista2hong/article/details/90289451
13.线性回归和lr回归的区别
14.softmax梯度下降公式
15.模型出处后接全连接层的原因,是否有什么改进
16.lr的损失函数,为什么要用交叉熵
- 主要原因:
- 均方差对参数的偏导的结果都乘了sigmoid的导数σ′(z),而之前看图发现sigmoid导数在其变量值很大或很小时趋近于0,所以偏导数很有可能接近于0。
- 由参数更新公式: 参数=参数−学习率×损失函数对参数的偏导
- 可知,偏导很小时,参数更新速度会变得很慢,而当偏导接近于0时,参数几乎就不更新了。
- 反观交叉熵对参数的偏导就没有sigmoid导数,所以不存在这个问题。这就是选择交叉熵而不选择均方差的原因。
- 原因2:
- 计算损失,理应使用相对熵来计算概率分布的差异,然而由相对熵推导出的结果看:
- 相对熵=交叉熵−信息熵
- 由于信息熵描述的是消除 p (即真实分布) 的不确定性所需信息量的度量,所以其值应该是最小的、固定的。那么:优化减小相对熵也就是优化交叉熵,所以在机器学习中使用交叉熵就可以了
https://blog.csdn.net/huwenxing0801/article/details/82791879
17.什么样的任务适合用深度学习,什么样的问题不适合
18.精确度和召回率
19.tensorflow么 底层如何实现
20.方差和偏置
21.knn与k-means的区别
| KNN | K-Means |
|---|---|
| 目的是为了确定一个点的分类 | 目的是为了将一系列点集分成k类 |
| KNN是分类算法 | K-Means是聚类算法 |
| 监督学习,分类目标事先已知 | 非监督学习,将相似数据归到一起从而得到分类,没有外部分类 |
| 训练数据集有label,已经是完全正确的数据 | 训练数据集无label,是杂乱无章的,经过聚类后才变得有点顺序,先无序,后有序 |
| 没有明显的前期训练过程,属于memory-based learning | 有明显的前期训练过程 |
| K的含义:“k”是用来计算的相邻数据数。来了一个样本x,要给它分类,即求出它的y,就从数据集中,在x附近找离它最近的K个数据点,这K个数据点,类别c占的个数最多,就把x的label设为c | K的含义:“k”是类的数目。K是人工固定好的数字,假设数据集合可以分为K个簇,由于是依靠人工定好,需要一点先验知识 |
| K值确定后每次结果固定 | K值确定后每次结果可能不同,从 n个数据对象任意选择 k 个对象作为初始聚类中心,随机性对结果影响较大 |
| 时间复杂度:O(n) | 时间复杂度:O(nkt),t为迭代次数 |
相似点:都包含这样的过程,给定一个点,在数据集中找离它最近的点。即二者都用到了NN(Nears Neighbor)算法,一般用KD树来实现NN
22.1*1 卷积的作用
- 在大多数情况下它作用是升/降特征的维度:在Inception网络( Going Deeper with Convolutions )中用来降维,在resnet中用于降维,但mobilenet v3用于降维
- 另一种角度去理解1*1卷积,可以把它看成是一种全连接
- 加入非线性。卷积层之后经过激励层,1*1的卷积在前一层的学习表示上添加了非线性激励( non-linear activation ),提升网络的表达能力;
23.gdbt、xgboost、随机森林有什么区别
24.python 旋转二维矩阵
#zip()
a=[[1,2,3,4,5],[6,7,8,9,0],[11,12,13,14,15]]
# 利用zip()
aT=list(map(list,zip(*a)))
print(aT) # [[1, 6, 11], [2, 7, 12], [3, 8, 13], [4, 9, 14], [5, 0, 15]
25.过拟合、欠拟合
26.栈和队列的区别
27.推导svm
28.为什么使用sigmoid激活函数会导致梯度消失
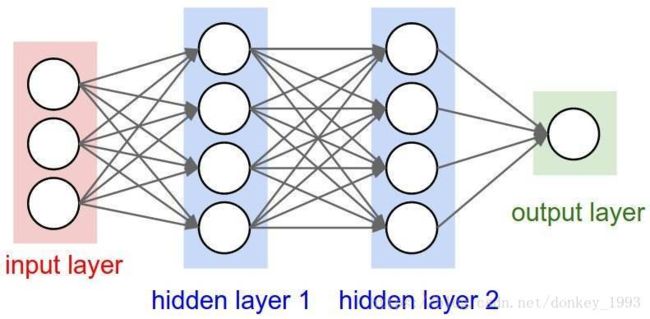
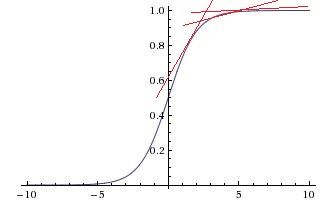
(当x取值越大,它的导数就越接近于0.这样求不同的网络层参数w对loss的贡献的时候就会出现梯度消失问题)
假设 inputer layer 和 hidden layer1 之间的参数为w1 ,layer1和layer2之间的参数为w2,layer2和output layer之间的参数为w3. 对于深度学习来说我们需要做一个求导的操作(反向传播),需要求w3,w2,w1分别对loss做的了多少贡献。w1计算对loss的贡献时需要累乘前面w2和w3的导数,w2就需要累乘w3的导数。假设我们用的是sigmoid激活函数,假设我们的取值比较大的时候w3,w2,w1的取值在sigmoid函数上面的斜率就趋近于0,这样当w3,w2, w1相乘就更加趋近于0了就出现了梯度消失的问题。
29.Adaboost和XGboost的区别
30.Kmeans和EM有什么关系,和GMM有什么关系?
31.LR为什么要离散特征
1.稀疏向量内积乘法运算速度快,计算结果方便存储,容易scalable(扩展)。
2.离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰。
3.逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合。
4.离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力。
5.特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问;
大概的理解:
1)计算简单
2)简化模型
3)增强模型的泛化能力,不易受噪声的影响