大数阶乘算法实现及优化
题目:求N! Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K
(Java/Others) Total Submission(s): 63958 Accepted Submission(s):
18171
Problem Description:
Given an integer N(0 ≤ N ≤ 10000), your task is to calculate N! Input One N in one line, process to the end of file. Output For each N, output N! in one line.
Sample Input
1
2
3
Sample Output
1
2
6解决思路:
由于题目要求计算的范围为10000以内,为了符合题目要求我们先分析10000!有多大,根据公式N!的位数=[lg(1)+lg(2)+…..log(N)]+1([]表示向上取整)可知,10000!大概37000多位,所以可以用40000个元素的int数组res保存.。为了方便起见,res[0]保存结果的个位,res[1]保存百位………(为什么要逆序呢,这样方便进位)。
代码实现:
//============================================================================
// Author : Up_Junior
// Version : Vs2012
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//============================================================================
#include //clock_t使用导入头文件。
using namespace std;
const int Max=40000; //int 数组范围
int res[Max];
int main() {
int n;
clock_t start, finish; //主要保存起始时间和终止时间
double duration; //耗时
while(cin>>n && n>=0 && n<=10000){
start=clock();
memset(res,0,sizeof(res)); //初始化申请空间,并每位置0
res[0]=1; //0!=1
for(int i=1;i<=n;i++) //1~N
//carry为进位,初始进位为0,个位没有进位
for(int j=0,carry=0;j10;
res[j]=res[j]%10;
}
int i;
for( i=Max-1;i>=0;i--) if(res[i]) break;
//从后往前(高位到低位)求出不为0的一项,即结果的最高位
for(int j=i;j>=0;j--) //高位到低位输出
printf(j==0?"%d\n":"%d",res[j]);
finish=clock();
duration=(double)(finish-start)/CLOCKS_PER_SEC;//耗时
cout<"! 耗时"<"s"<return 0;
} 运行效果:
10000阶乘普通方法求解耗时:

500!:
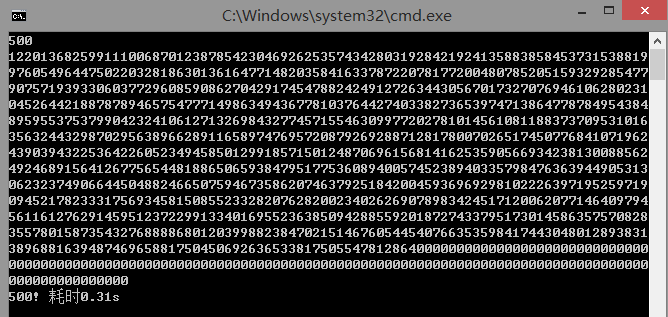
注意:
10000!的求解普通方法求解耗时是惊人的,要想AC过杭电acm1042题目必须优化,提高效率。一次优化:
for(int i=1;i<=n;i++) //1~N
//carry为进位,初始进位为0,个位没有进位
for(int j=0,carry=0;j*i+carry;
carry=res[j]/10;
res[j]=res[j]%10;
} 仔细观察可以发现,j的循环次数是可以减少的(j的次数是由i!的位数决定的,大家这里可以好好理解一下哈),因为这里每次j都要被执行Max次,然而我们发现N!的位数=[lg(1)+lg(2)+…..log(N)]+1([]表示向上取整),即每次j运行的次数只要满足N!的位数即可,这样可以提高效率,尤其是N很大的时候。所以用一个数组extra保存1~N的位数。废话不多说,直接上代码:
#include "! 耗时"<"s"<return 0;
} 运行效果:
10000阶乘优化后方法求解耗时,可以看出耗时减少一半:

500!:

二次优化:
for(int i=1;i<=n;i++)
//j<=(int)extra[i]+1;这句有效减少了次数
for(int j=0,carry=0;j<=(int)extra[i]+1;j++){
res[j]=res[j]*i+carry;
carry=res[j]/10;
res[j]=res[j]%10;
}继续看这段代码,这里是以10进位的,但是如果把它换成100、1000呢?
你就会发现,效率突然便高了,为什么呢?因为以前是以10进位,j会运行j<=(int)extra[i]+2次,如果以100或1000为基准呢,他会继续缩小原来的100或1000倍。这里测试取基准100000效果最佳,因为超过100000会出错。这样 次数 count=j<=(int)extra[i]+1/5;,为什么会是除以5呢,因为数组的一个元素可以保存5位,超过五位就进位。仔细想想,是不是还要取一次余是吧,因为要是除不尽5呢?其实这里已经包含了。废话不多说上代码:
#include double)(finish-start)/CLOCKS_PER_SEC;
cout<"s"<return 0;
} 运行效果:
是不是发现效率又高了很多???!!!!

500!:

杭电AC代码:
#include return 0;
} 另附杭电AC截图:
从上依此往下是第二次优化,网上其他博客代码运行,第一次优化。
这里是其中代码博客网址:
http://blog.csdn.net/lishuhuakai/article/details/8077688
这里就算是结束了,是不是觉得算法很有趣呢,我只是刚刚学了一点点,这里就班门弄斧了哈,如果有错误还请大家指出,第一次写算法博客,如果觉得对你有帮助的话还请评论下哈,谢谢。
