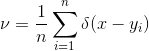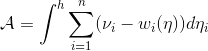本文授权转载自：老顾谈几何
作者：顾险峰
编辑：韩蕊
在过去的两三年中，对抗生成网络（Generative Adersarial Network GAN）获得了爆炸式的增长，其应用范围几乎涵盖了图像处理和机器视觉的绝大多数领域。其精妙独到的构思，令人拍案叫绝；其绚烂逼真的效果，令众生颠倒。一时间对抗生成网络引发了澎湃汹涌的技术风潮，纳什均衡的概念风靡了整个人工智能领域。
Goodfellow于2014年提出了GAN的概念，他的解释如下：GAN的核心思想是构造两个深度神经网络：判别器D和生成器G，用户为GAN提供一些真实货币作为训练样本，生成器G生成假币来欺骗判别器D，判别器D判断一张货币是否来自真实样本还是G生成的伪币；判别器和生成器交替训练，能力在博弈中同步提高，最后达到平衡点的时候判别器无法区分样本的真伪，生成器的伪造功能炉火纯青，生成的货币几可乱真。这种阴阳互补，相克相生的设计理念为GAN的学说增添了魅力。
GAN模型的优点来自于自主生成数据。机器学习的关键在于海量的数据样本，GAN自身可以生成不尽的样本，从而极大地减少了对于训练数据的需求，因此极其适合无监督学习；GAN的另外一个优点是对于所学习的概率分布要求非常宽泛，这一概率分布由训练数据的测度分布来表达，不需要有显式的数学表示。
GAN虽然在工程实践中取得巨大的成功，但是缺乏严格的理论基础。大量的几何假设，都是仰仗似是而非的观念；其运作的内在机理，也是依据肤浅唯像的经验解释。丘成桐先生率领团队在学习算法的基础理论方面进行着不懈的探索。我们用最优传输（Optimal mass Transportation）理论框架来阐释对抗生成模型，同时用凸几何（Convex Geometry）的基础理论来为最优传输理论建立几何图景。通过理论验证，我们发现关于对抗生成模型的一些基本观念有待商榷：理论上，Wasserstein GAN中生成器和识别器的竞争是没有必要的，生成器网络和识别器网络的交替训练是徒劳的，此消彼长的对抗是虚构的。最优的识别器训练出来之后，生成器可以由简单的数学公式所直接得到。详细的数学推导和实验结果可以在图7中找到。
下面，我们就这一观察展开详细论述。我们首先分析WGAN的理论框架；然后简介最优传输理论，解释生成器和判别器的主要任务；我们再介绍凸几何中的基本定理，解释凸几何和最优传输的内在联系，用计算几何的语言来解释最优传输框架下的基本概念；初步试验结果比较了WGAN和几何方法；最后我们进行一些扼要的讨论。
规模宏大的随机数生成器
大家对于随机数的生成原理耳熟能详，GAN本质上可以被视作是一个规模宏大的随机数生成器。我们考察最为简单的线性同余生成算法
这里
是比较大的整数，那么
构成了单位区间上的均匀分布（uniform distributed）伪随机数。我们再来生成单位圆盘上的高斯分布的随机采样点：首先生成
，然后定义映射
由此可见，我们可以通过一个变换将均匀分布变换成高斯分布。如果我们将概率分布看成是某种质量密度，映射会带来面积的变化，因此带来密度的变化，这样就从一种概率分布变换成另外一种概率分布。
图2. GAN本质上是将一种概率分布（高斯分布）变成另外一种概率分布（人脸图像）。
在图像生成应用中，GAN模型本质上就是将一种固定的概率分布，例如均匀分布或者高斯分布，变换成训练数据所蕴含的概率分布，例如人脸图像的分布。GAN的理想数学模型如下：我们将所有
图像构成一个空间，记为图像空间
，每一张图像看成是空间中的一个点，
。我们用
来表示图片
是否表达一张人脸的概率，那么
就是GAN要学习的目标概率测度。在工程实践中，我们只有一些人脸图像的样本
，这些样本构成了经验分布作为
的近似。经验分布的公式表达为：
绝大多数图片并不是人脸图像，因此
的支撑集合
是图像空间中的一个子流形，
的维数远远小于图像空间
的维数。支撑集流形的参数空间等价于特征空间，或者隐空间（latent space)
。编码映射（encoding map）就是将
映到特征空间，解码映射（decoding map）就是将特征空间映到支撑集流形。
图3. WGAN【3】的理论框架。
假设在隐空间有一个固定的概率分布
，例如高斯分布或者均匀分布。我们用一个深度神经网络
来逼近解码映射
，
将
映成了图像空间中的概率分布
我们称
为生成分布。判别器的核心任务是计算训练数据分布和生成分布
之间的距离；生成器的目的在于调节
使得生成分布
尽量接近数据分布。那么，如何计算分布间的距离呢？如何最优化映射呢？这需要用到最优传输理论。
最优传输理论梗概
给定带有概率测度的空间
和
，具有相同的总质量，
。一个映射
被称为是保持测度，如果对于一切可测集合
，我们都有
记为
。给定距离函数
，代表两点间的某种距离，传输映射的传输代价函数为：
蒙日问题 法国数学家蒙日于18世纪提出了最优传输映射问题：如何找到保测度的映射，使得传输代价最小，
这种映射被称为是最优传输映射（Optimal Mass Transportation Map）。最优传输映射对应的传输代价被称为是概率测度之间的Wasserstein距离：
Kantorovich 对偶问题 Kantorovich证明了蒙日问题解的存在性唯一性，并且发明了线性规划（Linear Programming），为此于1975年获得了诺贝尔经济奖。由线性规划的对偶性，Kantorovich给出了Wasserstein距离的对偶方法：
等价的，我们将
换成
的c-变换，
，那么Wasserstein距离为：
这里
被称为是Kantorovich势能
WGAN模型 在WGAN【3】中，判别器计算测度间的Wasserstein距离就是利用上式：这里距离函数为
，可以证明如果Kantorovich势能为1-Lipsitz，那么
。这里Kantorovich势能由一个深度神经网络
来计算，记为
。Wasserstein距离为
生成器极小化Wasserstein距离，
。所以整个WGAN进行极小-极大优化：
生成器极大化，判别器极小化，各自由一个深度网络交替完成。在优化过程中，解码映射
和Kantorovich势能函数
彼此独立。
Brenier方法 Brenier理论【4】表明，如果距离函数为 
，那么存在凸函数
，被称为是Brenier势能，最优传输映射由Brenier势能的梯度映射给出，
。由保测度条件
，Brenier势能函数满足所谓的蒙日-安培方程：
关键在于，Brenier势能和Kantorovich势能满足简单的关系：
。
判别器计算Kantorovich势能，生成器计算Brenier势能。在实际优化中，判别器优化后，生成器可以直接推导出来，不必再经过优化过程。
凸几何理论梗概
最优传输的Brenier理论和凸几何理论中的Alexandrov定理彼此等价，它们都由蒙日-安培方程来刻画。
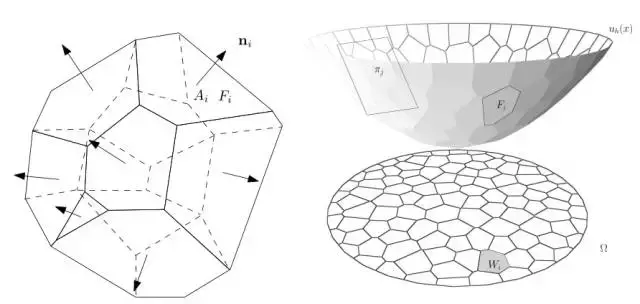
图4. Minkowski问题和Alexandrov问题
Minkowski 定理 如图4所示，左帧显示了经典的Minkowski定理：给定每个面的法向量和面积
，满足条件
，那么凸多面体
存在，并且彼此相差一个平移。这一定理在任意维欧氏空间都成立。
Alexandrov 定理 右帧显示了Alexandrov定理【2】：假设
是平面上的一个凸区域，
是开放凸多面体，每个面的法向量
给定，每个面在
上的投影面积
给定，满足
，那么凸多面体
存在，并且彼此相差一个垂直平移。这一定理在任意维欧氏空间都成立。Alexandrov于1950年代证明了这个定理，他的证明是基于代数拓扑的抽象存在性方法，无法转化成构造性算法。
变分原理 我们在【6】中给出了一个基于变分原理的构造性算法。假设第i个面的梯度
给定，高度
未知，这个面的方程为
。这些面的上包络（upper envelope）构成了Alexandrov凸多面体，也是凸分片线性函数
的图（graph），这里向量
代表所有支撑平面的高度。上包络
向平面投影，得到的一个胞腔分解，
胞腔
是第i个面在上的投影，其面积记为
。那么，我们定义Alexandrov势能为：
可以证明Alexandrov势能为凹函数，其极大值点给出的高度，就是Alexandrov定理中的解。
Alexandrov定理和最优传输
图5. Alexandrov定理和最优传输映射。
凸几何中的Alexandrov定理和最优传输理论中的Brenier定理本质是一致的，如图5所示，带测度的源区域为
，目标为带狄拉克测度的离散点集
,
我们构造一个Alexandrov凸多面体，每个面的投影面积满足 
，那么这个凸多面体对应的分片线性凸函数
就是Brenier势能函数，梯度映射
就是最优传输映射，Alexandrov势能函数就是传输代价，也等价于Wasserstein距离，即
。
计算几何的语言
图6. Power Diagram
Brenier定理和Alexandrov定理可以用计算几何中人所周知的Power Diagram语言来描述，这样有利于进一步理解和算法设计。如图6所示，我们为每个目标点
配上一个红色的小圆
，半径的平方被称为是power 权重。那么power距离定义为
由此，我们定义Power Diagram 
，这里
通过调节power 权重，我们可以使得每个胞腔的测度
等于
。综上所述，我们有如下最优传输的几何解释：
- 生成器：最优映射等价于Power胞腔分解，将每个胞腔
映到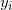
，请点击此处输入图片描述 - 判别器：Wasserstein距离中
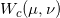中的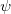
等于power 权重，请点击此处输入图片描述 - 判别器：Wasserstein距离Kantorovich势能
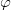等于power距离，
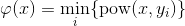请点击此处输入图片描述 - 生成器：Brenier势能等于Power Diagram的上包络。
初步实验设计和结果
WGAN的主要功能有两个：
1. 编码、解码实现从隐空间到图像空间的变换
2. 概率测度的变换
这两个任务都是高度非线性的，关于测度变换数学上已经建立了严格的基础理论，我们可以进行定量研究；关于从隐空间到图像空间的变换，目前的理论基础比较薄弱，我们只能进行定性比较。
为此，我们设计了两个尽可能简单的实验，来分别验证这两个功能：
测度变换实验 给定实验数据分布 
，我们的几何算法给出了精确解，我们试图用WGAN来解决同样的问题，进行详细比较。为了排除编码、解码映射的影响，我们设计隐空间和图像空间重合，因此WGAN只计算了测度变换。
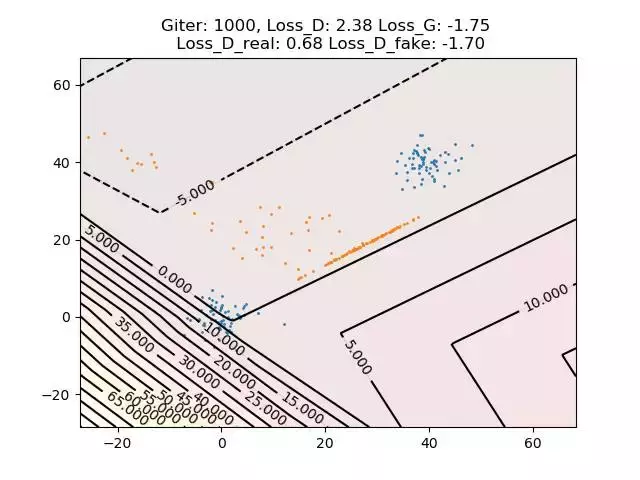
我们在这里，进行了两个实验，第一个实验的训练样本只有一个团簇，WGAN的生成分布和数据分布吻合得非常好。
图7. WGAN计算结果
为了可视化计算结果，我们在平面上设计了非常简单的实验，隐空间的概率分布为均匀分布。如图7所示，蓝色点代表数据样本，橙色点代表WGAN生成的样本。数据样本分成两个团簇，符合Gaussain Mixture的分布。我们看到WGAN最后的学习结果并不令人满意，橙色点的分布和蓝色点的分布相距甚远。
图8.几何方法计算结果
图8显示了几何方法生成的结果：每个胞腔映到一个具有同样颜色数据样本，上包络的面和它的投影胞腔具有同样的颜色。我们可以看到，首先最优传输映射将单位圆盘映射到所有的数据样本；其次，所有的power 胞腔都具有相同的面积，这意味着几何方法完美地生成了经验分布 
。我们注意到，Brenier势能函数（上包络）有一个尖脊，将梯度分成了两个团簇，因此能够处理多个团簇的分布逼近问题。
我们认为基本原因如下：WGAN用深度神经网络来构造测度变换映射，深度神经网络所能表达的函数为线性映射和ReLu的复合，因此必为连续映射。但是，由于数据样本构成为多个团簇，真正的最优传输映射必是非连续的映射，因此问题的解并不包含在深度神经网络构成的泛函空间中。
图9. 弥勒佛曲面
图10. 几何方法构造的编码映射：左侧是保角变换，右侧是保面积映射，两者之间相差一个最优传输映射。
解码映射 我们设计的第二个实验更为复杂。我们将三维欧氏空间
视为图像空间，弥勒佛曲面作为子流形，二维欧氏平面作为隐空间
。我们的目的是做一个生成器，生成在曲面上的均匀分布。这里，子流形的几何比较复杂，我们先用几何中的Ricci流【5】的方法计算编码映射，将曲面映入到特征空间上, 映射将曲面的面元映到隐平面上面, 诱导了平面上的测度由曲面的共形因子来描述，如图10左帧所示。然后，我们计算隐空间到自身的最优传输映射，将均匀分布映射到由曲面共形因子定义的概率测度（即曲面上的面元），这样就得到从曲面到隐平面的保面元映射，得到图10右帧所示。
图11. 共形映射诱导的曲面上非均匀分布。
图12. 最优传输映射诱导的曲面上均匀分布。
从图11我们看到，隐空间上的均匀分布被共形映射拉回到上，不再是均匀分布；图12显示，复合了最优传输映射之后，隐空间上的均匀分布被保面元映射拉回到上依然是均匀分布。由此，我们用几何方法构造了曲面上均匀分布的生成器。
但是，我们用同样的数据样本来训练WGAN模型，但是很难得到有意义的结果。如果读者有兴趣用其他深度学习模型进行研究探索，我们非常乐于分享这些数据，共同探讨提高。
讨论
在最优传输理论中，如果距离函数是
，这里
是严格凸的函数，那么判别器的Kantorovich势能函数蕴含着最优传输映射，因此判别器和生成器之间的竞争没有必要。生成模型的最终目的是生成的概率分布，对于同一个目标概率分布，有无穷多个传输映射都可以生成。我们可以选择计算最为简单的一个，即
距离所诱导的最优传输映射，因为这个映射具有鲜明的几何意义。
理论上，概率分布之间的变换可以在图像空间中完成，也可以在隐空间中完成。但是在实践中，隐空间的维数远低于图像空间，因此应该在隐空间中施行。因此，生成模型具有两个任务：一个是计算编码解码映射，另一个是概率分布变换。目前的模型，将这两个任务混同，因此难以分析。
- 我们的初步实验表明深度神经网络无法表达非连续映射，但是最优传输映射往往是有间断点的，因此目前的GAN模型需要进一步拓展。
- 对于降维的编解码映射，目前完备的基础理论尚未建立起来，很多方面比较含混原始，例如GAN的收敛性验证，收敛阶估计，误差分析和控制。
我们计划用更为精细的实验来详尽分析，更期待看到基础理论方面的长足发展。
小结
我们这里给出了最优传输映射观点下GAN模型的几何解释，指出了生成器和判别器之间的对抗竞争和交替训练可以被省略，而用显示的数学关系来取代。GAN模型主要任务分为编解码和概率测度变换，概率测度变换可以用透明的几何算法来解释并改进。初步试验结果显示了GAN模型构造的函数空间具有一定的局限性，无法表示经验数据的分布。
鸣谢
长期以来，丘成桐先生的团队坚持用几何的观点来阐述和改进深度学习模型。早在2017年2月初，笔者就撰文写了“看穿机器学习的黑箱”系列引起了很大的反响。许多学者和科研机构和团队成员联系，邀请我们前去给报告，我们将会在几个大会上详细解释我们的工作：全国计算机数学会议（10月20日，湘潭），2017中国计算机科学大会（10月26日，福州）第二届智能国际会议（10月27日，ICIS2017，上海）。我们和许多专家学者进行过讨论深入交流，特别是得到张首晟先生的鼓励，我们才总结成文，在此一并致以谢意！
最后，我们以张首晟先生的第一性原理来结束此文：“人类看到飞鸟遨游行空，便有了飞翔的梦想.但是早期的仿生却都失败了。理论物理指导我们理解了飞行的第一性原理，就是空气动力学，造出的飞机不像鸟却比鸟飞地更高更远。人工智能也是一样，人类的大脑给了我们智能的梦想，但不能简单地停留在神经元的仿生,而要理解智慧的第一性原理，才能有真正的大突破！”
References 1. Goodfellow, Ian J.; Pouget-Abadie, Jean; Mirza, Mehdi; Xu, Bing; Warde-Farley, David; Ozair, Sherjil; Courville, Aaron; Bengio, Yoshua (2014). "Generative Adversarial Networks". arXiv:1406.2661 2. A. D. Alexandrov. “Convex polyhedra” Translated from the 1950 Russian edition by N. S. Dairbekov, S. S. Kutateladze and A. B. Sossinsky. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2005.3. Martin Arjovsky, Soumith Chintala, and Léon Bottou. Wasserstein generative adversarial networks. In International Conference on Machine Learning, pages 214–223, 2017.4. Yann Brenier. Polar factorization and monotone rearrangement of vector-valued functions. Comm. Pure Appl. Math., 44(4):375–417, 1991.5. Xianfeng Gu, Feng Luo, Jian Sun, and Tianqi Wu. A discrete uniformization theorem for polyhedral surfaces. Journal of Differential Geometry (JDG), 2017.6. Xianfeng Gu, Feng Luo, Jian Sun, and Shing-Tung Yau. Variational principles for minkowski type problems, discrete optimal transport, and discrete monge-ampere equations. Asian Journal of Mathematics (AJM), 20(2):383 C 398, 2016.7. Na Lei,Kehua Su,Li Cui,Shing-Tung Yau,David Xianfeng Gu, A Geometric View of Optimal Transportation and Generative Model, arXiv:1710.05488.