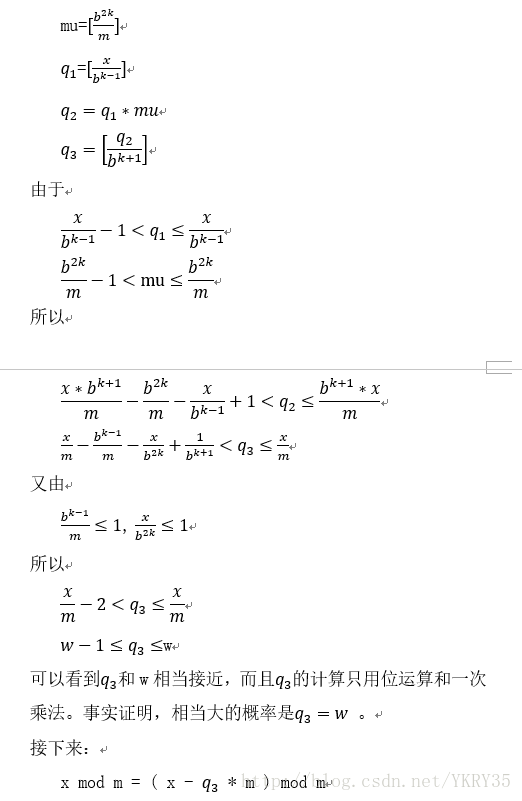大数取模运算Barrett reduction

Barrett reduction算法的证明和使用。

作者刚做完了课程设计作业，闲来无事写篇文章。

大数中的指数运算，需要对一个数进行取模，因为最大可能二进制下2048位的2048位次方，所以必须边做乘法边取模。

乘法使用快速幂，如果底数位数是x，指数位数是e，底数足够大的话，复杂度取决于模数，模数是m位的话，复杂度是O(m*m*e)。程序里，大数的存储是2的32次方进制的，这里的m*m要除以（32*32）。

取模运算，如果直接调用大数取模，因为除法是很慢的，所以效率很低。用Barrett reduction算法可以将除法转化为乘法和位运算，减法。

因为模数是任意的，所以不用蒙哥马利算法。

作业里只要求完成非负的大数运算，后面证明中默认大数都是非负的。

下面介绍Barrett reduction算法

求 x mod m

 m的位数是k

使用条件: x位数不大于2*k。对同一个数反复取模。

使用方法（这里是非负数）：

计算常量 mu=b^2k / m

取模时：

q1 = x / b^(k-1)

q2 = q1 * mu

q3 = q2 / b^(k+1)

r1 = x % b^(k+1)

r2 = (q3 * m) % b^(k+1)

r = r1 - r2

if ( r > m ) r -= m

return r

很多资料把mu=b^2k / m写成了mu=b^k / m，作者被坑了，很生气，决定放假写这么一个文章。另外，百度上基本看不到什么相关的证明。

证明：

 []表示取整，b是大数的进制

只需要一次除法预处理。

之后的除法和取模都是对进制b的若干次方进行的，所以位运算即可。

乘法时，因为最后结果是要取最后k+1位的，所以在乘的时候，可以直接把k+1位前面的丢弃，减少循环次数。作者是另外写了一个限制位数的乘法函数，效率提升了一些。

证明部分截图自word实验报告。