【R的机器学习】模型性能提升探索：R的其他神经网络包-neuralnet

上一节简单说明了神经网络，这里对R中进行神经网络算法的其他函数做下具体说明。

之前说到RSNNS包的神经网络，但是这个函数比较复杂，这里介绍下neuralnet包的神经网络。

这个包中的神经网络建模有个缺陷，只能对数值型的变量进行回归。也就是默认是无法进行分类变量的建模的，比如我们的iris数据集：

head(iris)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

最后一列：Species分成了三类，如果是一个，比如花期，然后这一列都是数值型变量，可以直接应用neuralnet，可是这里是因子型，需要手工进行转换成哑变量，或者简单理解，就是从分类数据新建几个列，按照T/F的形式进行结果储存。

这里需要用到一个哑变量转化的函数，这个函数在另一个神经网络包里（囧），首先载入两个包：

library(neuralnet)
library(nnet)

nnet里面的class.ind函数就是转化变量的工具，转化前：

head(iris_train$Species)
[1] versicolor setosa     setosa     versicolor setosa    
[6] virginica 
Levels: setosa versicolor virginica

转化后：

new<-class.ind(as.factor(iris_train$Species))
 head(new)
     setosa versicolor virginica
[1,]      0          1         0
[2,]      1          0         0
[3,]      1          0         0
[4,]      0          1         0
[5,]      1          0         0
[6,]      0          0         1

看到从一列变成了三列，而且只在列中是这一列的显示为1，其他都是0。这里就是一个典型的哑变量转换。

然后对这三个变量为结果建模：

iris_train1<-cbind(iris_train,new)
m_neuralnet<-neuralnet(setosa+versicolor+virginica~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,
                       data=iris_train1,hidden=1,
                       linear.output = FALSE,
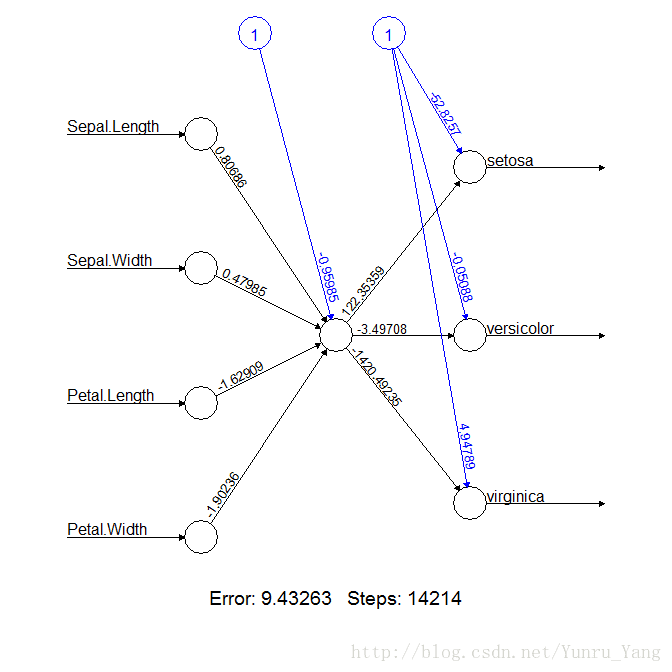
                       act.fct = "logistic")

其中的hidden就是层数，默认是1,看下图形：

plot(m_neuralnet)

这四个变量的权重也看到，并且看到误差平方和是9.4；

如果我们改变下层数，改成五层的话：

m_neuralnet<-neuralnet(setosa+versicolor+virginica~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,
                       data=iris_train1,hidden=5,
                       linear.output = FALSE,
                       act.fct = "logistic")
plot(m_neuralnet)

模型会变得非常复杂，而且误差平方和急剧减少。

其中的linear.output = FALSE 以及act.fct = "logistic" 都是默认选项，可以简单理解为让输出值为正；

既然我们这个五层的效果更好，我们就用这个看下准确率

m_neuralnet_result<-compute(m_neuralnet,iris_test[,1:4])
m_neuralnet_result$net.result

而出现了下面的情况：

head(m_neuralnet_result$net.result)
                                 [,1]          [,2]
27 1.00000000000000000000000000000000 0.05617862995
55 0.00000000000000000000003373619417 0.47955805769
71 0.00000000000000000000001592745084 0.48491407553
65 0.00000000000000000000062350814915 0.45879857510
87 0.00000000000000000000003974685356 0.47838856983
20 1.00000000000000000000000000000000 0.04237947425
                             [,3]
27 0.0000000000000000000000000000
55 0.0004919947855138113784398413
71 0.7496730095126287185536284596
65 0.0000000000000000009673689971
87 0.0000733587703406298521349380
20 0.0000000000000000000000000000

这个当然不是因子了，而且无法解释，其实是相当于我们把二分类进行logistic回归一样的感觉：logistic回归就是把原本的布尔值，改成了概率，那么原本为1的我们通过回归可以看到为1的概率。在这里，我们当然是取最大的那个概率作为我们的预测值；

m_neuralnet_result1<-max.col(m_neuralnet_result$net.result)

看到

 [1] 1 2 3 2 2 1 2 3 2 1 1 1 1 1 2 1 2 1 1 1 3 2 2 3 3 3 2 3
[29] 3 3 1 3 3 2 3 1 3 2 3 2 2 2 2 3 3

我们选取了最大的这一列，m_neuralnet_result1是列序号，我们需要还原为真实的变量名：

new_test<-class.ind(as.factor(iris_test$Species))
m_neuralnet_result2<-
  sapply(m_neuralnet_result1,function(x)colnames(new_test)[m_neuralnet_result1[x]])

这里用了一个sapply函数，也就是返回new_test的变量名；而new_test是什么呢？是用同样的方式针对iris_test的Species变量进行哑变量转换的数据。

看到

m_neuralnet_result2
 [1] "setosa"     "versicolor" "virginica"  "versicolor"
 [5] "versicolor" "setosa"     "versicolor" "virginica" 
 [9] "versicolor" "setosa"     "setosa"     "setosa"    
[13] "setosa"     "setosa"     "versicolor" "setosa"    
[17] "versicolor" "setosa"     "setosa"     "setosa"    
[21] "virginica"  "versicolor" "versicolor" "virginica" 
[25] "virginica"  "virginica"  "versicolor" "virginica" 
[29] "virginica"  "virginica"  "setosa"     "virginica" 
[33] "virginica"  "versicolor" "virginica"  "setosa"    
[37] "virginica"  "versicolor" "virginica"  "versicolor"
[41] "versicolor" "versicolor" "versicolor" "virginica" 
[45] "virginica" 

这个就是我们预测的变量结果啦。

下面还是老规矩，比较下预测值和实际值：

table(iris_test[,5],m_neuralnet_result2)

            m_neuralnet_result2
             setosa versicolor virginica
  setosa         13          0         0
  versicolor      0         16         1
  virginica       0          0        15

这里看到，准确率为97.8%，可以说是很高了；

然后看下Kappa值：

library(vcd)
Kappa(table(predict=m_neuralnet_result2,test=iris_test$Species))

value        ASE        z     Pr(>|z|)
Unweighted 0.9665179 0.03312992 29.17357 4.19822e-187
Weighted   0.9742416 0.02560386 38.05058  0.00000e+00

有96.7%的unweight值，迄今为止，应该是最高的了

最后说一句，理论上对于不同维度的数值需要进行标准化，但是本例中，由于四类数据差异不大，就省略了这个步骤，其实是不太严谨的。