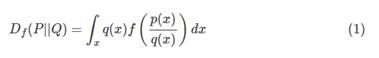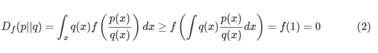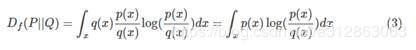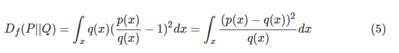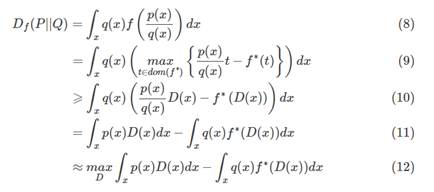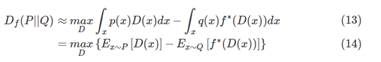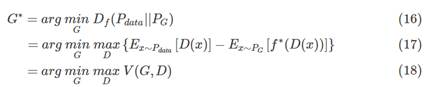【GANs学习笔记】（五）fGAN——深度理解GAN理论

完整笔记：http://www.gwylab.com/note-gans.html
——————————————————————-
本章借鉴内容：
https://alberthg.github.io/2018/05/13/wgan/

 

2. fGAN――深度理解GAN理论

    fGAN其实想要表达的就是一件事，不只是JS divergence，任何的divergence（统称为f-Divergence）都可以被放到GANs的架构中去。

我们先来看一下fGAN的证明（如果不感兴趣可以直接跳到△处）。

    设定P和Q是两个不同的分布， p(x)和 q(x)代表着分别从P和Q 采样出x的几率，则我们将f-Divergence 定义为：

上述公式衡量P和Q有多不一样，公式里边的函数f可以是很多不同的版本，只要 f满足以下条件：它是一个凸函数同时 f(1)=0 。

稍微分析一下这个公式：

?假设对于所有的 x来说，都有 p(x)=q(x)，则有(P,Q)=0，也就是意味着两个分布没有区别，和假设一样。

?同时 0 是能取到的最小值：

也就是说，只要两个分布稍有不同，就能通过 得到的正值反映出来。这个时候我们发现之前常用的 KL Divergence 其实就是 F Divergence 的一种。

    当你设置 f(x)=xlogx，即将 F Divergence 转换为了 KL Divergence 了。

当你设置 f(x)=−logx，即将 F Divergence 转换为了 Reverse KL Divergence。

当你设置 f(x)=，即将 F Divergence 转换为了 Chi Square。

 

    Fenchel 共轭(Fenchel Conjugate)

每一个凸函数f(x)都有对应的一个共轭函数取作(x)：

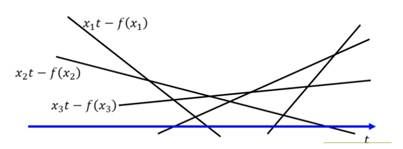
上述公式的意思就是给定 t 找出一个在 f(x)里边有定义的 x使得 xt−f(x) 最大，当然 t 可以无限取值，那么假定我们取值 t=t1和 t=t2则有：

对于所有可能的变量 t ，xt−f(x) 对应了无数条直线：

这个时候给定某个 t看看哪个 x可以取得最大值：

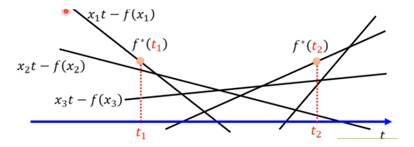
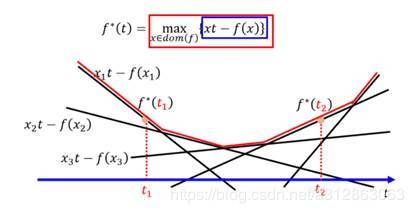
如上图，当 t=t1的时候，找到最大点 (t1)，当 t=t2的时候，找到最大点 (t2)，遍历所有的 t 即可得到红色的这条函数就是 (t)：

下面我们看一个具体一些的例子。

当 f(x)=x logx 时，我们可以将对应的(t)画出来：

这个图实际上是一个指数函数，当 f(x)=x logx 时，(t)=。

由于 ，假设让 g(x)=xt−x logx，那么现在的问题就变成了：给定一个 t时， 求 g(x)的最大值问题。对 g(x) 求导并让导数为 0：dg(x)/dx=t−logx−1=0，可解得x=。再带入回原公式可得：(t)=×t−×(t−1)=。

 

f-Divergence GAN

       那我们怎么用上边的数学知识和 GAN 联系在一起呢？ 我们首先要记得这条公式，关于 (t) 和 f(x)的转换关系式：

利用这个关系，我们能够将 F Divergence 的定义变形为一个类似于 GAN 的式子。

解释一下上式：

?第一行就是 F Divergence 的定义式；

?第三行将 t替换成 D(x) 并将 = 替换成 ⩾ 原因是：我们要求得的是给定 x找到一个 t使得式子最大，也就是说不管 D(x) 取什么值都一定小于或者等于第二行的式子；

?最后一步就是，我要找到一个 D 使得，式子最大，上界就是等于第二行的式子。

现在我们推导出关于 f Divergence 的变式：

       我们知道，GAN 的目的是训练生成器 G，使其产生的数据分布 与真实数据的分布 尽可能小。换言之，如果我们用 f-Divergence 来表达  与  的差异，则希望最小化。

       对于生成器来说，我们就是要找到一个 使得有：

       上述从数学推导上给出了 V(G,D) 的定义方式。但实际上要注意，此处的 V(G,D) 不一定就是原生GAN的形式。 f-Divergence GAN 是对 GAN 模型的统一，对任意满足条件的 f都可以构造一个对应的 GAN。

       综上便是fGAN的完整证明过程，原论文中还给出了各种不同的divergence function，想要使用不同的divergence距离直接选择其对应的函数即可：

△：如果上面的证明没有看懂完全没有关系，我们只需要记住，f-GAN告诉我们的就是一句话：不只是JS divergence，任何的divergence（统称为f-Divergence）都可以被放到GANs的架构中去。