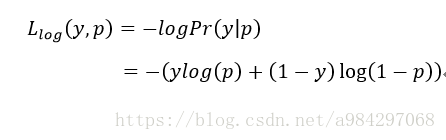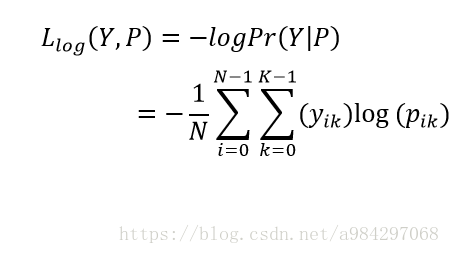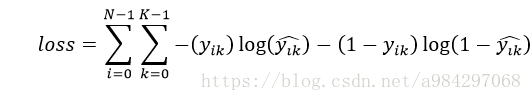深度学习(3)损失函数-交叉熵(CrossEntropy)
欢迎来到theFlyer的博客—希望你有不一样的感悟
前言：交叉熵损失函数。
1. 损失函数
机器学习算法都或多或少的依赖于对目标函数最大化或者最小化的过程，常常把最小化的函数称为损失函数，它主要用于衡量机器学习模型的预测能力。
损失函数可以看出模型的优劣，提供了优化的方向，但是没有任何一种损失函数适用于所有的模型。损失函数的选取依赖于参数的数量、异常值、机器学习算法、梯度下降的效率、导数求取的难易和预测的置信度等若干方面。
2. 交叉熵
对数损失Log Loss ，也被称为交叉熵损失Cross-entropy Loss，是定义在概率分布的基础上的。它通常用于多项式(multinomia)logistic regression 和神经网络，还有在期望极大化算法(expectation-maximization)的一些变体中。
对数损失用来度量分类器的预测输出的概率分布(predict_proba)和真实分布的差异，而不是去比较离散的类标签是否相同。
2.1任务为二分类时
在二分类的时候，真实标签集合为：Y∈{0,1}, 而分类器预测得到的概率分布：P = Pr(y=1)
那么，每一个样本的对数损失就是在给定真实样本标签的条件下，分类器的负对数似然函数，如下所示：
当某个样本的真实标签y=1时， Loss=−lop(p) L o s s = − l o p ( p ) ,分类器的预测概率p=Pr(y=1)的概率越小，则分类损失就越大；反之，分类器的预测概率p=Pr(y=1)的概率越大，则分类损失就越小。
对于真实标签y=0， Loss=−log(1−p) L o s s = − l o g ( 1 − p ) ,分类器的预测概率p=Pr(y=1)的概率越大，则损失越大。
例：预测为猫的p=Pr(y=1)概率是0.8，真实标签y=1；预测不是猫的1-p=Pr(y=0)概率是0.2，真实标签为0。
| * | 是猫 | 不是猫 |
|---|---|---|
| 标签 | 1 | 0 |
| 预测 | 0.8 | 0.2 |
此时损失为
2.2任务为多元分类时
在多元分类的时候，假定有k个类，则类标签集合就是labels=(1,2,3,…,k).如果第i个样本的类标签是k的话，就记为 yi,k=1 y i , k = 1 。采用one-hot记法。每个样本的真实标签就是一个one-hot向量，其中只有一个位置记为1。
例：设共有5类，label =3时，one-hot形式如下
| 标签 | one-hot |
|---|---|
| 3 | 00100 |
N个样本的真实类标签就是一个N行K列的矩阵：Y
| Y | class 0 | class1 | class1 |
|---|---|---|---|
| sample1 | 0 | 1 | 0 |
| sample2 | 1 | 0 | 0 |
| sample3 | 0 | 1 | 0 |
| sample4 | 0 | 0 | 1 |
| sample5 | 1 | 0 | 0 |
分类器对N个样本的每一个样本都会预测出它属于每个类的概率，这样的概率矩阵P就是N行K列的。
| P | class 0 | class1 | class1 |
|---|---|---|---|
| sample1 | 0.2 | 0.7 | 0.1 |
| sample2 | 0.5 | 0.2 | 0.3 |
| sample3 | 0.3 | 0.4 | 0.3 |
| sample4 | 0.2 | 0.3 | 0.5 |
| sample5 | 0.3 | 0.3 | 0.4 |
整个样本集合上分类器的对数损失就可以如下定义：
此时损失为
2.3任务为多标签分类时
多标签是在一种图片有多个类别时，比如一张图片同时有猫狗。
| * | 猫 | 狗 | 兔 |
|---|---|---|---|
| 标签 | 1 | 1 | 0 |
| 预测 | 0.8 | 0.7 | 0.1 |
与之前不一样的是，预测不再通过softmax计算，而是采用sigmoid把输出限制到(0,1)。正因此预测值得加和不再是1。这里交叉熵单独对每一个类别计算，每一个类别有两种可能的类别，即属于这个类的概率或不属于这个类的概率。
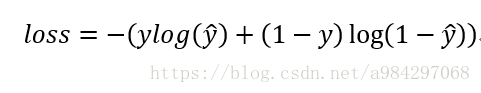
例：单张图片损失计算可以为
各类损失计算如下
对于整体损失可以用下式：
后记
人生如苦旅，我亦是行人。
个人公众号