深度学习－－手写数字识别＜二＞－－交叉熵损失函数(cross entropy cost function)

使用正确的代价函数避免学习减速

交叉熵损失函数(cross entropy cost function):

当激活函数采用sigmoid()函数，损失函数使用二次和成本函数时：

 C=12∥∥y−aL∥∥=12∑j(yj−aLj)2

其中：

 a=σ(z)

 z=∑jwjxj+b

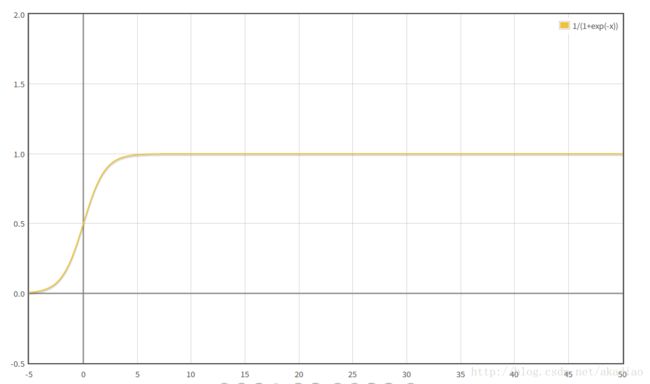
当输出值与目标值labels相差较大时，从sigmoid函数的图像上可以看出：

此时输出趋近于1且变化缓慢，即输出对weights和biases的偏导的值非常小，由weights和biases的更新公式可以看出：

 w′=w−η∂C∂w

 b′=b−η∂C∂b

此时weights和biases更新速度非常缓慢．

为解决神经网络学习慢的问题，引入交叉熵损失函数(cross entropy cost function)

 C=−1n∑x[ylna+(1−y)ln(1−a)))]

可以看出函数值大于等于0且当a=y时，cost=0;因此符合作为cost function的条件．
且可求得：

 ∂C∂wLjk=1n∑xaL−1k(aLj−yj)

 ∂C∂bLj=1n∑x(aLj−yj)

可以看出，此时学习的速度取决于：

 (aLj−yj)

因此，当偏差越大时学习较快，偏差小时学习较慢．

最大似然损失函数 log-likelyhood cost function：

softmax函数：

softmax是另为一种输出层方程：
神经元节点的带权输入Z为：

 ZLj=∑kwLjkaL−1k+bLj

softmax 输出为：

 aLj=ezLj∑kezLk

softmax输出值都是大于等于0，且总和等于1，故可看作是概率分布．

log-likelyhood cost function：

log-likelyhood cost function即最大似然损失函数．

 C=−lnaLy

可以看出当输出比较接近目标值时，概率a接近1，对数C接近0，反之概率较小时，对数C比较大．

分别对weights和biases求偏导：

 ∂C∂wLjk=aL−1k(aLj−yj)

 ∂C∂bLj=aLj−yj

可以看出此时学习速度同样取决与  (aLj−yj) ，因此不存在学习速度慢的问题．

code2:

#!/usr/bin/python
# coding:utf-8

import json
import random
import sys
import numpy as np

import cPickle
import gzip


def load_data():
    # 读取压缩文件,　返回一个描述符f
    f = gzip.open('../data/mnist.pkl.gz', 'rb')
    # 从文件中读取数据
    training_data, validation_data, test_data = cPickle.load(f)
    f.close()
    return (training_data, validation_data, test_data)


def load_data_wrapper():
    tr_d, va_d, te_d = load_data()
    # # 数据转换
    # tr_d是由50000个长度为784的numpy.ndarray组成的tuple
    # 转换后的training_inputs是由50000个长度为784的numpy.ndarray组成的list
    training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
    training_results = [vectorized_result(y) for y in tr_d[1]]
    # 训练集　training_data
    # zip()返回一个列表的元组，其中每个元组包含从每个参数序列的第i个元素。
    training_data = zip(training_inputs, training_results)
    validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
    # 验证集　validation_data
    validation_data = zip(validation_inputs, va_d[1])
    test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
    # 测试集　test_data
    test_data = zip(test_inputs, te_d[1])
    return (training_data, validation_data, test_data)



# 当预测值与目的值偏差较大时，会导致学习速度降低，故引入Cross　Entropy　Cost＝-[sum(y*loga + (1-y)log(1-a))]/n
# 交叉熵成本函数
class CrossEntropyCost(object):
    @staticmethod
    def fn(a, y):
        # 使用0代替数组x中的nan元素，使用有限的数字代替inf元素
        # sum(-ylog(a)-(1-y)log(1-a))
        return np.sum(np.nan_to_num(-y*np.log(a)-(1 - y)*np.log(1 - a)))
    # 返回从输出层的误差Δ,注意参数Z不使用的方法
    @staticmethod
    def delta(z, a, y):
        return (a-y)


# 定义二次和成本函数
class QuadraticCost(object):
    # 返回与输出相关联的成本
    @staticmethod
    def fn(a, y):
        return 0.5*np.linalg.norm(a-y)**2
    # 返回从输出层的误差Δ
    @staticmethod
    def delta(z, a, y):
        return (a-y) * sigmoid_prime(z)


class Network(object):
    def __init__(self, sizes, cost=CrossEntropyCost):
        # 获取神经网络的层数
        self.num_layers = len(sizes)
        # sizes即每层神经元的个数
        self.sizes = sizes
        # 赋随机值（服从高斯分布）,对权重和偏向进行初始化
        # 　bais从第2行开始
        self.default_weight_initializer()
        # 　zip从传入的可循环的两组量中取出对应数据组成一个tuple
        self.cost = cost
    # 计算对应的偏导数  x-784维　y-10维
    def backprop(self, x, y):
        # 返回一个元组（nabla_b，nabla_w）代表成本函数C_x的渐变。
        # nabla_b和nabla_w是numpy数组np.array的逐层列表,类似于self.biases和self.weights.
        # 分别生成与biases　weights等大小的0矩阵
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # 激活项 直接传入训练实例x的值
        activation = x
        # 逐层存储所有的激活(不止输入层),作为一个列表
        activations = [x]
        # 逐层存储所有中间向量z，,作为一个列表
        zs = []
        for b, w in zip(self.biases, self.weights):
            # 计算中间变量  Z=W*X+b
            z = np.dot(w, activation)+b
            # 列表存储所有中间向量z
            zs.append(z)
            # 激活activation=sigmoid(W*X+b)
            activation = sigmoid(z)
            # 列表存储所有的激活
            activations.append(activation)
        # 反向更新

        #     # 输出层
        # 计算输出层error=Oj(1-Oj)(Tj-Oj);
        # cost_derivative(activations[-1], y)即C对a的梯度:(Tj-Oj)即(activations[-1]-y)
        # sigmoid_prime(zs[-1])即:Oj(1-Oj)
        delta = (self.cost).delta(zs[-1], activations[-1], y)
        # 更新输出层的nabla_b,nabla_w
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())

        #     # 隐藏层
        # l = 1表示神经元的最后一层,l = 2是第二层,依此类推.反向更新直到初始层
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            # weights[-l + 1]即下一层的权重
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            # 输出C对w,b的偏导
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

    # epochs训练多少轮, mini_batch_size抽取多少实例,eta学习率
    def SGD(self, training_data, epochs, mini_batch_size, eta,
            # lmbda-正则化参数
            lmbda = 0.0,
            evaluation_data=None,
            monitor_evaluation_cost=False,
            monitor_evaluation_accuracy=False,
            monitor_training_cost=False,
            monitor_training_accuracy=False):
        # 验证集实例数量
        if evaluation_data:
            n_data = len(evaluation_data)
        n = len(training_data)
        evaluation_cost, evaluation_accuracy = [], []
        training_cost, training_accuracy = [], []
        # j代表第几轮,共epochs轮
        for j in xrange(epochs):
            # 将training_data中的数据随机打乱
            random.shuffle(training_data)
            # mini_batchs每次抽取mini_batch_size大小的数据作为一小块,从0到n每次间隔mini_batch_size张图片
            mini_batches = [training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)]

            # 对取出来的mini_batchs逐个进行更新
            for mini_batch in mini_batches:
                # 更新weights和biases
                self.update_mini_batch(mini_batch, eta, lmbda, len(training_data))
            print "Epoch %s training complete" % j

            if monitor_training_cost:
                cost = self.total_cost(training_data, lmbda)
                training_cost.append(cost)
                print "Cost on training data: {}".format(cost)
            if monitor_training_accuracy:
                accuracy = self.accuracy(training_data, convert=True)
                training_accuracy.append(accuracy)
                print "Accuracy on training data: {} / {}".format(accuracy, n)

            if monitor_evaluation_cost:
                # 验证集损失
                cost = self.total_cost(evaluation_data, lmbda, convert=True)
                evaluation_cost.append(cost)
                print "Cost on evaluation data: {}".format(cost)
            if monitor_evaluation_accuracy:
                # 验证集准确率
                accuracy = self.accuracy(evaluation_data)
                evaluation_accuracy.append(accuracy)
                print "Accuracy on evaluation data: {} / {}".format(accuracy, n_data)
        return evaluation_cost, evaluation_accuracy, training_cost, training_accuracy


    # eta:学习率  n:训练集实例数量
    # 传入单个的mini_batch,根据其x.y值，对整个神经网络的wights和biases进行更新
    def update_mini_batch(self, mini_batch, eta, lmbda, n):
        # 初始化
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            # 计算对应的偏导数
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        # 权重weights更新　W'k=(1-(eta*lmbda/n))W-(eta/n)&C/&Wk
        self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)]
        # 偏向biases更新  b'k=bk-(ets/n)&C/&bk
        self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)]

    # 赋随机值（服从标准正太分布）,对权重和偏向进行初始化
    def default_weight_initializer(self):
        # 第一层为输入层不设置偏差，从第二行开始
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        # 在同一个神经元的权值的平方根的平方根上用高斯分布平均0和标准偏差1初始化每个权值
        self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]

    # 使用平均0和标准差1的高斯分布初始化权重
    def large_weight_initializer(self):
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]

    # 准确率
    def accuracy(self, data, convert=False):
        if convert:
            # argmax()返回沿轴最大值的索引
            results = [(np.argmax(self.feedforward(x)), np.argmax(y)) for (x, y) in data]
        else:
            results = [(np.argmax(self.feedforward(x)), y) for (x, y) in data]
        return sum(int(x == y) for (x, y) in results)


    # 如果数据集是训练集(通常情况)设置为false,验证集或测试集,则为true
    def total_cost(self, data, lmbda, convert=False):
        cost = 0.0
        for x, y in data:
            a = self.feedforward(x)
            if convert:
                y = vectorized_result(y)
            # fn(a, y)=sum(-ylog(a)-(1-y)log(1-a)) 则cost=fn(a, y)/n
            cost += self.cost.fn(a, y)/len(data)
        # 加上正则化项　L2-regularization　训练集包含实例个数：len(data)  正则化项 (lmbda/2n)*sum(w**2)
        cost += 0.5*(lmbda/len(data))*sum(np.linalg.norm(w)**2 for w in self.weights)
        return cost


    # 根据当前输入利用sigmoid函数来计算输出
    def feedforward(self, a):
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a


    # 保存神经网络文件filename
    def save(self, filename):
        data = {"sizes": self.sizes,
                "weights": [w.tolist() for w in self.weights],
                "biases": [b.tolist() for b in self.biases],
                "cost": str(self.cost.__name__)}
        f = open(filename, "w")
        json.dump(data, f)
        f.close()

# sigmoid函数
def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

# sigmoid函数的导数
def sigmoid_prime(z):
    return sigmoid(z) * (1 - sigmoid(z))


#　向量化
def vectorized_result(j):
    e = np.zeros((10, 1))
    e[j] = 1.0
    return e



# 从filename加载神经网络，返回一个神经网络实例
def load(filename):
    f = open(filename, "r")
    data = json.load(f)
    f.close()
    cost = getattr(sys.modules[__name__], data["cost"])
    net = Network(data["sizes"], cost=cost)
    net.weights = [np.array(w) for w in data["weights"]]
    net.biases = [np.array(b) for b in data["biases"]]
    return net



if __name__ == '__main__':
    training_data, valivation_data, test_data =load_data_wrapper()

    # # 显示图像
    # ShowImage()static_foo


    net = Network([784, 30, 10])
    # 训练集training_data,训练10轮,每次取样10个作为mini_batch,学习率为3
    net.large_weight_initializer()
    # 用cross-entropy来识别MNIST数字

    times =400
    evaluation_cost, evaluation_accuracy, training_cost, training_accuracy = \
    net.SGD(training_data[:1000], times, 10, 0.5, evaluation_data=test_data,
            monitor_evaluation_accuracy=True, monitor_training_cost=True)


    import matplotlib.pyplot as plt
    temp = np.tile(100.0,times)
    evaluation_accuracy = evaluation_accuracy / temp
    x = np.arange(1, times+1, 1)
    fig = plt.figure()
    ax1 = fig.add_subplot(2,1,1)
    ax1 = plt.plot(x, evaluation_accuracy, 'g-', linewidth=2)
    plt.ylabel('evaluation_accuracy: %')
    plt.xlabel('Epoch')
    plt.grid()

    ax2 = fig.add_subplot(2,1,2)
    ax2 = plt.plot(x, training_cost, 'r-', linewidth=2)
    plt.ylabel('training_cost')
    plt.xlabel('Epoch')
    plt.grid()
    plt.show()

输出：

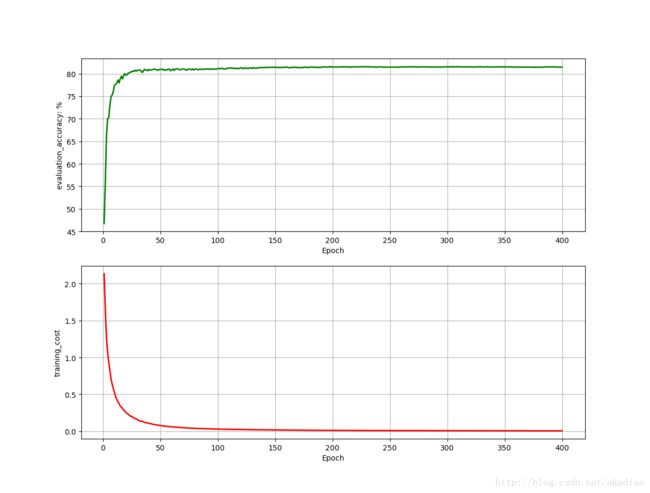
使用训练集中的前1000张图像training_data[:1000]进行训练，从图像中可以看到当训练100轮左右时，神经网络在测试集上的准确率已经达到100％，即已经发生了overfitting.即神经网络在训练集表现很好，但不能泛化到测试集上．
此时增大训练集可以帮助减少overfitting．

使用验证集防止overfitting

一般情况下，最好的降低过拟合的方法之一就是增加训练样本的量．但实际中增加训练样本的成本一般较高，因此可以采取其他方法来防止过拟合的发生，如使用验证集．
使用验证集，即在原训练集数据中预留出一部分数据作为内部的验证和评价．在每个迭代期的最后都计算在验证集上的分类准确率，一旦分类准确率已经饱和就停止训练．