Stata: 拉索回归和岭回归 (Ridge, Lasso) 简介
作者:王翰洋 (北京大学)
Stata 连享会: 知乎 | 简书 | 码云 | CSDN
连享会现场班精品课程……
文章目录
- 连享会现场班精品课程……
- 1. Ridge回归
- 2. Lasso 回归
- 3. 演示数据集
- Stata 相关命令
- 相关链接
- 关于我们
- 联系我们
- 往期精彩推文
「不显著」是很多跑回归的人的痛处,但有时不显著并非是故事本身的原因,而是多重共线性导致的。多元分析中,当两个或更多的变量出现相关的时候,就有可能出现多重共线性问题。一般的多重共线性并不影响估计,但高度的共线性会使估计的方差膨胀,t 值缩水,导致统计推断失效。
本文介绍了两种经典的筛选变量、应对多重共线性的参数方法,「Ridge 回归」和「Lasso 回归」。
1. Ridge回归
Ridge 回归 (Hoerl and Kennard, 1970) 的原理和 OLS 估计类似,但是对系数的大小设置了惩罚项。具体来说,
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \min_{\beta} (…
其中,t 代表惩罚的力度,t 越大,对系数的大小惩罚越重,约束越紧。取系数的平方和形式可以避免正负系数相抵消的情况。在矩阵形式中,Z 按照传统是标准化之后的(均值为 0,方差为 1),y 也需要中心化。不难证明,这个优化问题的解是:
β r i d g e = ( z T z + λ I p ) − 1 z T y {\beta}^{ridge}=(z^{T}z+\lambda I_{p})^{-1}z^{T}y βridge=(zTz+λIp)−1zTy
显然,λ 是这个问题的调整参数,当 λ 趋于 0 的时候,就退化为一般的 OLS 估计。当 λ 趋于正无穷的时候, 则是纯截距回归。实践中,可以通过交叉验证(cross validation)的方法来选择调整参数 λ 。在 Stata 命令中,可以通过命令 rxridge 来实现 Ridge 回归。命令基本格式是:
rxridge y X_1 X_2 X_3 [if exp] [in range] ///
[, msteps(#) qshape(#) rescale(#) tol(#) ]
具体说明如下:
msteps代表共线性容忍参数每增加一单位所带来的步数变化qshape控制了沿似似然空间收缩的形状rescale是调整方差的参数,比如 rescale(1) 就是让所有中心化变量方差都为 1 ,rescale(0) 就是让所有变量都保持原来的方差tol(#)用于设定收敛判据
2. Lasso 回归
Lasso 也是对系数的大小设置了惩罚项,但惩罚项引入的方式略不同,具体来说,
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \min_{\beta} (…
等价地,我们可以用以下损失函数来表示:
P R S S ( β ) = ( y − z β ) T ( y − z β ) + λ ∥ β ∥ 1 PRSS(\beta)=(y-z\beta)^{T}(y-z\beta)+{\lambda} \| {\beta} \|_{1} PRSS(β)=(y−zβ)T(y−zβ)+λ∥β∥1
仍然,λ 是这个问题的调整参数,不过一般情况下我们无法得到 β 的显示解。但是,当数据矩阵中各变量都相互正交且模为 1 时,我们可以得到 Lasso 的显示解。在 Lasso 中,可以看到,惩罚项由平方换成了绝对值。虽然绝对值是凸函数,函数在 0 点有唯一的最小值,但其在此点不可导。当某项的惩罚系数足够大时,那么它将无法进入模型(变量选择),只有那些回归系数非0的变量才会被选入模型。
在 Stata 中,我们可以安装 lassopack 命令来实现 Lasso 回归,Lassopack 包含三个与 Lasso 相关的子命令(输入 help lassopack 可以查看详情):
- 子命令
lasso2可进行Lasso估计; - 子命令
cvlasso可进行 K 折交叉验证(k-fold cross validation); - 子命令
rlasso可以估计惩罚项由数据决定或者高维情形(变量维度超过样本数)。
3. 演示数据集
下面我们用一个糖尿病数据集(Efron et al., 2004)来演示 Ridge 回归和 Lasso 回归,
这个数据集包括血液化验等指标(Source:http://CRAN.R-project.org/package=lars)。除了被解释变量 y 之外,还有 X 和 X2 两组变量,前者是标准化后的,为 442x10 维矩阵,后者包括前者及一些交互作用,为 442x64 维矩阵,我们考虑 y 和 X2 。在导入数据后,我们先进行 Ridge 回归。输入命令
rxridge y x2*, q(-1)
就可以得到 Ridge 回归的结果,估计的 sigma 为 0.690,最后迭代出的 MCAL 为 63,Summed SMSE 为 104.37。
然后我们考虑 Lasso 回归。输入如下命令可以进行 Lasso 估计,最后一个选项代表显示整个解的路径:
lasso2 y x2* , plotpath(lambda)
下表显示随着调整参数λ由大变小,越来越多的变量进入模型,比如 λ=3.992e+04 时,常数项首先进入模型。

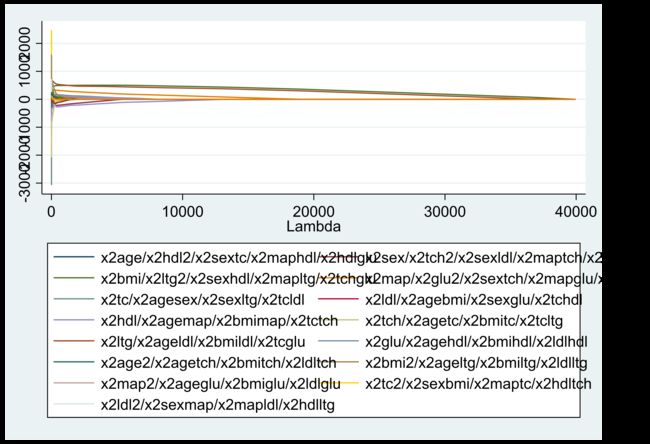
下图为整个解的路径(作为 λ 的函数),画出了不同变量回归系数的变化过程。其中,当 λ=0 时(下图最左边),不存在惩罚项,故此时 Lasso 等价于OLS。而当 λ 很大时(下图最右边),由于惩罚力度过大,所有变量系数均归于 0 。这里,由于变量非常多,整个图颇有野兽派风格:
紧接着,我们使用 K 折交叉验证的方法来选择最佳的调整参数。所谓的 K 折交叉验证,是说将样本数据随机分为 K 个等分。将第 1 个子样本作为 “验证集”(validation set)而保留不用,而使用其余 K-1 个子样本作为 “训练集”(training set)来估计此模型,再以此预测第 1 个子样本,并计算第1个子样本的 “均方预测误差”(Mean Squared Prediction Error)。其次,将第 2 个子样本作为验证集,而使用其余 K-1 个子样本作为训练集来预测第2个子样本,并计算第 2 个子样本的 MSPE。以此类推,将所有子样本的 MSPE 加总,即可得整个样本的 MSPE。最后,选择调整参数 ,使得整个样本的 MSPE 最小,故具有最佳的预测能力。我们输入命令
cvlasso y x2*, lopt seed(123)
其中,选择项 “lopt” 表示选择使 MSPE 最小的 λ,选择项 “seed(123)” 表示将随机数种子设为 123(可自行设定),以便结果具有可重复性;默认 K=10(即 10 折交叉验证)。
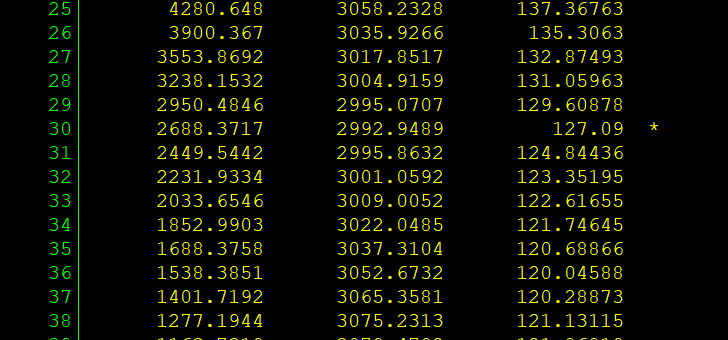
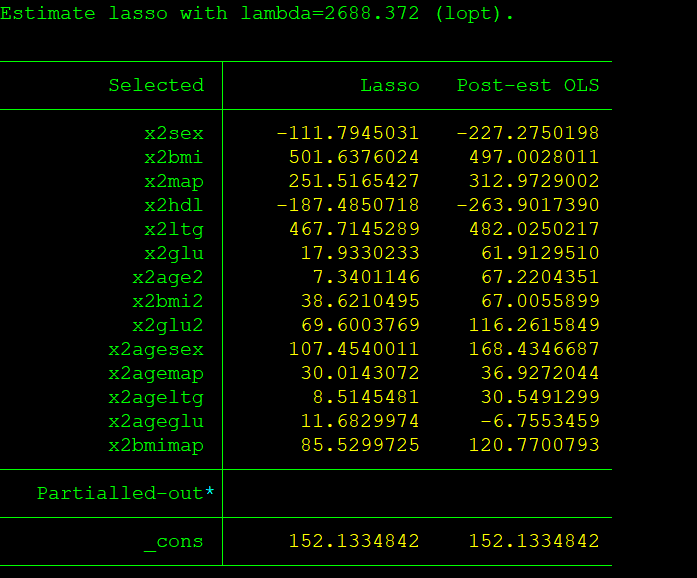
打星号处的 λ=2688.3717,这是使 MSPE 最小的调整参数,与此对应的估计结果如下图所示:
上表右边第 1 列即为 Lasso 所估计的变量系数。其中,除常数项外,只有 14 个变量的系数为非零,而其余变量(未出现在表中)的系数则为 0。考虑到作为收缩估计量的 Lasso 存在偏差(bias),上表右边第 2 列汇报了 “Post Lasso” 估计量的结果,即仅使用 Lasso 进行变量筛选,然后扔掉 Lasso 的回归系数,再对筛选出来的变量进行 OLS 回归。
通过以上的介绍,我们已经掌握了如何使用 Stata 进行 Ridge 回归和 Lasso 回归,这是经典的解决高度共线性、筛选变量的方法。但是,近年来非常火热的机器学习方法,在解决高度共线性、筛选变量方面,有更好的表现,期待看到更多的关于机器学习方法的 Stata 命令。
Stata 相关命令
这些都是外部命令,可以使用 findit cmdname 搜索后下载,亦可直接使用 ssc install cmdname, replace 直接下载,详情参见 「Stata: 外部命令的搜索、安装与使用」。
help ridgereg// module to compute Ridge Regression Modelshelp elasticregress//perform elastic net regression, lasso regression, ridge regression, 作者自己的评价help ridge2sls// Two-Stage Least Squares (2SLS) Ridge & Weighted Regressionhelp lassopack//module for lasso, square-root lasso, elastic net, ridge, adaptive lasso estimation and cross-validation- lassopack 项目主页 - The Stata Lasso Page
- 作者 PPT
相关链接
- Wieringen, 2018, PDF book Lecture notes on ridge regression
- Stanfor PPT - Regularization: Ridge Regression and the LASSO - Stanford Statistics
- 脊回归(Ridge Regression)
- lixintong1992-Ridge Regression || 从收缩的角度解释的很好
- 岭回归(ridge regression) || 非矩阵方式表述,更容易理解
- scikit-learn v0.20.2 - Ridge Regression
- Ridge回归、Lasso回归、坐标下降法、最小角回归
- 一文读懂正则化与LASSO回归,Ridge回归
- 七种常见的回归分析
- Colin Cameron, 2017, PPT, Machine Learning for Microeconometrics || 介绍了 cross-validation, lasso, regression trees and random forests 等方法
- Ridge Regression,这个页面提供了参考文献
关于我们
- 【Stata 连享会(公众号:StataChina)】由中山大学连玉君老师团队创办,旨在定期与大家分享 Stata 应用的各种经验和技巧。
- 公众号推文同步发布于 CSDN-Stata连享会 、简书-Stata连享会 和 知乎-连玉君Stata专栏。可以在上述网站中搜索关键词
Stata或Stata连享会后关注我们。 - 点击推文底部【阅读原文】可以查看推文中的链接并下载相关资料。
- Stata连享会 精彩推文1 || 精彩推文2
联系我们
- 欢迎赐稿: 欢迎将您的文章或笔记投稿至
Stata连享会(公众号: StataChina),我们会保留您的署名;录用稿件达五篇以上,即可免费获得 Stata 现场培训 (初级或高级选其一) 资格。 - 意见和资料: 欢迎您的宝贵意见,您也可以来信索取推文中提及的程序和数据。
- 招募英才: 欢迎加入我们的团队,一起学习 Stata。合作编辑或撰写稿件五篇以上,即可免费获得 Stata 现场培训 (初级或高级选其一) 资格。
- 联系邮件: [email protected]
往期精彩推文