神经网络模型的各种优化算法
1.批量梯度下降算法(Batch Gradient Descent)
思想:基于整个训练集的损失迭代更新梯度。
优点:
1. 由于梯度更新考虑的是全局的损失,所以不会陷入局部最优;
缺点:
1. 由于计算的是整个训练集的损失,所以每次迭代的计算量较大,占用内存大;
公式理解:
更新参数向使得损失减小的方向变化。
2.随机梯度下降算法
思想:基于随机选取的一个样本迭代更新梯度。
优点:
- 由于计算的是单个训练样本的损失,所以计算量较小;
缺点:
- 由于考虑的仅是单个样本的梯度,所以容易陷入局部最优;
- 由于引入了噪声,所以具有正则化的效果;
- 对于参数较为敏感,所以参数初始化很重要;
- 当样本集较大时,训练时间长;
- 选择合适的学习率比较困难;
公式理解:
更新参数向使得损失减小的方向变化。
3.mini批量梯度下降算法(Mini Batch Gradient Descent)
思想:中和以上两种算法,基于指定的batch size个样本迭代更新梯度。
优点:
1. 对于很大的数据集,能够以较快的速度收敛,提升训练速度;
缺点:(以上两个算法也具有这些缺点)
1. 当梯度有误差时,需要逐渐减小学习率,否则无法收敛;
2.梯度的更新方向完全依赖于当前batch个样本的梯度,所以梯度更新方向不稳定;
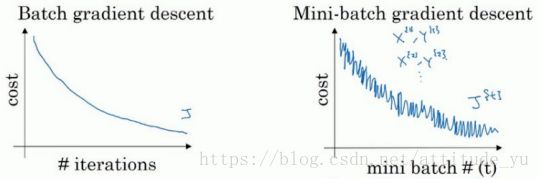
如图所示,批量梯度下降相较于mini批量梯度下降损失曲线更光滑,即振荡幅度小。
公式理解:
更新参数向使得损失减小的方向变化。
4.动量梯度下降
思想:基于之前梯度的方向和当前batch的梯度方向迭代更新梯度。
优点:
- 梯度更新初期,前后的梯度方向一致,加速梯度更新力度,即加速收敛;
- 当当前batch的梯度方向发生改变时,能够在一定程度上抑制震荡,从而加速收敛;
- 当当前batch的梯度很小时,由于考虑了之前的梯度,所以会增大更新幅度,从而有助于跳出局部最优。
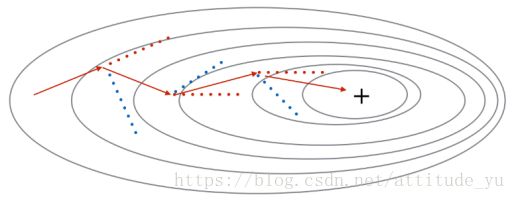
如图所示,动量梯度下降算法很好的抑制了梯度的振荡,从而加速收敛。
公式理解:
基于动量修正当前的梯度方向,更新参数向使得损失减小的方向变化。
5.Nesterov Accelerated Gradient
思想:首先利用之前梯度更新方向获得未来的更新参数,然后继续更新此未来参数,获得其梯度,最终联合计算之前梯度和未来参数的梯度为当前batch的梯度更新方向。
优点:
1. 基于动量梯度方向进行预测更新当前梯度方向,避免了当前梯度过快的前进;
如图所示,以上两种方法对于当前batch的梯度更新方向所考虑的梯度方向不同。
公式理解:
基于动量和未来梯度方向修正当前的梯度方向,更新参数向使得损失减小的方向变化。
6.AdaGrad
思想:累计计算每次迭代每个参数梯度的平方和,用基础学习率除以此累计值得开方,从而实现学习率的动态更新,所以其不仅考虑了梯度随时间(迭代次数)的变化,还考虑了参数状态的变化(当前梯度与之前梯度的变化差异)。
优点:
- 训练前期,累计值较小,梯度更新幅度大;
- 训练后期,累计值增大,梯度更新幅度小,实现了对学习率更新幅度的约束;
- 适合处理稀疏梯度(当神经元进入relu激活函数的负饱和区,其就不会进行梯度更新,即稀疏梯度);
缺点:
- 训练后期,累计值非常大,导致学习率会非常小,从而使得模型基本不会进行梯度更新;
- 仍然需自定义全局学习率;
由公式可知,当前batch的梯度更新大小与一次梯度成正比,与二次梯度的累加和成反比,即基于二次逼近公式更新梯度。AdaGrad是利用之前的一次梯度去估计二次梯度。
公式理解:
更新参数向使得损失减小的方向变化,基于时间和参数状态动态更新参数变化的步长。
7.RMSprop
思想:对AdaGrad中对之前梯度的权重是相同的改进,引入指数加权平均,即给予更接近当前梯度的梯度更大的权重。
公式理解:
更新参数向使得损失减小的方向变化,基于远近时间和远近参数状态动态更新参数变化的步长。
8.Adam(adaptive momentum estimation)
思想:结合了RMSprom和动量算法,利用梯度的一阶矩估计和二阶矩估计调整每个参数的学习率,其在经过偏置校正后,使得每一次迭代学习率都有个确定范围(进行了动态约束),使得参数较为平稳。
优点:
- 结合了AdaGrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点;
- 高效计算;所需内存小;
- 为不同的参数计算不同的自适应学习率;
- 适用于大数据集和高维度空间;
公式理解:
更新参数向使得损失减小的方向变化,基于远近时间和远近参数状态动态更新参数变化的步长。
9.Adamx
思想:对Adam的改进,将每一次迭代学习率确定范围的上限简单化。
10.总结
- 对于稀疏数据,尽量使用学习率可自适应的优化方法,采用默认值;
- 学习率自适应的优化方法更适合于快速收敛,模型较复杂的网络;
11.python 伪代码
import numpy as np
def SGD(learning_rate, dx , x):
x = x - learning_rate*dx
return x
def momentum_GD(learning_rate, dx, x, alpha,momentum):
momentum = alpha*momentum - learning_rate*dx
x = x - momentum
return x,momentum
def Nesterov_momentum_GD(learning_rate, dx, x, alpha,momentum):
x_ahead = x + alpha*momentum
momentum = alpha*momentum - learning_rate*dx_ahead
x = x - momentum
return x,momentum
def AdaGrad(Dx, learning_rate, dx, x):
Dx = Dx + (dx)**2
x = x - learning_rate*(dx/(np.sqrt(Dx)+0.0001))
return x,Dx
def RMSprop(Dx, learning_rate, dx, x, belta):
Dx = belta*Dx + (1-belta)*(dx)**2
x = x - learning_rate*(dx/(np.sqrt(Dx)+0.0001))
return x,Dx
def Adam(mt,vt,learning_rate, dx, x, belta1, belta2, t):
mt = belta1*mt + (1-belta1)*dx
vt = belta2*vt + (1-belta2)*(dx)**2
mt_ = mt/(1-belta1**t)
vt_ = vt/(1-belta2**t)
x = x - learning_rate*mt_/(np.sqrt(vt_)+0.0001)
return x,mt,vt参考资料:
1. 神经网络优化算法综述
https://blog.csdn.net/young_gy/article/details/72633202
https://blog.csdn.net/u012759136/article/details/52302426
2. CS231n
http://cs231n.github.io/neural-networks-3/#hyper
3. 伪代码图片
https://blog.csdn.net/bvl10101111/article/details/72615436
4. Adam
https://segmentfault.com/a/1190000012668819
https://www.jianshu.com/p/3e363f5e1a79