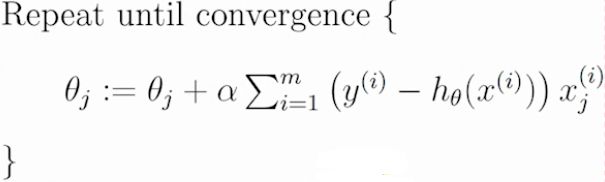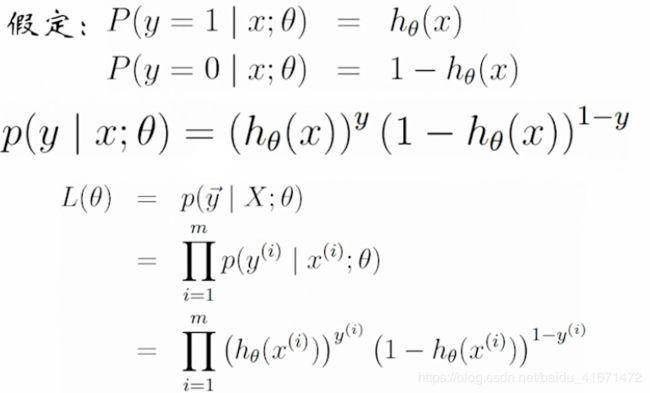瞎写一通

通过fuzzywuzzy进行模糊查询，通过提取相似度进行数据修正（city列名字可以有错）

#!/usr/bin/python
# -*- encoding: utf-8

import numpy as np
import pandas as pd
from fuzzywuzzy import fuzz
from fuzzywuzzy import process


def enum_row(row):
    print(row['state'])# 输出state列中的值


def find_state_code(row):
    if row['state'] != 0:
        print(process.extractOne(row['state'], states, score_cutoff=80))
        # 输出相似度大于80的，按顺序输出，不排序


def capital(str):
    return str.capitalize()


def correct_state(row):
    if row['state'] != 0:
        state = process.extractOne(row['state'], states, score_cutoff=80)# 提取最相似的值，且大于80的相似度
        if state:
            state_name = state[0]
            return ' '.join(map(capital, state_name.split(' ')))
    return row['state']


def fill_state_code(row):
    if row['state'] != 0:
        state = process.extractOne(row['state'], states, score_cutoff=80)
        if state:
            state_name = state[0]
            return state_to_code[state_name]
    return ''


if __name__ == "__main__":
    pd.set_option('display.width', 200) # set_option 函数仅用作显示设置，这里的dispaly.width 设置为200，表示一行最多显示200个字符
    pd.set_option('display.max_columns', 200) # 设置最多显示200列，而中间不用 ... 来代替
    data = pd.read_excel('./sales.xlsx', sheet_name='sheet1', header=0) # sheet_name 是 excle中哪个sheet
    print('data.head() = \n', data.head()) # data.head() 中 默认有5行数据（不算head）
    print('data.tail() = \n', data.tail()) # 默认输出后5行
    print('data.dtypes = \n', data.dtypes) # 表示列所对应的数据类型
    print('data.columns = \n', data.columns) # 可以转为一个列表，存储列的名字
    for c in data.columns:
        print(c, end=' ')
    print()
    data['total'] = data['Jan'] + data['Feb'] + data['Mar']
    # 把Jan，Feb，Mar三列的值加起来，加到新的total列中
    print(data.head())
    print(data['Jan'].sum()) # Jan列的总和
    print(data['Jan'].min()) # Jan列的最小值
    print(data['Jan'].max()) # Jan列的最大值
    print(data['Jan'].mean()) # Jan列的平均值

    print('=============')
    # 添加一行
    s1 = data[['Jan', 'Feb', 'Mar', 'total']].sum() # 直接求出Jan，Feb，Mar，total列的总和，返回一个列表
    print(s1)
    s2 = pd.DataFrame(data=s1)
    print(s2) # 将s1的值 输入到s2
    print(s2.T) # 将s2列表转制
    print(s2.T.reindex(columns=data.columns)) # 将s2与原数据通过columns进行合并
    # 即：
    s = pd.DataFrame(data=data[['Jan', 'Feb', 'Mar', 'total']].sum()).T
    s = s.reindex(columns=data.columns, fill_value=0) # 类似于上述的操作，这里的fill_value对于空值填充0
    print(s)
    data = data.append(s, ignore_index=True) # 把 上面合并的数据 添加到原数据的后一行
    # 所以上述操作就是 先分别求出 Jan,Feb,Mar三列的和，再在最后一行对应位置添加上其和
    data = data.rename(index={15:'Total'})
    print(data.tail())

    # apply的使用
    print('==============apply的使用==========')
    data.apply(enum_row, axis=1)
    # enum_row为自定义函数名，传入参数通过axis的值判断
    # axis = 1表示按行遍历，传入enum_row行值，=0表示按列进行遍历
    state_to_code = {"VERMONT": "VT", "GEORGIA": "GA", "IOWA": "IA", "Armed Forces Pacific": "AP", "GUAM": "GU",
                     "KANSAS": "KS", "FLORIDA": "FL", "AMERICAN SAMOA": "AS", "NORTH CAROLINA": "NC", "HAWAII": "HI",
                     "NEW YORK": "NY", "CALIFORNIA": "CA", "ALABAMA": "AL", "IDAHO": "ID",
                     "FEDERATED STATES OF MICRONESIA": "FM",
                     "Armed Forces Americas": "AA", "DELAWARE": "DE", "ALASKA": "AK", "ILLINOIS": "IL",
                     "Armed Forces Africa": "AE", "SOUTH DAKOTA": "SD", "CONNECTICUT": "CT", "MONTANA": "MT",
                     "MASSACHUSETTS": "MA",
                     "PUERTO RICO": "PR", "Armed Forces Canada": "AE", "NEW HAMPSHIRE": "NH", "MARYLAND": "MD",
                     "NEW MEXICO": "NM",
                     "MISSISSIPPI": "MS", "TENNESSEE": "TN", "PALAU": "PW", "COLORADO": "CO",
                     "Armed Forces Middle East": "AE",
                     "NEW JERSEY": "NJ", "UTAH": "UT", "MICHIGAN": "MI", "WEST VIRGINIA": "WV", "WASHINGTON": "WA",
                     "MINNESOTA": "MN", "OREGON": "OR", "VIRGINIA": "VA", "VIRGIN ISLANDS": "VI",
                     "MARSHALL ISLANDS": "MH",
                     "WYOMING": "WY", "OHIO": "OH", "SOUTH CAROLINA": "SC", "INDIANA": "IN", "NEVADA": "NV",
                     "LOUISIANA": "LA",
                     "NORTHERN MARIANA ISLANDS": "MP", "NEBRASKA": "NE", "ARIZONA": "AZ", "WISCONSIN": "WI",
                     "NORTH DAKOTA": "ND",
                     "Armed Forces Europe": "AE", "PENNSYLVANIA": "PA", "OKLAHOMA": "OK", "KENTUCKY": "KY",
                     "RHODE ISLAND": "RI",
                     "DISTRICT OF COLUMBIA": "DC", "ARKANSAS": "AR", "MISSOURI": "MO", "TEXAS": "TX", "MAINE": "ME"}
    states = list(state_to_code.keys()) # 上面字典的所有key值组成的列表
    print(fuzz.ratio('Python Package', 'PythonPackage'))
    # fuzz为模糊查询模块，ratio相似度
    # 任何一个字符串：增删插入都算一次编辑，A字符串到B字符串的最小编辑距离除以最大值得到相似度
    print(process.extract('Mississippi', states))
    # 输出 'Mississippi' 与states中所有值进行相似度比较
    print(process.extract('Mississipi', states, limit=1))
    # limit=1，只抽取相似度最高的那一个
    print(process.extractOne('Mississipi', states))
    # 要求只抽取相似度最高的那一个
    data.apply(find_state_code, axis=1)

    print('Before Correct State:\n', data['state'])
    data['state'] = data.apply(correct_state, axis=1)
    print('After Correct State:\n', data['state'])
    data.insert(5, 'State Code', np.nan)
    data['State Code'] = data.apply(fill_state_code, axis=1)
    print(data)

    # group by
    print('==============group by================')
    print(data.groupby('State Code'))
    print('All Columns:\n')
    print(data.groupby('State Code').sum())
    print('Short Columns:\n')
    print(data[['State Code', 'Jan', 'Feb', 'Mar', 'total']].groupby('State Code').sum())

    # 写入文件
    data.to_excel('sales_result.xls', sheet_name='Sheet1', index=False)

鸢尾花测试

5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5.0,3.6,1.4,0.2,Iris-setosa
5.4,3.9,1.7,0.4,Iris-setosa
4.6,3.4,1.4,0.3,Iris-setosa
5.0,3.4,1.5,0.2,Iris-setosa
4.4,2.9,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.4,3.7,1.5,0.2,Iris-setosa
4.8,3.4,1.6,0.2,Iris-setosa
4.8,3.0,1.4,0.1,Iris-setosa
4.3,3.0,1.1,0.1,Iris-setosa
5.8,4.0,1.2,0.2,Iris-setosa
5.7,4.4,1.5,0.4,Iris-setosa
5.4,3.9,1.3,0.4,Iris-setosa
5.1,3.5,1.4,0.3,Iris-setosa
5.7,3.8,1.7,0.3,Iris-setosa
5.1,3.8,1.5,0.3,Iris-setosa
5.4,3.4,1.7,0.2,Iris-setosa
5.1,3.7,1.5,0.4,Iris-setosa
4.6,3.6,1.0,0.2,Iris-setosa
5.1,3.3,1.7,0.5,Iris-setosa
4.8,3.4,1.9,0.2,Iris-setosa
5.0,3.0,1.6,0.2,Iris-setosa
5.0,3.4,1.6,0.4,Iris-setosa
5.2,3.5,1.5,0.2,Iris-setosa
5.2,3.4,1.4,0.2,Iris-setosa
4.7,3.2,1.6,0.2,Iris-setosa
4.8,3.1,1.6,0.2,Iris-setosa
5.4,3.4,1.5,0.4,Iris-setosa
5.2,4.1,1.5,0.1,Iris-setosa
5.5,4.2,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.0,3.2,1.2,0.2,Iris-setosa
5.5,3.5,1.3,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
4.4,3.0,1.3,0.2,Iris-setosa
5.1,3.4,1.5,0.2,Iris-setosa
5.0,3.5,1.3,0.3,Iris-setosa
4.5,2.3,1.3,0.3,Iris-setosa
4.4,3.2,1.3,0.2,Iris-setosa
5.0,3.5,1.6,0.6,Iris-setosa
5.1,3.8,1.9,0.4,Iris-setosa
4.8,3.0,1.4,0.3,Iris-setosa
5.1,3.8,1.6,0.2,Iris-setosa
4.6,3.2,1.4,0.2,Iris-setosa
5.3,3.7,1.5,0.2,Iris-setosa
5.0,3.3,1.4,0.2,Iris-setosa
7.0,3.2,4.7,1.4,Iris-versicolor
6.4,3.2,4.5,1.5,Iris-versicolor
6.9,3.1,4.9,1.5,Iris-versicolor
5.5,2.3,4.0,1.3,Iris-versicolor
6.5,2.8,4.6,1.5,Iris-versicolor
5.7,2.8,4.5,1.3,Iris-versicolor
6.3,3.3,4.7,1.6,Iris-versicolor
4.9,2.4,3.3,1.0,Iris-versicolor
6.6,2.9,4.6,1.3,Iris-versicolor
5.2,2.7,3.9,1.4,Iris-versicolor
5.0,2.0,3.5,1.0,Iris-versicolor
5.9,3.0,4.2,1.5,Iris-versicolor
6.0,2.2,4.0,1.0,Iris-versicolor
6.1,2.9,4.7,1.4,Iris-versicolor
5.6,2.9,3.6,1.3,Iris-versicolor
6.7,3.1,4.4,1.4,Iris-versicolor
5.6,3.0,4.5,1.5,Iris-versicolor
5.8,2.7,4.1,1.0,Iris-versicolor
6.2,2.2,4.5,1.5,Iris-versicolor
5.6,2.5,3.9,1.1,Iris-versicolor
5.9,3.2,4.8,1.8,Iris-versicolor
6.1,2.8,4.0,1.3,Iris-versicolor
6.3,2.5,4.9,1.5,Iris-versicolor
6.1,2.8,4.7,1.2,Iris-versicolor
6.4,2.9,4.3,1.3,Iris-versicolor
6.6,3.0,4.4,1.4,Iris-versicolor
6.8,2.8,4.8,1.4,Iris-versicolor
6.7,3.0,5.0,1.7,Iris-versicolor
6.0,2.9,4.5,1.5,Iris-versicolor
5.7,2.6,3.5,1.0,Iris-versicolor
5.5,2.4,3.8,1.1,Iris-versicolor
5.5,2.4,3.7,1.0,Iris-versicolor
5.8,2.7,3.9,1.2,Iris-versicolor
6.0,2.7,5.1,1.6,Iris-versicolor
5.4,3.0,4.5,1.5,Iris-versicolor
6.0,3.4,4.5,1.6,Iris-versicolor
6.7,3.1,4.7,1.5,Iris-versicolor
6.3,2.3,4.4,1.3,Iris-versicolor
5.6,3.0,4.1,1.3,Iris-versicolor
5.5,2.5,4.0,1.3,Iris-versicolor
5.5,2.6,4.4,1.2,Iris-versicolor
6.1,3.0,4.6,1.4,Iris-versicolor
5.8,2.6,4.0,1.2,Iris-versicolor
5.0,2.3,3.3,1.0,Iris-versicolor
5.6,2.7,4.2,1.3,Iris-versicolor
5.7,3.0,4.2,1.2,Iris-versicolor
5.7,2.9,4.2,1.3,Iris-versicolor
6.2,2.9,4.3,1.3,Iris-versicolor
5.1,2.5,3.0,1.1,Iris-versicolor
5.7,2.8,4.1,1.3,Iris-versicolor
6.3,3.3,6.0,2.5,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
7.1,3.0,5.9,2.1,Iris-virginica
6.3,2.9,5.6,1.8,Iris-virginica
6.5,3.0,5.8,2.2,Iris-virginica
7.6,3.0,6.6,2.1,Iris-virginica
4.9,2.5,4.5,1.7,Iris-virginica
7.3,2.9,6.3,1.8,Iris-virginica
6.7,2.5,5.8,1.8,Iris-virginica
7.2,3.6,6.1,2.5,Iris-virginica
6.5,3.2,5.1,2.0,Iris-virginica
6.4,2.7,5.3,1.9,Iris-virginica
6.8,3.0,5.5,2.1,Iris-virginica
5.7,2.5,5.0,2.0,Iris-virginica
5.8,2.8,5.1,2.4,Iris-virginica
6.4,3.2,5.3,2.3,Iris-virginica
6.5,3.0,5.5,1.8,Iris-virginica
7.7,3.8,6.7,2.2,Iris-virginica
7.7,2.6,6.9,2.3,Iris-virginica
6.0,2.2,5.0,1.5,Iris-virginica
6.9,3.2,5.7,2.3,Iris-virginica
5.6,2.8,4.9,2.0,Iris-virginica
7.7,2.8,6.7,2.0,Iris-virginica
6.3,2.7,4.9,1.8,Iris-virginica
6.7,3.3,5.7,2.1,Iris-virginica
7.2,3.2,6.0,1.8,Iris-virginica
6.2,2.8,4.8,1.8,Iris-virginica
6.1,3.0,4.9,1.8,Iris-virginica
6.4,2.8,5.6,2.1,Iris-virginica
7.2,3.0,5.8,1.6,Iris-virginica
7.4,2.8,6.1,1.9,Iris-virginica
7.9,3.8,6.4,2.0,Iris-virginica
6.4,2.8,5.6,2.2,Iris-virginica
6.3,2.8,5.1,1.5,Iris-virginica
6.1,2.6,5.6,1.4,Iris-virginica
7.7,3.0,6.1,2.3,Iris-virginica
6.3,3.4,5.6,2.4,Iris-virginica
6.4,3.1,5.5,1.8,Iris-virginica
6.0,3.0,4.8,1.8,Iris-virginica
6.9,3.1,5.4,2.1,Iris-virginica
6.7,3.1,5.6,2.4,Iris-virginica
6.9,3.1,5.1,2.3,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
6.8,3.2,5.9,2.3,Iris-virginica
6.7,3.3,5.7,2.5,Iris-virginica
6.7,3.0,5.2,2.3,Iris-virginica
6.3,2.5,5.0,1.9,Iris-virginica
6.5,3.0,5.2,2.0,Iris-virginica
6.2,3.4,5.4,2.3,Iris-virginica
5.9,3.0,5.1,1.8,Iris-virginica

• 前4列：‘花萼长度’, ‘花萼宽度’, ‘花瓣长度’, ‘花瓣宽度’，第5列：花的’类型’
• 通过三种类别的花，训练一个机器学习的模型来识别花是什么类型的花
• y = X
• X={‘花萼长度’, ‘花萼宽度’, ‘花瓣长度’, ‘花瓣宽度’},y={花的’类型’}
• 通过X的取值，去判断y的值
• 一般X往往是向量，y一般是标量

假设

• 机器学习需要假设
• 假设具有内涵性，简化性，发散性
• 内涵性：
  • 根据常理应该是正确的
  • 假定成年人的身高在140～220之间
  • 假设往往是正确的，但不是完全正确的
• 简化性：
  • 不能够完全反应现实情况
  • 是一个现实上的简化
• 发散性：
  • 有的时候条件成立，结论成立
  • 有的时候条件不成立，结论成立
  • 有的时候条件成立，结论不成立

https://www.cnblogs.com/lliuye/p/9486500.html

线性回归

• 有监督学习：

  • 回归：y值往往是 身高，温度，价格等 连续值
  • 分类：y值往往是 离散值和类别

• 举个例子：

  • 身高高的人的后代，身高往往也比较高，但不至于比父辈高，所以越往后走身高逐渐降低到一个固定值附近
  • 身高矮的人的后代，身高往往比父辈高，所以子代身高会逐渐变高，也趋近于一个固定值附近
  • 最后大家都会在某个平均值附近回归

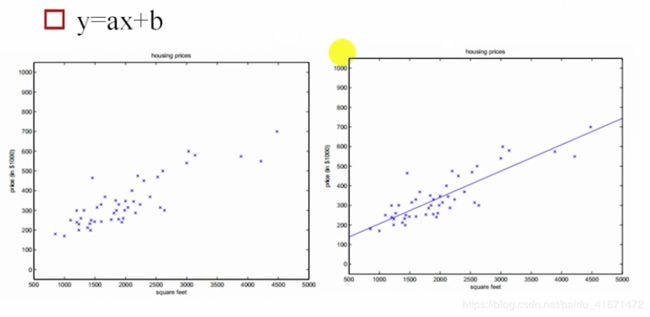
• 使线尽量的与所有点都接近，这里x轴代表房屋面积，y轴代表价格
• 当然，x作为条件可能不止一个（可能还有 x2 = 房间数，x3 = 是否有电梯等）
• 即：y = kx+b（一根线）
• 也可以是：y = k1 * x1 + k2 * x2 + k0（一个平面）
• 也可以是：$y={\sum }_{i=0}^{n}ki\ast Xi+k0$（n维）
• $K=\left\{\begin{array}{c}k0\\ k1\\ k2\\ k3\\ k4\\ ...\end{array}\right\}$ ，$X=\left\{\begin{array}{c}1\\ X1\\ X2\\ X3\\ X4\\ ...\end{array}\right\}$，则y=$K^T\ast X$
• 参数x1，x2…是已知的，k1，k2…是未知的

---

• 设$y^{(i)}=K^T{X}^{(i)}+{\epsilon }^{(i)}$

  • 其中 $X^{(i)}$表示第i个样本
  • $y^{(i)}$表示第i个样本计算出来的值
  • ${\epsilon }^{(i)}$表示第i个样本的与真实值$y$的误差

• 误差 ${\epsilon }^{(i)}$是独立同分布的，服从均值为0，方差为某定值${\sigma }^2$的高斯分布

  • 原因：中心极限原理

• 既然${\epsilon }^{(i)}$服从高斯分布，则将${\epsilon }^{(i)}=y^{(i)}-K^T{X}^{(i)}$带入高斯方程，就可以不去算${\epsilon }^{(i)}$

• 因为$\left\{y1,y2,y3...\right\}$是相互独立的，所以$y1\ast y2\ast y3...$的联合概率$L(y)$等于$p^{(y^{(i)}|X^{(i)};K)}$的乘积，就是似然函数

• 因为$x^{(i)}$$y^{(i)}$已知，所以是关于K的等式（这里的K和下图的$\Theta$同义）
  

• 两边去对数，得到对数似然

• m为定值，$\sigma$可以不用管是未知的某个定值，$x^{(i)}$$y^{(i)}$已知
• 要想$\iota (\Theta )$值越大，就是要$J(\Theta )$值越小

数据使用

• 将数据分为n份，其中n-1份做训练，1份做验证
• 则共有n种选取方式，最后能让每个数据即参与训练，又参与验证

梯度下降算法

• 使用梯度下降算法求解$J(\Theta )=1/2\ast {\sum }_{i=1}^m(h_{\Theta }(X^{(i)}-y^{(i)}){)}^2$
• 初始化$\Theta$（随机初始化）
• 沿着负梯度方向迭代，更新后的$\Theta$使$J(\Theta )$更小$\Theta =\Theta -\alpha \ast \partial \ast J(\Theta )/\partial \Theta$
  • 其中$\alpha$为：学习率，步长
• 从某个点开始，往其四周向下的点迭代，直到找到到一个局部最小值

批量梯度下降算法

• 沿着所有样本样本的梯度下降

• 随机梯度下降算法（用的更多，下降更快，迭代时间更短）

  • 拿到第i个样本，就下降一次
  • 拿到就下降
    

• 折中：mini-batch

  • 不是每拿到一个样本就更改梯度，而是若干个样本的平均梯度作为更新方向
  • 例如：共1000个样本，分成20份，每份50个数据，也就是说每50个数据算一次梯度下降方向

Logistic回归

• Logistic/Sigmoid函数

# coding = utf-8

import matplotlib.pyplot as plt
import numpy as np


if __name__ == "__main__":
    np.set_printoptions(suppress=True)
    x = np.linspace(-7, 7, 101) # 从-7到7，总共生成101个数
    y = 1 / (1 + np.exp(-x))
    plt.plot(x, y, 'r-', lw=3) # red的线
    plt.show()
    pass

$g(z)=\frac{1}{1+e^{-z}}$

• 上图是一个形似S的曲线，所以叫它Sigmoid函数
• 将$z$换成$\Theta X$，其中$\Theta X$就是线性回归模型
• 替换后$h_{\Theta }=g({\Theta }^{T}X)=\frac{1}{1+e^{-{\Theta }^{T}x}}$
• $g^{\prime }(x)={\left\{\frac{1}{1+e^{-x}}\right\}}^{\prime }=\frac{e^{-x}}{(1+e^{-x}{)}^2}=g(x)\ast (1-g(x))$

• 再求对数似然函数
  

决策树和随机森林

• 随机森林由多个决策树构成
• 理论上，能够构建一个决策树就能构建出一个随机森林

熵

• 对随机事件信息量求期望，得熵的定义：$H(X)=-{\sum }_{x\in X}p(x)lnp(x)$
  • 经典熵的定义，底数是2，单位是bit
  • 为方便分析，底数使用$e$，若底数

举个例子
$H(X)=-lnP(X)$

1. $P(X)=0.9999$ X(例如：国乒夺冠)发生，带来的信息量$Hx$
2. $P(Y)=0.3000$ Y(例如：女排夺冠)发生，带来的信息量$Hy$
3. $P(Z)=0.00001$ Z(例如：国足出线)发生，带来的信息量$Hz$

• 上述信息量和出现的概率就是相反的

---

X	1	2	3	4	…
P	$p^{(1)}$	$p^{(2)}$	$p^{(3)}$	$p^{(4)}$	…
-lnP	$-ln{p}^{(1)}$	$-ln{p}^{(2)}$	$-ln{p}^{(3)}$	$-ln{p}^{(4)}$	…

• 随机事件X
• 他的信息量$H(X)$是${\sum }_{i=1}^n{p}^{(i)}\ast ln{p}^{(i)}$

分析一下$H(X)的两点分布$

X	0	1
P	1-p	p

• 通过上面的公式得
• $H(p)=-(1-p)\ast ln(1-p)-plnp$，这里因为$H(p)$是关于$p$的函数，所以将$H(X)$换成$H(p)$

import matplotlib.pyplot as plt
import numpy as np


if __name__ == "__main__":
    np.set_printoptions(suppress=True)
    p = np.linspace(0, 1, 100)
    h = -(1-p)*np.log(1-p) - p*np.log(p)
    plt.plot(p, h, 'ro', lw=3)
    plt.show()
    pass

• 从上面的编码图片可以看出，如果X要么等于0要么等于1，则随机事件几乎退化成了确定性事件，它的信息熵为0
  • ‘太阳明天从东方升起’，人尽皆知，是句废话，带来的信息熵为0
  • ‘太阳明天从西方升起’，几乎不可能，是句废话，带来的信息熵为0

决策树

• 从熵的解释，可以这么理解，如果某个特征能使子节点的熵下降的更快，那么就选择哪个特征，这种决定可以让决策树更有效

tensorflow

前向传播

#coding=utf-8

# 两层简单神经网络
import tensorflow as tf

# 定义输入和参数
x = tf.constant([[0.7, 0.5]]) # 定义x，这里表示一个 一行 两列的 二维张量
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))# 正太分布随机出 2行 3列的矩阵，标准差为1，随机种子为1
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))# 正太分布随机出 3行 1列的矩阵，标准差为1，随机种子为1

# 定义前向传播的传播过程
a = tf.matmul(x, w1) # matmul 矩阵乘法
y = tf.matmul(a, w2) # 这里仅仅只是定义 而没有进行实际运算

# 使用with结构进行运算
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    print(sess.run(y))

#coding=utf-8

# 两层简单神经网络
import tensorflow as tf

# 定义输入和参数
x = tf.placeholder(tf.float32, shape=(1, 2)) # 定义x的输入格式，float32类型，1行 2列
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))# 正太分布随机出 2行 3列的矩阵，标准差为1，随机种子为1
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))# 正太分布随机出 3行 1列的矩阵，标准差为1，随机种子为1

# 定义前向传播的传播过程
a = tf.matmul(x, w1) # matmul 矩阵乘法
y = tf.matmul(a, w2) # 这里仅仅只是定义 而没有进行实际运算

# 使用with结构进行运算
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    print(sess.run(y. feed_dict={x:[[0.7, 0.5]]}))# 在这里传入x的参数

import tensorflow as tf

# 定义输入和参数
x = tf.placeholder(tf.float32, shape=(None, 2)) # 定义x的输入格式，float32类型，2列，因为不知道多少组 所以使用None来 占位
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))# 正太分布随机出 2行 3列的矩阵，标准差为1，随机种子为1
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))# 正太分布随机出 3行 1列的矩阵，标准差为1，随机种子为1

# 定义前向传播的传播过程
a = tf.matmul(x, w1) # matmul 矩阵乘法
y = tf.matmul(a, w2) # 这里仅仅只是定义 而没有进行实际运算

# 使用with结构进行运算
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    print(sess.run(y, feed_dict={x:[[0.7, 0.5],[0.2,0.3],[0.3,0.4],[0.4,0.5]]}))# 在这里传入x的参数

反向传播

#encoding=utf-8

import tensorflow as tf
import numpy as np

BATCH_SIZE = 8 # 一次喂入神经网路网络的数据,太多为导致不容易运行出来
seed = 23455 # 设置随机种子，保证每次运行时随机出来的值都一样

# 基于sedd产生随机值

rng = np.random.RandomState(seed)

# 随机数返回32行2列的矩阵，表示32组 体积shell质量 作为输入数据集、
X = rng.rand(32, 2)

# 从X这个32行2列的矩阵中 取出一行 判断如果小于1 则给Y赋值1 和不小于一则赋值0
# 这里相当于给Y分类，x0+x1 < 1是一类，另一个是另一类
Y = [[int(x0+x1 < 1)] for (x0, x1) in X]

print("X", X)
print("Y", Y)

# 定义神经网路的输入，参数和输出，定义钱箱传播过程
x = tf.placeholder(tf.float32, shape=(None, 2)) # x1 x2 作为一行 因为不知道有多少组，所以第一个参数为None
y_ = tf.placeholder(tf.float32, shape=(None, 1)) # y 作为类别，同理不知道多少组 所以第一个参数为None

w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1)) # 第一个参数2 对应于x的参数个数 隐藏层用3个神经元
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1)) # 第二个参数1 对应于y的参数个数 隐藏层用3个神经元
# stddev 是样本标准差
# 为保证吗 每次运行的时候随机值都一样 所以设置seed

a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

# 定义损失函数及反向传播方法
loss = tf.reduce_mean(tf.square(y-y_)) # 选用均衡误差来计算损失函数
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss) # 选用梯度下降实现训练过程，学习率是0,001
# 学习率：表示了每次更新参数的幅度大小。学习率过大，会导致待优化的参数在最小值附近波动，不收敛；学习率过小，会导致待优化的参数收敛缓慢。

# 生成会话 训练SETPS轮

with tf.Session() as sess:
    init_op = tf.global_variables_initializer() # 初始化所有变量
    sess.run(init_op)
    # 输出目前（未经训练）的参数取值
    print(sess.run(w1))
    print(sess.run(w2))

    # 训练模型
    STEPS = 3000
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 32
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]}) # 每次抽取start到end的数据喂入神经网络
        if(i%500) == 0: # 每500 轮打印一次loss值
            total_loss = sess.run(loss, feed_dict={x: X, y_: Y})
            print("after %d training step(s), loss on all data is %g_"%(i, total_loss))

    # 输出训练后的参数取值
    print("")
    print("w1", sess.run(w1))
    print("w2", sess.run(w2))

1. 前向传播：定义输入，参数和输出
   • 输入答案 x，输出答案 y
   • 第一层网络参数：w1，第二层网络参数：w2
   • 定义a，y推理过程
2. 反向传播：定义损失函数，反向传播方法
   • loss 损失函数
   • train_strp 反向传播方法
3. 生成会话，训练STRPS轮

激活函数

• NN复杂度：多用NN层数和NN参数的个数表示

  • 层数 = 隐藏层的层数+1个输出层
  • 总参数 = 总W + 总ｂ

• 损失函数loss：预测值（y）和已知答案（y_）的差距：

  • NN优化目标：loss最小
    1. mse（mean squraed error）：均方误差
    2. 自定义
    3. ce（Cross Entropy）：交叉熵

• 均方误差mse：$MSE(y\_,y)=(({\sum }_{i=1}^n(y-y\_{)}^2)/n)$

  • python表示 : loss_mse = tf.reduce_mean(tf.square(y_-y))

• 自定义损失函数：

  • loss = tf.reduce_sum(tf.where(tf.greater(y, y_), COST*(y - y_), PROFIT*(y_ - y)))
  • 上述式子的意思是：y > y_ ? cost*(y - y_) : profit*(y_ - y) 的一个 判断式子