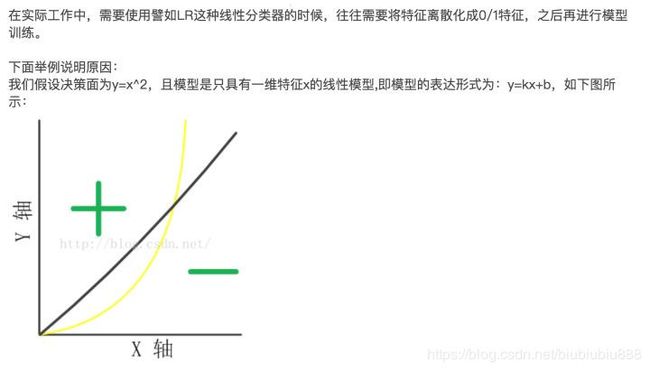
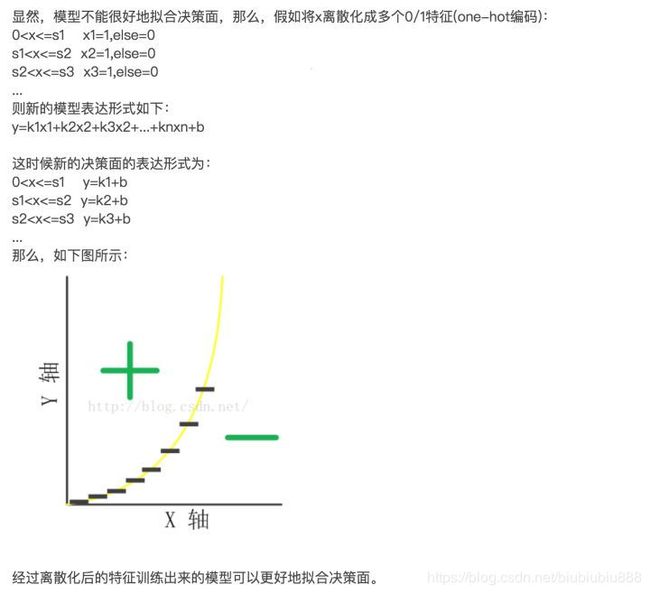
逻辑回归中的连续特征为什么要离散化处理？

LR面试题:

特征处理

LR并行化

 

特征处理

1.知乎上的一个问题:

https://www.zhihu.com/question/31989952

连续特征的离散化：在什么情况下将连续的特征离散化之后可以获得更好的效果？

题主机器学习大白一个。。最近刚接触CTR预估，发现CTR预估一般都是用LR，而且特征都是离散的。为什么一定要用离散特征呢？这样做的好处在哪里？求大拿们解答～
 

第一种解释:

在工业界，很少直接将连续值作为逻辑回归模型的特征输入，而是将连续特征离散化为一系列0、1特征交给逻辑回归模型，这样做的优势有以下几点：

0. 离散特征的增加和减少都很容易，易于模型的快速迭代；

1. 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；

2. 离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；

3. 逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；

4. 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；

5. 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；

6. 特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。

 

李沐曾经说过：模型是使用离散特征还是连续特征，其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型，也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。通常来说，前者容易，而且可以n个人一起并行做，有成功经验；后者目前看很赞，能走多远还须拭目以待。

评论理解:

. 假设目前有两个连续的特征：『年龄』和『收入』，预测用户的『魅力指数』；

1. 关于第三点指出，LR是广义线性模型，因此如果特征『年龄』不做离散化直接输入，那么只能得到『年龄』和魅力指数的一个线性关系。但是这种线性关系是不准确的，并非年龄越大魅力指一定越大；如果将年龄划分为M段，则可以针对每段有一个对应的权重；这种分段的能力为模型带来类似『折线』的能力，也就是所谓的非线性
2. 连续变量的划分，naive的可以通过人为先验知识划分，也可以通过训练单特征的决策树桩，根据Information Gain/Gini系数等来有监督的划分。
3. 假如『年龄』离散化后，共有N段，『收入』离散化后有M段；此时这两个离散化后的特征类似于CategoryFeature，对他们进行OneHotEncode，即可以得到 M + N的 01向量；例如： 0 1 0 0， 1 0 0 0 0；
4. 第四点中的特征交叉，可以理解为上述两个向量的互相作用，作用的方式可以例如是 &和|操作（这种交叉方式可以产生一个 M * N的01向量；）
5. 上面特征交叉，可以类比于决策树的决策过程。例如进行&操作后，得到一个1，则可以认为产生一个特征 （a < age < b && c < income < d）;将特征空间进行的非线性划分，也就是所谓的引入非线性；

第二种举例解释:

自己的感悟:

感觉第二种解释有点像CART做回归。

特征交叉

这个博客介绍的比较好。

https://blog.csdn.net/ccblogger/article/details/80180892

一．互联网广告特征工程

博文《互联网广告综述之点击率系统》论述了互联网广告的点击率系统，可以看到，其中的logistic regression模型是比较简单而且实用的，其训练方法虽然有多种，但目标是一致的，训练结果对效果的影响是比较大，但是训练方法本身，对效果的影响却不是决定性的，因为训练的是每个特征的权重，权重细微的差别不会引起ctr的巨大变化。
在训练方法确定后，对ctr预估起到决定性作用的是选用的特征。

 

1.1特征选择与使用

做点击率预估需要两方面的数据，一方面是广告的数据，另一方面是用户的数据，现在所有的数据都有，那么工作就是利用这两方面的数据评估用户点击这个广告的可能性（也就是概率）。
用户的特征是比较多的，用户的年龄，性别，地域，职业，学校，手机平台等等。广告的特征也很丰富，如广告大小，广告文本，广告所属行业，广告图片。还有反馈特征，如每个广告的实时ctr，广告跟性别交叉的ctr。如何从这么多的特征中选择到能刻画一个人对一个广告的兴趣的特征，是数据挖掘工程师的一个大难题。
选中了特征，还需要注意特征的选择方式，例如，如果单独把年龄作为一个特征，最终能训练出来啥吗？因为年龄相加相减是没有意义的，所以只能把每个年龄做为一个特征，但是光这样可以了吗？怎么用特征，是广告算法工程师的一个大课题。

1.1.1 选择特征

     什么样的特征适合用来预估ctr？这个问题是很多广告算法工程师的需要考虑的。
     机器学习算法最多会大谈模型，对于特征的讨论很少涉及。真正的应用中，多数数据挖掘工程师的工作都是在想特征，验证特征。
     想特征是一个脑力加体力的活，需要不少的领域的知识，更让人郁闷的是，工业界并没有一整套想特征的办法，工业界有的只是验证特征的办法。对于互联网广告业，就简单说说通用特征怎么来的吧。
首先说年龄这个特征，怎么知道它跟点击率有关系？现在直观的解释是，年轻人普遍喜欢运动类的广告，30岁左右的男人喜欢车，房子之类的广告，50岁以上的人喜欢保健品的广告。可以看到，选择年龄作为特征的理由是基于对各个年龄段的人喜欢的不同类型的东西的一个粗略的划分，是一个很主观的东西。
     再说性别这个特征，直观的感觉是，男性普遍喜欢体育类的，车类的，旅游类广告，女性普遍喜欢化妆品，服装类的广告。这也可以看到，选择性别作为特征也是基于相似的理由，就是认为男性和女性大体会喜欢不同的东西。
对于地域这个特征，这下就学问多了，华南的人在比较喜欢动漫和游戏，华北的人喜欢酒品和烟？
在广告方面的特征，广告的图片大小，广告前景色背景色真的能影响人的点击吗？这其实都是一种猜测。图片里面是一个明星还是一个动物之类的因素也可以考虑。

总结：选特征的流程，就是先猜想，然后统计验证，然后将特征加到模型中，进行验证。
总之，想特征的这个事情基本没多大谱，只能天南地北地想象，还要多了解各行各业的知识，以便想到更多的特征，哪怕某个特征跟人关系并不大，也得好好验证一番。 
想到了特征，就要验证和进行判断。
验证特征的办法多，有直接观察ctr，卡方检验，单特征AUC等。直接观察ctr是个很有效的方法，如根据投放记录，化妆品的广告在女性上面的点击率就比在男性上面的点击率高很多，说明性别这个特征在化妆品行业是有预测能力的；又如体育用品的广告在男性上面的点击率也比女性高，说明性别这个特征在体育行业也是有预测能力的，经过多个行业的验证，就认为性别这个特征可以用了。
年龄这个特征的评估类型，主要是观察一个广告在不同年龄段的点击率是否有区别，再观察不同广告的点击率在不同年龄段的分布是否不一样，如果都有区别，说明年龄这个特征就可以用了。
在实际的使用中发现，性别这个特征比较有效，手机平台这个特征也比较有效，地域和年龄这两个特征有一定效果，但没有前两个那么明显，跟他们的使用方式可能有关，还需要进一步挖掘。
同时，实际使用中也发现，广告反馈ctr这个特征也很有效，这个特征的意思就是当前的广告正在投放，已经投放了一部分了，这部分的点击率基本可以认为是这个广告的点击率了，也可以认为是这个广告的质量的一个体现，用来预估一个流量的ctr是很有效的。

1.1.2 特征的处理和使用

选择得到特征，怎么用也是一个问题。
先说需求，其实预估ctr要做的事情是下面的图的工作——计算一个用户/广告组合的ctr。

上面已经选好了特征，暂定有广告的反馈ctr，用户年龄，性别三个特征。
一、离散化，有些特征虽然也是数值型的，但是该特征的取值相加相减是没有实际意义的，那么该数值型特征也要看成离散特征，采用离散化的技术。
反馈ctr是一个浮点数，直接作为特征是可以的，假设1号特征就是反馈ctr。对应年龄来说就不是这样了，因为年龄不是浮点数，而且年龄的20岁跟30岁这两个数字20,30大小比较是没有意义的，相加相减都是没有意义的，在优化计算以及实际计算ctr是会涉及这两个数字的大小比较的。如w.x，在w已经确定的情况下，x的某个特征的值是20，或者30，w.x的值相差是很大的，哪怕用逻辑化公式再比较，得到的值也是比较大的，但是往往20岁的人跟30岁的人对同一个广告的兴趣差距不会那么大。解决这样的情况的方法就是，每个年龄一个特征，如总共只有20岁到29岁10种年龄，就把每个年龄做一个特征，编号是从2到11（1号是广告的反馈ctr），如果这个人是20岁，那么在编号为2的特征上的值就是1，3到11的编号上就是0。这样，年龄这一类特征就有了10个特征，而且这10个特征就是互斥的，这样的特征称为离散化特征。
二、交叉，交叉从理论上而言是为了引入特征之间的交互，也即为了引入非线性性。是有实际意义的。本文对交叉的意义解释得非常nice
这样看起来就能解决上面的问题了，但是够了吗？
比如一个人是20岁，那么在编号为2的特征上面，它一直都是1，对篮球的广告是1，对化妆品的广告也是1，这样训练的结果得到的编号为2的权重的意义是——20岁的人点击所有的广告的可能性的都是这个权重，这样其实是不合理的。
有意义的应该是，这个20岁的人，当广告是跟体育相关的时候，它是一个值；当广告跟保健品相关的时候，它又是一个值。这样看起来才合理。如果这个不够深刻，基于跟上面同样的道理，性别这个特征也是一样的，假如也做了上面的离散化操作，编号是12和13,12是男性，13是女性。这样的话，对于一个男性/体育广告组合来说，编号12的特征值为1，男性/化妆品的组合的编号12的特征值也是1。这样也是不合理的。
怎么做到合理呢？以上面的性别的例子来说。编号12的特征值不取1，取值为该广告在男性用户上面的点击率，如对于男性/体育广告的组合，编号12的特征的值为男性在体育广告上面点击率，这样，编号为12的特征就变成了一个浮点数，这个浮点数的相加减是有意义的。
这样的做法称为特征的交叉，现在就是性别跟广告的交叉得到的特征值。还有很多其他的方式可以进行交叉，目前工业上的应用最多的就是广告跟用户的交叉特征（编号为1的那个特征）、广告跟性别的交叉特征，广告跟年龄的交叉特征，广告跟手机平台的交叉特征，广告跟地域的交叉特征。如果做得比较多，可能会有广告主（每个广告都是一个广告主提交的一个投放计划，一个广告主可能会提交多个投放计划）跟各个特征的交叉。
三、连续特征变离散特征：连续特征离散化的基本假设，是默认连续特征不同区间的取值对结果的贡献是不一样的
做到的交叉的特征值就足够了吗？答案还是不一定。
如编号为1的那个特征，就是广告本身的ctr，假设互联网广告的点击率符合一个长尾分布，叫做对数正态分布，其概率密度是下图（注意这个是假设，不代表真实的数据，从真实的数据观察是符合这么样的一个形状的，好像还有雅虎的平滑的那个论文说它符合beta分布）。

可以看到，大部分广告的点击率都是在某一个不大的区间内的，点击率越高的广告越少，同时这些广告覆盖的流量也少。换句话说，点击率在0.2%左右的时候，如果广告a的点击率是0.2%，广告b的点击率是0.25%，广告b的点击率比广告a高0.05%，其实足以表示广告b比广a好不少,因为有足够多的样本支持这个结论；但是点击率在1.0%左右的的时候，广告a点击率是1.0%，广告b的点击率是1.05%，并没有办法表示广告b比广告a好很多，因为在这0.05%的区间内的广告并不多，两个广告基本可以认为差不多的。也就是点击率在不同的区间，应该考虑是不同的权重系数，因为这个由广告点击率组成的编号为1的特征与这个用户对广告的点击的概率不是完全的正相关性，有可能值越大特征越重要，也有可能值增长到了一定程度，重要性就下降了。比如说，在区间[0.2%,0.3%]区间的系数就要比[0.3%,0.4%]的系数大。故，我们如果将数值型特征进行区间离散化，就是默认不同区间的权重是不一样的。
对于这样的问题，百度有科学家提出了对连续特征进行离散化。他们认为，特征的连续值在不同的区间的重要性是不一样的，所以希望连续特征在不同的区间有不同的权重，实现的方法就是对特征进行划分区间，每个区间为一个新的特征。常用做法，就是先对特征进行排序，然后再按照等频离散化为N个区间
具体实现是使用等频离散化方式：1）对于上面的编号为1的那个特征，先统计历史记录中每条展示记录中编号为1的特征的值的排序，假设有10000条展示记录，每个展示记录的这个特征值是一个不相同的浮点数，对所有的展示记录按照这个浮点数从低到高排序，取最低的1000个展示记录的特征值作为一个区间，排名1001到2000的展示记录的特征值作为一个区间，以此类推，总共划分了10个区间。2）对特征编号重新编排，对于排名从1到1000的1000个展示记录，他们的原来编号为1的特征转变为新的特征编号1，值为1；对于排名是从1001到2000的记录，他们的原来编号为1的特征转变为新的特征编号2，值为1，以此类推，新的特征编号就有了1到10总共10个。对于每个展示记录来说，如果是排名1到1000的，新的特征编号就只有编号1的值为1，2到10的为0，其他的展示记录类似，这样，广告本身的ctr就占用了10个特征编号，就成为离散化成了10个特征。
等频离散化需要对原有的每个特征都做，也就是原来的编号为1到13的编号，会离散化成很多的编号，如果每个特征离散化成10个，则最终会有130个特征，训练的结果w就会是一个130维的向量，分别对应着130个特征的权重。
实际的应用表名，离散化的特征能拟合数据中的非线性关系，取得比原有的连续特征更好的效果，而且在线上应用时，无需做乘法运算，也加快了计算ctr的速度。

1.1.3 特征的过滤与修正

上面提到，很多特征其实是反馈的特征，如广告反馈ctr，广告与性别交叉特征，这些特征本来可以通过历史展示日志的统计得到。但有些广告本来展示量很少，在男性用户上展示就更少，这时要计算广告与性别交叉的ctr是很不准确的，需要对这个特征进行修正。具体的修正方法可以参考博文《广告点击率的贝叶斯平滑》。
经过修正后的ctr再做特征，实际线上效果有了比较大的提升。
如果使用的特征又更多了，有了学校跟广告交叉特征什么的，离散化后有了上万的特征，这下就会产生特征过多导致的各种问题，如过拟合等。解决这个问题的方法一种是离线的数据评估，如用ctr的区分性。另一种就是利用正则，特别是L1正则，经过L1正则训练的得到的权重向量，其中某些特征如果对点击率预估预测性不强，权重会变成0，不影响预估。这就是特征过滤，具体的有关L1的一些论述与实现参看博文《从广义线性模型到逻辑回归》《OWL-QN算法》和《在线学习算法FTRL》。

 

如何划分特征:

网上找的

连续特征离散化最常用的方法：

（1）划分区间

如1-100岁可以划分为：（0-18）未成年、（18-50）中青年、（50-100）中老年.

这其中包括等距划分、按阶段划分、特殊点划分等。

（2）卡方检验（CHI）

分裂方法，就是找到一个分裂点看，左右2个区间，在目标值上分布是否有显著差异，有显著差异就分裂，否则就忽略。这个点可以每次找差异最大的点。合并类似，先划分如果很小单元区间，按顺序合并在目标值上分布不显著的相邻区间，直到收敛。卡方值通常由χ2分布近似求得。

χ2表示观察值与理论值之问的偏离程度。计算这种偏离程度的基本思路如下：

(1)设A代表某个类别的观察频数，E代表基于H0计算出的期望频数，A与E之差称为残差。

(2)显然，残差可以表示某一个类别观察值和理论值的偏离程度，但如果将残差简单相加以表示各类别观察频数与期望频数的差别，则有一定的不足之处。因为残差有正有负，相加后会彼此抵消，总和仍然为0，为此可以将残差平方后求和。

(3)另一方面，残差大小是一个相对的概念，相对于期望频数为10时，期望频数为20的残差非常大，但相对于期望频数为1 000时20的残差就很小了。考虑到这一点，人们又将残差平方除以期望频数再求和，以估计观察频数与期望频数的差别。

进行上述操作之后，就得到了常用的χ2统计量，由于它最初是由英国统计学家Karl Pearson在1900年首次提出的，因此也称之为Pearson χ2，其计算公式为

　　(i=1，2，3，…，k)

当n比较大时，χ2统计量近似服从k-1(计算Ei时用到的参数个数)个自由度的卡方分布。

（3）信息增益法与信息增益比

 

LR并行化

 

2. 并行LR的实现

 

    由逻辑回归问题的求解方法中可以看出，无论是梯度下降法、牛顿法、拟牛顿法，计算梯度都是其最基本的步骤，并且L-BFGS通过两步循环计算牛顿方向的方法，避免了计算海森矩阵。因此逻辑回归的并行化最主要的就是对目标函数梯度计算的并行化。从公式(2)中可以看出，目标函数的梯度向量计算中只需要进行向量间的点乘和相加，可以很容易将每个迭代过程拆分成相互独立的计算步骤，由不同的节点进行独立计算，然后归并计算结果。

 

    将M个样本的标签构成一个M维的标签向量，M个N维特征向量构成一个M*N的样本矩阵，如图3所示。其中特征矩阵每一行为一个特征向量（M行），列为特征维度（N列）。

图3 样本标签向量 & 样本矩阵

 

    如果将样本矩阵按行划分，将样本特征向量分布到不同的计算节点，由各计算节点完成自己所负责样本的点乘与求和计算，然后将计算结果进行归并，则实现了“按行并行的LR”。按行并行的LR解决了样本数量的问题，但是实际情况中会存在针对高维特征向量进行逻辑回归的场景（如广告系统中的特征维度高达上亿），仅仅按行进行并行处理，无法满足这类场景的需求，因此还需要按列将高维的特征向量拆分成若干小的向量进行求解。

 

    (1) 数据分割

 

    假设所有计算节点排列成m行n列（m*n个计算节点），按行将样本进行划分，每个计算节点分配M/m个样本特征向量和分类标签；按列对特征向量进行切分，每个节点上的特征向量分配N/n维特征。如图4所示，同一样本的特征对应节点的行号相同，不同样本相同维度的特征对应节点的列号相同。

图4 并行LR中的数据分割

 

     一个样本的特征向量被拆分到同一行不同列的节点中，即：

其中Xr,k表示第r行的第k个向量，X(r,c),k表示Xr,k在第c列节点上的分量。同样的，用Wc表示特征向量W在第c列节点上的分量，即：

 

    (2) 并行计算

 

    观察目标函数的梯度计算公式(公式(2)),其依赖于两个计算结果：特征权重向量Wt和特征向量Xj的点乘，标量和特征向量Xj的相乘。可以将目标函数的梯度计算分成两个并行化计算步骤和两个结果归并步骤：

     ① 各节点并行计算点乘，计算，其中k=1,2,…,M/m，表示第t次迭代中节点(r,c)上的第k个特征向量与特征权重分量的点乘，Wc,t为第t次迭代中特征权重向量在第c列节点上的分量。

     ② 对行号相同的节点归并点乘结果：

计算得到的点乘结果需要返回到该行所有计算节点中，如图5所示。

图5 点乘结果归并

    ③ 各节点独立算标量与特征向量相乘：

G(r,c),t可以理解为由第r行节点上部分样本计算出的目标函数梯度向量在第c列节点上的分量。

     ④ 对列号相同的节点进行归并：

Gc,t就是目标函数的梯度向量Gt在第c列节点上的分量，对其进行归并得到目标函数的梯度向量：

这个过程如图6所示。

图6 梯度计算结果归并

 

    综合上述步骤，并行LR的计算流程如图7所示。比较图2和图7，并行LR实际上就是在求解损失函数最优解的过程中，针对寻找损失函数下降方向中的梯度方向计算作了并行化处理，而在利用梯度确定下降方向的过程中也可以采用并行化（如L-BFGS中的两步循环法求牛顿方向）。

图7 并行LR计算流程

 

3. 实验及结果

 

    利用MPI，分别基于梯度下降法（MPI_GD）和L-BFGS（MPI_L-BFGS）实现并行LR，以Liblinear为基准，比较三种方法的训练效率。Liblinear是一个开源库，其中包括了基于TRON的LR（Liblinear的开发者Chih-Jen Lin于1999年创建了TRON方法，并且在论文中展示单机情况下TRON比L-BFGS效率更高）。由于Liblinear并没有实现并行化（事实上是可以加以改造的），实验在单机上进行，MPI_GD和MPI_L-BFGS均采用10个进程。

 

    实验数据是200万条训练样本，特征向量的维度为2000，正负样本的比例为3:7。采用十折交叉法比较MPI_GD、MPI_L-BFGS以及Liblinear的分类效果。结果如图8所示，三者几乎没有区别。

图8 分类效果对比

 

    将训练数据由10万逐渐增加到200万，比较三种方法的训练耗时，结果如图9，MPI_GD由于收敛速度慢，尽管采用10个进程，单机上的表现依旧弱于Liblinear，基本上都需要30轮左右的迭代才能达到收敛；MPI_L-BFGS则只需要3~5轮迭代即可收敛（与Liblinear接近），虽然每轮迭代需要额外的开销计算牛顿方向，其收敛速度也要远远快于MPI_GD，另外由于采用多进程并行处理，耗时也远低于Liblinear。

图9 训练耗时对比