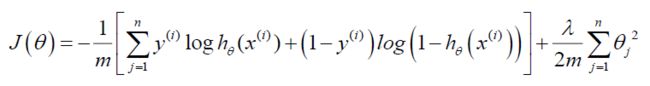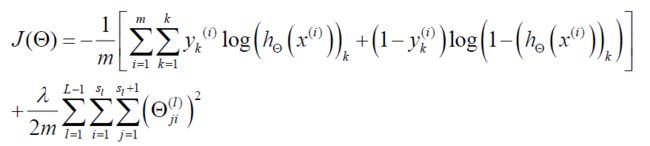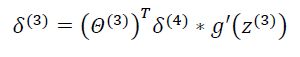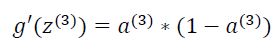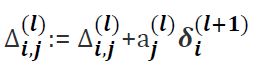吴恩达机器学习笔记之神经网络参数的反向传播算法

代价函数：

回顾Logistic Regression中的代价函数为：

神经网络的代价函数的基本思想与逻辑回归是一样的，但是形式上有一些差别：

L表示神经网络的层数，sl表示l层神经网中的神经元的个数，K表示输出层的神经元的个数；正则项的计算包含了每一个激活单元。

反向传播算法：

为了计算代价函数的偏导数，我们需要采用一种反向传播算法，它的目的是为了最小化我们的代价函数，即先计算最后一层的误差，然后在向前一层一层的计算，假如我们的神经网络有四层，并且输出单元有四个，那么最后一层的误差为： 

第三层的误差为：，其中，，类似的，

第二层的误差为：

注意：第一层是没有误差的，因为第一层是输入层，输入的是原始数据。

因此，我们不做任何正则化处理的代价函数的偏导数为：

l代表神经网络的层数，j代表目前计算层中激活单元的下标，i代表下一层中误差单元的下标。

我们用表示第j层神经网络中第i个激活单元受到第j个参数影响而导致的误差。△是的大写形式。

 一种向量化的实现方式：

j=0代表偏置单元，并不需要正则化。

我们如果用fminunc这样的优化算法求解权重矩阵的话，我们需要将矩阵首先展开成向量，在利用算法求出最优解后再重新转换成矩阵。假设有三个权重矩阵，Theta1，Theta2和Theta3，尺寸分别为10*11,10*11，和1*11，下面代码可以实现转换

代码实现：

thetaVec = [Theta1(:), Theta(:), Theta3(:)]
...optimization using function like fminunc...
Theta1 = reshape(thetaVec(1:110, 10, 11)); %取thetaVec的第1到110列，构成一个10*11的矩阵
Theta2 = reshape(thetaVec(111:220, 10, 11));
Theta3 = reshape(thetaVec(221:231, 1, 11));

反向传播的直观理解：

展开参数：

为了使用一些高级优化算法，比如fminunc，我们需要将参数从矩阵展成向量。

梯度检验：

单侧差分和双侧差分，双侧差分通常能得到更好的结果。

梯度检验的目的是检测我们的反向传播算法是否正常工作。

因为梯度其实就是该点切线的斜率，因此有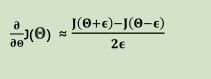：，所以对于多参数的矩阵来说也有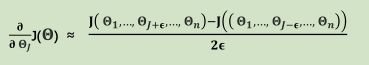：，我们的经典取值为。

MATLAB代码实现：

epsilon = 1e-4;
for i = 1:n,
    thetaPlus = theta;
    thetaPlus(i) += epsilon;
    thetaMinus = theta;
    thetaMinus(i) -= epsilon;
    gradApprox(i) = (J(thetaPlus) - J(thetaMinus)) / (2 * epsilon)
end;

然后检测gradApprox是不是和deltaVector近似相等，一旦你确信你的反向传播算法没有错误之后，你就应该关闭计算gradApprox，也就是梯度检验的算法，因为计算gradApprox的算法运算量很大，特别是如果你在循环里面加了这个检查算法的话，那么你的程序会跑的很慢。

随机初始化：

对称权重问题。在神经网络中，关于theta的初始化问题：在逻辑回归中，我们一般将theta初始化为全0矩阵，但是在神经网络中这样是不行的，因为这样会让下一层的神经网络中的所有神经元都进行着相同的运算，这是没有意义的,同理，全部初始化为相同的值也是没有用的。

因此我们采取对theta进行随机初始化的办法，通常采用的初始参数为正负之间的随机数，值得注意的是，这里的和前面梯度检验的没有关系，并不是同一个值。

代码实现：

...if the dimensions of Theta1 is 10*11...
Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
 %rand(m,n)表示随机产生一个m*n维的矩阵，且值都在0-1之间。

组合到一起：

第一步，选取神经网络的结构，有两个默认法则，第一个是默认只有一个隐藏层，第二个是如果有多个隐藏层，那么每个隐藏层之间的隐藏单元的数目应该一致。

隐藏单元一般来说越多越好，但是隐藏单元越多计算量也就越大。

网络结构：第一件要做的事是选择网络结构，即决定选择多少层以及决定每层分别有多
少个单元。
第一层的单元数即我们训练集的特征数量。
最后一层的单元数是我们训练集的结果的类的数量。
如果隐藏层数大于 1，确保每个隐藏层的单元个数相同，通常情况下隐藏层单元的个数
越多越好。
我们真正要决定的是隐藏层的层数和每个中间层的单元数。
训练神经网络：
1.  参数的随机初始化
2.  利用正向传播方法计算所有的
3.  编写计算代价函数 J 的代码
4.  利用反向传播方法计算所有偏导数
5.  利用数值检验方法检验这些偏导数
6.  使用优化算法来最小化代价函数