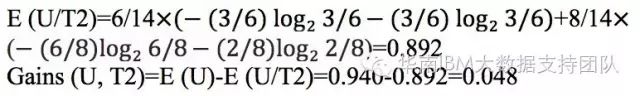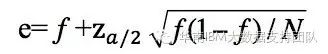IBM SPSS Modeler算法系列-----决策树C5.0算法
在之前的文章《IBM SPSS Modeler算法系列-----决策树CHAID算法》,我们介绍是CHAID算法,今天我们介绍另外一种用得非常广泛的决策树算法C5.0,该算法是专属于RuleQuest 研究有限公司(http://www.rulequest.com/)。
对于决策树算法来说,核心技术就是如何确定最佳分组变量和分割点,上次我们介绍的CHAID是以卡方检验为标准,而今天我们要介绍的C5.0则是以信息增益率作为标准,所以首先我们来了解下信息增益(Gains),要了解信息增益(Gains),先要明白信息熵的概念。
信息熵是信息论中的基本概念,信息论是1948年由C.E.Shannon提出并发展起来的,主要用于解决信息传递中的问题,也称统计通信理论。这些技术的概念很多书籍或者百度一下都有具体的介绍,我们这里不再赘述,我们通过一个例子来理解信息量和信息熵。
在拳击比赛中,两位对手谁能获得胜利,在对两位选择的实力没有任何了解的情况下,双方取得胜利的概率都是1/2,所以谁获得胜利这条信息的信息量,我们通过公式计算 :
其中p是每种情况出现的概率,这里计算出来的1bit就是谁获得胜利这条信息的信息量。如果信息是最后进入四强的选手谁获得最终胜利,它的信息量是 :
对比这个例子可以看到,不确定性越高,信息量就越大。
信息熵是信息量的数学期望,数学期望听起来有点陌生,但均值我相信大家都明白,那么在概率论和统计学中,数学期望指的就是均值,它是试验中每次可能出现的结果的概率乘以其结果的总和,它反映随机变量平均取值的大小。信息熵是平均信息量,也可以理解为不确定性。因此,信息熵的计算公式是:
仍以前面拳击比赛为例子,如果两对对手获胜的概率都为50%,那么信息熵:
如果两位对手A和B,根据以往的比赛历史经验判断,A胜利的概率是80%,B胜利的概率是20%,那么信息熵 :
对比以上结果,可以看到,经验减少了判断所需的信息量,消除了不确定性,A胜利的概率越高,计算出的信息熵就越小,也就是说,越是确定的事情,信息熵就越小。
理解了信息熵之后,我们回到C5.0这个算法,前面讲到, 确定该决策树最佳分组变量和分割点标准是信息增益率,我们通过例子来理解信息增益的内容。
还是以上面的例子,比赛胜利与失败是结果,那么影响这个结果的会有很多因素,这些因素是用来帮助我们判断结果的依据,一般会消除不确定性,那么消除不确定性的程度就是信息增益。
如下图:我们判断选择是否获胜的影响因素有选手类型T1(这里的类型分别为A攻击型、B综合型、C防守型)和是否单身T2(1表示非单身,0表示单身),我们收集到的数据如下:
在没有影响因素的时候,直接对结果是胜利还是失败的判断,这个信息熵我们称为初始熵,当加入了影响因素,或者是说增加了一些辅判断的信息,这时的信息熵我们称为后验熵,信息增益就是初始熵减去后验熵得到的结果,它反映的是消除不确定性的程度。计算公式如下:
Gains(U,T)=E(U)-E(U/T)
E(U)是初始熵,也就是是否获胜这个结果的信息熵,我们用公式计算
这个公式不难理解,上表中一共14条记录,9条结果是Y,5条结果N,也就是说,Y的概率是9/14,N的概率是5/14,信息量分别是:
和
信息熵就是每次可能结果的概率乘以其结果的总和,所以得到上面的计算结果。
E(U/T)是后验熵,我们先以T1为例,T1有三种结果,分别是A、B、C,每一个的概率分别是5/14,4/14,5/14。
在A这一类型里面,一共有5条记录,其中结果为Y的概率是2/5,结果为N的是3/5。因此获取结果为A的信息熵为
同理,
B类型的信息熵为:
C类型的信息熵为:
因此
而信息增益Gains(U,T1)=E(U)-E(U/T1)=0.940-0.694=0.246
接下来,对T2进行信息增益的计算,得到的结果为:
通过计算可以看到Gains(U,T1)>Gains(U,T2),因此,应该选择信息增益最大的输入变量T1作为最佳分组变量,因为它消除的不确定性程度最大,换句话说,就是因为有了T1这个信息,要确定结果是胜利与否的把握程度要比T2这个信息更高了。
可能,有人会注意到,计算信息增益Gains的时候,类别的值越多,计算得到的Gains值就越大,这会使得类别元素多的指标有天然优势成为分割节点,因此在C5.0算法中,不是直接使用信息增益,而是使用信息增益率来作为分割标准。
所以,信息增益率:
同理
因此,GainsR(U,T1)> GainsR(U,T2),还是要选择T1作为当前最佳分组变量。
那么以上是针对分类变量的情况,如果是数值变量,那跟我们之前文章讲到的CHAID算法一样,对数值变量进行离散化成为区间,在C5.0里面,使用的是MDLP的熵分箱方法 (还记得吗?CHAID使用的是ChiMerge分组方法),MDLP全称是“MinimalDescription Length Principle”,即最短描述长度原则的熵分箱法。基于MDLP的熵分箱的核心测度指标是信息熵和信息增益。
MDLP分箱法,计算步骤如下:
· Step1:首先也是对连续变量作排序;
· Step2:取两相邻值的平均作为分割点的值,分别计算每个分割点的信息增益, 取信息增益最大的分割点作为第一个分割点。
· Step3:第一个分割点确定后,分为两组,针对第一组和第二组,分别重复Step2,确定下一个分割点。
· Step4:停止条件:当每一组计算得到的最大信息增益值小于标准时,就无需再继续下去,即确定的分割点,必须满足:
在决策树生长完成之后,为了避免它过于“依赖”训练样本出现过度拟合的问题,需要对树进行剪枝,C5.0采用后修剪方法从叶节点向上逐层剪枝,其关键的技术点是误差估计以及剪枝标准的设置。C5.0使用了统计的置信区间的估计方法,直接在Training Data中估计误差。
估计误差使用的公式如下:
f为观察到的误差率(其中E为N个实例中分类错误的个数)
e为真实的误差率,a为置信度( 默认值为0.25),z为对应于置信度a的标准差,其值可根据a的设定值通过查正态分布表得到(这里a=0.25,对应的Za/2=1.15)。通过该公式即可计算出真实误差率e的一个置信度上限,用此上限为该节点误差率e做一个悲观的估计。
计算了每个分支节点的误差估计之后,按“减少-误差(Reduce-Error)”法判断是否剪枝。首先,计算待剪子树中叶节点的加权误差;然后与父节点的误差进行比较,如果计算待剪子树中叶节点的加权误差大于父节点的误差,则可以剪掉,否则不能剪掉。
这里值得注意的是,C5.0算法只支持分类变量作为目标,不支持连续变量作为目标。
在C5.0算法里面,它的独特之处是,除了构建决策树,还能够生成推理规则集,它的一般算法是PRISM(Patient Rule Introduction Space Method),它所生成的规则集跟其它决策树算法生成的规则集原理并不一样,其它决策树生成的规则集是根据决策树生长结果,得到的规则,如下图(以C5.0生成决策树为例):
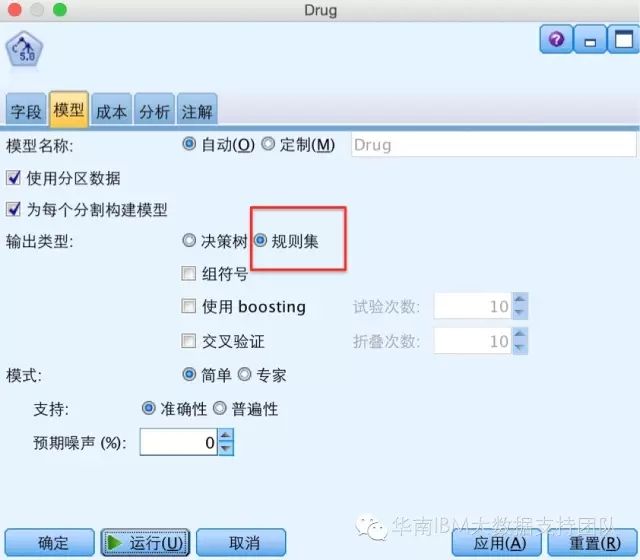
而C5.0里面构建规则集,是在生成模型之前就可以选择”规则集”
然后生成的模型结果就不是树状图,而是以下的规则内容:
那么对于C5.0算法中,生成推理规则算法PRISM的具体计算逻辑,感兴趣的朋友可以给我们留言,我们下次再做具体介绍。
如果想进一步了解,可以点击下面的链接下载试用版了解!
http://bigdata.evget.com/product/168.html