三硬币问题建模及Gibbs采样求解（Python实现）

三硬币问题建模及Gibbs采样求解（Python实现）

Gibbs采样原理介绍的文章有很多，但很少有Gibbs求解实际问题的例子。这篇博客通过三硬币问题，介绍如何用Gibbs采样求解实际问题。

三硬币问题

题目（摘自李航《统计学习方法》）：假设有3枚硬币，分别记做A，B，C。这些硬币正面出现的概率分别是π,p和q。进行如下掷硬币实验：先掷硬币A，根据其结果选出硬币B或C，正面选B，反面选硬币C；然后投掷选重中的硬币，出现正面记作1，反面记作0；独立地重复n次（n=10)，观测结果如下：

1111110000

假设只能观察投掷硬币的结果，不能观测投掷硬币的过程，估计这三个参数π,p和q。

二项分布与Beta分布

基础概念

介绍贝塔分布(Beta distribution)之前，需要先明确一下先验概率分布、后验概率分布、似然函数以及共轭分布的概念。

• 先验概率分布：在尚未获取某些信息或者依据前，根据过去历史资料或者人的主观经验对随机变量$X$概率分布的估计。
• 后验概率分布：通过调查或其它方式获取新的附加信息，利用贝叶斯公式对先验概率进行修正，而后得到的条件概率。
• 似然函数分布：是一个自变量是统计模型的参数的函数。
• 共轭分布：后验概率分布函数与先验概率分布函数具有相同形式。

二项分布

如果某个事件发生的概率为$p$，则独立重复$N$次实验时，该事件发生次数$x$的概率分布是二项分布，即$X\sim B(n,p)$其概率密度函数为：

$$P(X=k)=C_N^k{p}^k(1-p{)}^{n-k}$$

Beta分布

Beta分布是一组定义在区间$[0,1]$的连续概率分布，有两个参数$\alpha$和$\beta$，且$\alpha ,\beta >0$。Beta分布的概率密度函数：

$$Beta(p|\alpha ,\beta )=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}{p}^{\alpha -1}(1-p{)}^{\beta -1}$$

记$B(\alpha ,\beta )=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}$，由概率定义：${\int }_0^{1}Beta(p|\alpha ,\beta )=1$可以得到：

$$\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}=\frac{{\int }_0^{1}Beta(p|\alpha ,\beta )}{B(\alpha ,\beta )}=\frac{1}{B(\alpha ,\beta )}$$

Beta分布的期望为：

$$E(Beta(p|\alpha ,\beta ))=\frac{\alpha }{\alpha +\beta }$$

二项分布-Beta分布

根据贝叶斯公式有：

$$后验概率=似然函数\times 先验概率$$

对于观测结果为$X=\{x_1,x_2,\dots ,x_n\}$的二项分布，其似然函数为：

$$P(X|p)=p^k(1-p{)}^{n-k}$$

其中$k$为事件发生的次数。

如果参数$p$的先验概率分布为Beta分布，则有：

$$\begin{array}{rl}P(p|X)& =\frac{P(X|p)P(p)}{\int P(X|p)P(p)}\\ & =\frac{P(X|p)Beta(p|\alpha ,\beta )}{\int P(X|p)Beta(p|\alpha ,\beta )dp}\\ & =\frac{p^k(1-p{)}^{n-k}\frac{1}{B(\alpha ,\beta )}{p}^{\alpha -1}(1-p{)}^{\beta -1}}{\int p^k(1-p{)}^{n-k}\frac{1}{B(\alpha ,\beta )}{p}^{\alpha -1}(1-p{)}^{\beta -1}dp}\\ & =\frac{p^{\alpha +k-1}(1-p{)}^{\beta +n-k-1}}{\int p^{\alpha +k-1}(1-p{)}^{\beta +n-k-1}dp}\\ & =\frac{p^{\alpha +k-1}(1-p{)}^{\beta +n-k-1}}{B(\alpha +k,\beta +n-k)}\\ & =Beta(p|\alpha +k,\beta +n-k)\end{array}$$

$P(p|X)$与$P(X|p)$都是Beta分布，因此Beta分布是二项分布的共轭先验分布。

三硬币问题建模过程

记最终的观测结果为$x=\{x_1,x_2,\dots ,x_n\}$，每次观测结果使用的硬币为$z=\{z_1,z_2,\dots ,z_n\}$

对于硬币k出现正反面符合伯努利分布，记作：

$$P(x|p_k)=p_k^x(1-p_k{)}^{1-x}$$

其中随机变量$x$的取值为0、1。

使用概率图表示，三硬币问题的过程如下图所示：

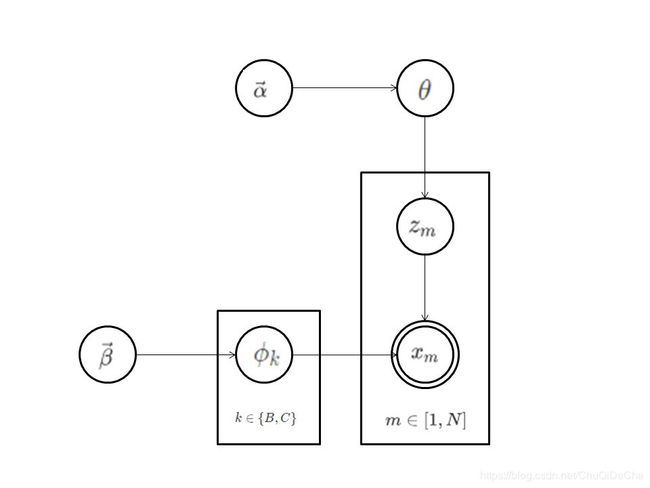
这个概率图可以分解成两个主要过程

1. $\alpha \to \theta \to z_m$：投掷硬币A，生成观测结果中第m次观测结果所使用的硬币编号。
2. $\beta \to {\varphi }_k\to x_m|z_m=k$：生成第m次观测结果时，首先选择编号为k的硬币，然后投掷这枚硬币，生成观测结果$x_m$

其中$\theta \to z$ 是二项分布，有：

$$P(z|\theta )={\theta }^k(1-\theta {)}^{n-k}$$

其中k为硬币A正面朝上的次数。

因$P(z|\theta )\sim B(n,p_A)$，可以取参数$\theta \sim Beta(\theta |\alpha )$，组成Binomial-Beta共轭分布，则后验分布：

$$P(\theta |z)\sim Beta(\theta |{\alpha }_1+k,{\alpha }_2+n-k)$$

$$\begin{array}{rl}P(z|\alpha )& =\int P(z|\theta )P(\theta |\alpha )d\theta \\ & =\int {\theta }^k(1-\theta {)}^{n-k}Beta(\theta |\alpha )d\theta \\ & =\int {\theta }^k(1-\theta {)}^{n-k}\frac{1}{B({\alpha }_1,{\alpha }_2)}{\theta }^{{\alpha }_1-1}(1-\theta {)}^{{\alpha }_2-1}d\theta \\ & =\frac{1}{B({\alpha }_1,{\alpha }_2)}\int {\theta }^k(1-\theta {)}^{n-k}{\theta }^{{\alpha }_1-1}(1-\theta {)}^{{\alpha }_2-1}d\theta \\ & =\frac{B({\alpha }_1+k,{\alpha }_2+n-k)}{B({\alpha }_1,{\alpha }_2)}\end{array}$$

有了参数的后验分布$P(\theta |z)$之后，参数$\theta$的合理取值可以是后验分布的极大值点或者参数在后验分布下的期望，此处取期望为参数的取值，则：

$$\theta =E(Beta(\theta |{\alpha }_1+k,{\alpha }_2+n-k))=\frac{{\alpha }_1+k}{({\alpha }_1+k)+({\alpha }_2+n-k)}$$
$n_1$和$n_2$分别表示使用硬币B和硬币C的次数。
如果已知每次观测结果来自哪枚硬币，任何两次观测结果都是可交换的，将来自同一枚硬币的观测结果放在一起

$$x^{\prime }=(x_B,x_C)$$

$$z^{\prime }=(z_B,z_C)$$

同上可知，对于来自硬币k的观测结果，同上$P(x_k|{\varphi }_k)\sim B(n_k,{\varphi }_k)$，参数${\varphi }_k\sim Beta({\varphi }_k|{\beta }_k)$，组成二项-Beta共轭分布，则后验分布：

$$P({\varphi }_k|x_k)\sim Beta({\varphi }_k|{\beta }_{k,1}+n_{k,1},{\varphi }_k|{\beta }_{k,2}+n_{k,2})$$

$$P(x_k|z_k,{\beta }_k)=\frac{B({\beta }_{k,1}+n_{k,1},{\beta }_{k,2}+n_{k,2})}{B({\beta }_{k,1},{\beta }_{k,2})}k\in \{B,C\}$$

$n_{k,1}$、$n_{k,2}$分别是k硬币出现正反面的次数

参数的值为：

$${\varphi }_k=\frac{{\beta }_{k,1}+n_{k,1}}{({\beta }_{k,1}+n_{k,1})+({\beta }_{k,2}+n_{k,2})}$$

因此有

$$\begin{array}{rl}P(x|z,\beta )& =P(x^{\prime }|z^{\prime },{\beta }^{\prime })\\ & =P(x_B,x_C|z_B,z_C,{\beta }_B,{\beta }_C)\\ & =P(x_B|z_B,{\beta }_B)P(x_C|z_C,{\beta }_C)\\ & =\frac{B({\beta }_{B,1}+k_B,{\beta }_{B,2}+n_B-k_B)}{B({\beta }_{B,1},{\beta }_{B,2})}\frac{B({\beta }_{C,1}+k_C,{\beta }_{C,2}+n_C-k_C)}{B({\beta }_{C,1},{\beta }_{C,2})}\end{array}$$

结合以上公式，可以得到联合分布：

$$p(x,z|\alpha ,\beta )=p(z|\alpha )p(x|z,\beta )=\frac{B({\alpha }_1+k,{\alpha }_2+n-k)}{B({\alpha }_1,{\alpha }_2)}\frac{B({\beta }_{B,1}+k_B,{\beta }_{B,2}+n_B-k_B)}{B({\beta }_{B,1},{\beta }_{B,2})}\frac{B({\beta }_{C,1}+k_C,{\beta }_{C,2}+n_C-k_C)}{B({\beta }_{C,1},{\beta }_{C,2})}$$

联合概率涉及到两个Binomial-Beta共轭结构。

Gibbs 采样求解

有了联合分布$p(x,z|\alpha ,\beta )$，就可以考虑使用Gibbs采样算法对这个分布进行采样。由于$x$是观测到的已知变量，只有$z$是隐含的变量。所以真正需要采样的是条件分$p(z|x)$。根据Gibbs采样算法的要求，需要求得任意一个坐标轴i对应的条件分布$p(z_i=k|z_{\neg i},x)$（$\neg i$表示去掉i）。假设已经观测到词$w_i=t$,根据贝叶斯公式可以得到：

$$\begin{array}{rl}p(z_i=k|z_{\neg i},x)& =p(z_i=k|x_i=t,z_{\neg i},x_{\neg i})\\ & =\frac{p(z_i=k,x_i=t|z_{\neg i},x_{\neg i})}{p(x_i=t|z_{\neg i},x_{\neg i})}\\ & \propto p(z_i=k,x_i=t|z_{\neg i},x_{\neg i})\end{array}$$

由于$z_i=k,x_i=t$仅会影响${\beta }_k\to {\varphi }_k\to x_i|z_i=k$一个共轭结构，且仅影响某些计数，因此$\theta$、${\varphi }_k$的后验分布仍然是Beta分布：

$$P(\theta |z_{\neg i},x_{\neg i})=Beta(\theta |\alpha +n_{\neg i})$$

$$P({\varphi }_k|z_{k,\neg i},x_{k,\neg i})\sim Beta({\varphi }_k|{\beta }_k+n_{k,\neg i})$$

去掉第i次观测值并不影响其他共轭结构，其他共轭结构与$z_i=k,x_i=t$是独立的，因此：

$$\begin{array}{rl}p(z_i=k|z_{\neg i},x)& \propto p(z_i=k,x_i=t|z_{\neg i},x_{\neg i})\\ & =p(z_i=k,x_i=t|z_{k,\neg i},x_{k,\neg i},z_{\neg k},x_{\neg k})\\ & =p(z_i=k,x_i=t|z_{k,\neg i},x_{k,\neg i})\end{array}$$

$x_{k,\neg i}$表示去除第i次观测所属k硬币的观测值。

所以，条件分布：

$$\begin{array}{rl}P(z_i=k|z_{\neg i},x)& \propto p(z_i=k,x_i=t|z_{k,\neg i},x_{k,\neg i})\\ & =\int P(z_i=k,x_i=t,\theta ,{\varphi }_k|z_{k,\neg i},x_{k,\neg i})d\theta d{\varphi }_k\\ & =\int P(z_i=k,\theta |z_{k,\neg i},x_{k,\neg i})P(x_i=t,{\varphi }_k|z_{k,\neg i},x_{k,\neg i})d\theta d{\varphi }_k\\ & =\int P(z_i=k,\theta |z_{k,\neg i},x_{k,\neg i})d\theta \int P(x_i=t,{\varphi }_k|z_{k,\neg i},x_{k,\neg i})d{\varphi }_k\\ & =\int P(z_i=k|\theta )P({\theta }_k|z_{k,\neg i},x_{k,\neg i})d\theta \int P(x_i=t|{\varphi }_k)P({\varphi }_k|z_{k,\neg i},x_{k,\neg i})d{\varphi }_k\\ & =\int \theta Beta(\theta |{\alpha }_k+n_{k,\neg i})d\theta \int {\varphi }_{k}Beta({\varphi }_k|{\beta }_k+n_{k,\neg i})d{\varphi }_k\\ & =E(\theta )E({\varphi }_k)\\ & =\hat{\theta }{\hat{\varphi }}_k\end{array}$$

因：

$$\hat{\theta }=\frac{n_{(k,\neg i),1}+{\alpha }_1}{(n_{(k,\neg i),1}+{\alpha }_1)+n_{(k,\neg i),2}+{\alpha }_2}$$

$${\hat{\varphi }}_k=\frac{{\beta }_{k,1}+n_{(k,\neg i),1}}{({\beta }_{k,1}+n_{(k,\neg i),1})+({\beta }_{k,2}+n_{(k,\neg i),2})}k=B,C$$

于是，得到最终模型的Gibbs采样公式：

$$P(z=k|z_{\neg i},x)\propto \frac{n_{(k,\neg i),1}+{\alpha }_1}{(n_{(k,\neg i),1}+{\alpha }_1)+n_{(k,\neg i),2}+{\alpha }_2}\cdot \frac{{\beta }_{k,1}+n_{(k,\neg i),1}}{({\beta }_{k,1}+n_{(k,\neg i),1})+({\beta }_{k,2}+n_{(k,\neg i),2})}k=B,C$$

python 实现

import random
K = 2 #最终观测结果来自的硬币个数
V = 2 #观测结果的取值个数（0,1）

X = [1,1,1,1,1,1,0,0,0,0] #观测结果
N = len(X) #观测次数
Z= [0] * N #每次观测结果对应的硬币编号

nz=[0,0] #cnz[i]硬币A掷出i面的次数（使用硬币i的次数）
nxz=[[0,0],[0,0]] #nzx[i][j] 观测结果为i来自j硬币的次数
nxsum = N #观测总次数
p=[0,0] #gibbs采样条件概率分布


alpha = 1 #硬币A Beta分布的 alpha、beta超参数,这里直接取<1,1>
beta=1  #硬币i Beta分布的 alpha、beta超参数,这里直接取<1,1>

max_iter = 100 #迭代次数

def init_params():
    # 对Z进行随机初始化
    for i in range(N) :
        prob = random.random()
        if prob > 0.5:
            Z[i] = 1
        else:
            Z[i] = 0
    # 统计
    for x,z in zip(X,Z):
        nxz[x][z] += 1
        nz[z] += 1
def sample():
    for cur_iter in range(max_iter):
        for i,x in enumerate(X,0):
            #去除观测结果i之后的计数
            z = Z[i]
            nz[z] -= 1
            nxz[x][z] -= 1
            global nxsum
            nxsum -= 1
            
            #计算条件分布
            for k in range(K):
                p[k] = (nxz[x][k] + beta)/(nz[k] +  V * beta)*(nz[k] + alpha)/(nxsum + K * alpha)
            
            #采样
            for k in range(1,K):
                p[k] = p[k-1] + p[k] 
            prob = random.random() * p[-1] #这里要进行归一化
            for k in range(K):
                if prob < p[k]:
                    z = k 
                    break
			
            nz[z] += 1
            nxz[x][z] += 1
            nxsum += 1
            Z[i] = z
init_params()
sample()

print((nz[1] + alpha)/(nxsum + K * alpha)) #硬币A正面朝上的概率
print((nxz[1][1] + beta)/(nz[1] +  V * beta)) #硬币B正面朝上的概率
print((nxz[0][1] + beta)/(nz[0] +  V * beta)) #硬币C正面朝上的概率

参考

1. 李航《统计学习方法》
2. GibbsLDA++ 源码
3. 靳志辉《LDA数学八卦》