计算机组成原理复习2(数据的表示和运算)
数制与编码
1.进位计数法
基数是每个数位所用到的不同数码的个数
2.不同进制数之间的相互转换
- 2进转换8进制:凑足3位,高位补0
- 2进制转换16进制:凑足4位,高位补0
- n任意转化为十进制:各个位上的数乘以n的(位数-1)次幂
- 除基取余法+乘积取整法
3.校验码
校验码是指能够发现或能够自动纠正错误的数据编码,也称为检错纠错编码;
原理:通过增加一些冗余码,来检验纠错编码
奇偶校验码:若干位有效信息,再加上一个二进制位组成校验码(0/1);判断整个校验码(有效信息位和校验位)中1的个数奇与偶
海明校验码:可以纠错,L最小码距越大检测错误的位数D越大,纠正错误的位数C也越大;L-1=D+C (且D>=C)
n+k<=2^k -1(n为有效信息的位数,k为校验码位数)
循环冗余校验码(CRC):基本思想是在K位信息码后再拼接R位的校验码,整个编码的长度为N位;
定点数的表示与运算
1.机器数的定点表示
定点小数:纯小数,约定小数点位置在符号位之后,有效数值部分最高值之前
定点整数:纯整数,约定小数点位置在有效数值部分最低位之后
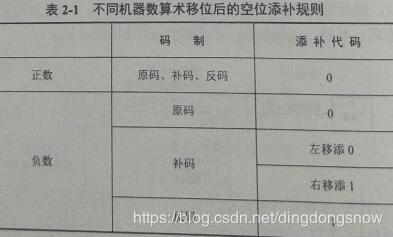
2.原码,补码,反码,移码(正数:反码=原码=补码)
原码:最高位为符号位 ;负小数1+|X|
原码加减法-先比较绝对值大小,绝对值大的减小的
补码:
纯小数x:x在0~-1期间 x=2-|x|
纯整数x:字长n 2^n - | x |
原码求补码(负数):符号不变,数值部分按位取反,末位加一
补码x算术移位:将符号位与数值位一起右移一位并保持原符号位的值不变
反码:原码按位取反(负数)
移码:
常用来表示浮点数的阶码,只能表示整数
移码就是在真值X上加一个常数(2^n偏移值)
3.定点数的移位运算
根据操作对象的不同,分为算术移位(有符号)和逻辑移位
算术移位:带符号,符号位不变
原码左移一位若不溢出,相当于乘以2 ;右移一位相当于除以2
逻辑移位:逻辑左移,高位移丢,地位添0,逻辑右移,低位移丢,高位添0
4.定点数的除法运算
原码除法运算:主要采用原码不恢复余数法(原码交替除法)
补码除法运算:特点是符号位与数值位一起参加运算,商符自然形成;第一步根据被除数和除数的符号决定是加法还是减法(同号相减,异号相加);上商原则根据余数和除数的符号位共同决定,同号上1 异号上0,最后一步商恒置1;
【X】补求【-X】补:【X】补连同符号位一起变反,末尾加一
浮点数的表示与运算
在位数有限的情况下,既扩大了数的表示范围,有保持了数的有效精度
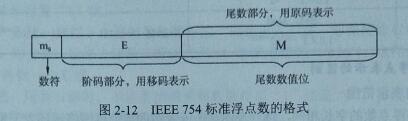
1.浮点数的表示格式
N=r^E*M(r是浮点数阶码的底,与尾数的基数相同,通常r=2,E和M都是带符号的定点数,E称为阶码,M称为尾数)
| 阶符J | 阶码的数值部分 | 数符 | 尾数的数值部分 |
阶码是整数,阶符和阶码的位数m合起来反映浮点数的表示范围及小数点的实际位置,尾数的位数n反映浮点数的精度
2.规格化浮点数
- 规格化操作是调整一个非规格化浮点数的尾数和阶码的大小
- 左规:算术左移,阶码加1
- 右规:尾数算术右移一位,阶码加1(一次就好)
- 原码规格化数的尾数最高一定是1,补码规格化数的尾数最高位一定与尾数符号位相反。基数不同,规格化形式不同
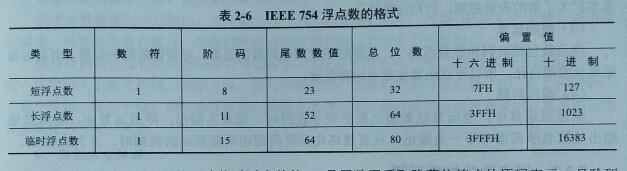
3.IEEE 754 标准
浮点数格式:
规格化的短浮点数真值:(-1)^s * 1.M* 2^(E-127) E取值1~254
规格化的长浮点数真值:(-1)^s * 1.M* 2^(E-1023) E取值1~2046
s=0表示正数,s=1时表示负数
4.定点,浮点表示的区别
(字长相同)
- 数值表示范围浮点范围大
- 数的精度浮点降低了
- 数的运算:浮点复杂,需要运算阶码和尾数
- 溢出:顶点中超出数的范围发生溢出,浮点中规格化后阶码超出范围发生溢出
5.浮点数的加减法(采用补码)
1.对阶: 使两个操作数的小数点位置对齐(阶码相等);求阶差,小阶向大阶看齐,小阶右移一位
2.尾数求和:将对阶后的尾数按定点数运算
3.规格化:
尾数大于0,补码规格化: 00.1xxx...x
尾数小于0,补码规格化: 11.0xxx...x
左规:当尾数出现00.0xxx或11.1xxx时需要左规,尾数左移,阶数-1,直到00.1xxx或11.0xxx
右规:当尾数求和溢出时(10.xxxx/01.xxxx)
4.含入;
0/1 舍入法:右移时移去的最高数值位为0,舍去,为1,尾数末位加1
恒置1法:恒加1
5.溢出判断:由阶码的符号决定
基数越大范围越大,精度低
原码表示时:正数规格化:0.1xxxx,负数规格化:1.1xxxx
G=AB
P=A异或B
C=G+PC'