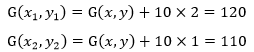A*搜索详解(1)——通往基地的最短路线

　　假设地图上有一片树林，坦克需要绕过树林，走到另一侧的军事基地，在无数条行进路线中，哪条才是最短的？

　　这是典型的最短寻径问题，可以使用A*算法求解。A*搜索算法俗称A星算法，是一个被广泛应用于路径优化领域的算法，它的行为的能力基于启发式代价函数，在游戏的寻路中非常有用。

将地图表格化

　　A*算法的第一个步是将地图表格化，具体来说是用一个大型的二维列表存储地图数据。这有点类似于像素画：

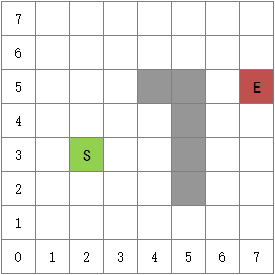
　　画中的小狗是由一个个像素方格组成的，方格越小，图案越平滑。在坦克寻径问题中，坦克的个头远小于地图，因此我们把坦克作为一个像素，这样一来，地图就可以切分为一个个方格，其中S代表坦克的起点，E代表基地：

　　我们把地图映射到二维列表上，每一方格都可以用唯一的二元组表示，元组的第一个维度是行号，第二个是列号，起点和终点的坐标分别是(3,2)和(5,7)。“找到坦克的最短路径”实际是在回答最短路径需要经过那些方格。

评估函数

　　A*算法的核心是一个评估函数：F(n)=H(n)+G(n)。

　　H(n)是距离评估函数，n代表地图上的某一个方格，H(n)的值是该方格到终点的距离。距离的计算方式有很多，选择不同的方式，计算的结果也不同：

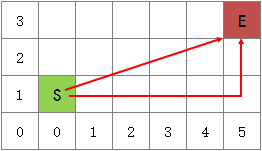
　　假设每个方格的边长都是1，如果用欧几里德距离S到计算S到E的距离，则：

　　如果用曼哈顿距离计算，则：

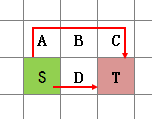
　　G(n)是从起点移动到n的代价函数，n离起点越远，付出的代价越高。起点达到n的路线有多条，每条路线的G值可能不同：

　　坦克从S到T的路线有两条，S→A→B→C→T和S→D→T，第二条路线更短，付出的代价也更低。假设从一个方格移动到相邻方格的代价是1，则G(D)=G(A)=1。B的前一步是A，因此G(B)=G(A)+1=2。同理，G(C)=G(B)+1=3。对于G(T)来说，它的值取决于T的上一步，如果路线是S→A→B→C→T，则G(T)=G(C)+1=4；如果路线是S→D→T，则G(T)=G(D)+1=2。值得注意的是，代价函数并不是唯一的，具体如何定义，完全取决于你自己。

　　某个位置的评估函数F仅仅是将该点的距离估值和代价值加起来。A*搜索的每一个寻径都会寻找评估值最小的点。

A*搜索的步骤

　　A*搜索涉及到两个重要的列表，openList（开放列表，存储候选节点）和closeList（关闭列表，存储已经走过的节点）。算法先把起放入openList中，然后重复下面步骤：

　　1. 遍历openList，找到F值最小的那个作为当前所在节点，用P表示；

　　2. 把P加入closeList中，作为已经走过的节点；

　　3. 探索P周围相邻且不在closeList中的每一个节点，记算它们的H值、G值和F值，并把P设置为这些方格的父节点，将这些节点作为待探索节点添加到Q中。当然，如何定义“相邻”也是你说的算。

　　4. 如果Q中的节点不在openList中，将其加入到openList。Q中的节点已经存在于openList中，比较这些节点的F值和它们在openList中的F值哪个更小（F越小说明这条路径越短），如果openList中的F值更小或二者相等，不做任何改变，否则用Q中的节点替换掉openList中的节点。

　　5. 如果终点在openList中，退出，最短路径就是从终点开始，沿着父节点移动直至起点；如果openList是空的，退出，此时意味着起点到终点没有任何路可走。

　　似乎不那么直观，我们仍然以坦克移动的例子审视这个过程。

通向基地的最短路线

　　在游戏开始之气，先要制定一些游戏规则。

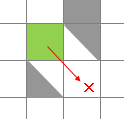
　　坦克可每一步都可以移动到与之相邻的八个方格中，我们指定每一个方格的边长是10，从一个方格移动到相邻方格的代价是这两个方格中心点的距离。如此一来，坦克上、下、左、右平移一格所花费的代价是10（这里之所以将边长定义为10而不是1，目的是为了避免向斜对角移动时产生小数），向斜对角移动的代价是：

　　下一步定义相邻的方格是否能够探索。如果坦克的相邻方格是障碍物，那么坦克无法移动到障碍物上，也无法贴着障碍物移动到斜对角的方格

　　不能移动到×所在的方格

探索最短路线

　　定义了游戏规则后就可以开始移动坦克。

　　我们定义地图是一个8×8的小地图，使用曼哈顿距离作为距离评估函数。以探索起点正上方的方格为例，它的位置是(4,2)，到起点的代价是G=10。

　　对于任意方格到终点的距离，我们不考虑障碍物，仅仅是简单的根据曼哈顿距离的公式计算。起点到终点的距离：

H(n) = H(4,2) = (|4 - 5| + |2 - 7|) * 10 = 60

　　这里乘以了系数10，这是由于我们在游戏规则中定义了方格的单位长度是10。

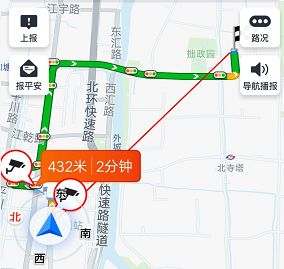
　　这有点类似于手机导航中的红色连线，这条连线仅仅连接了车标和终点，并不考虑中间是否有阻碍物：

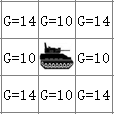
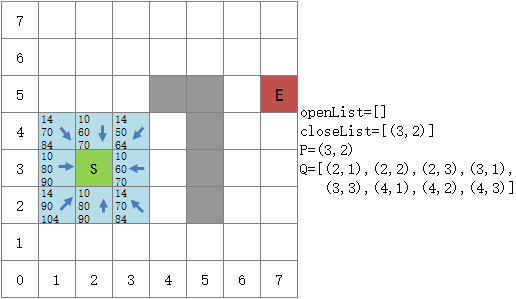
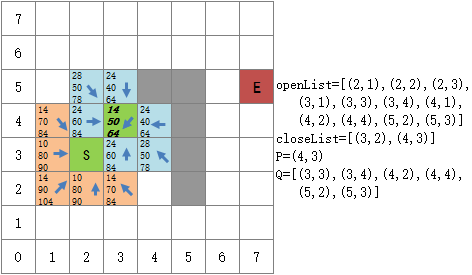
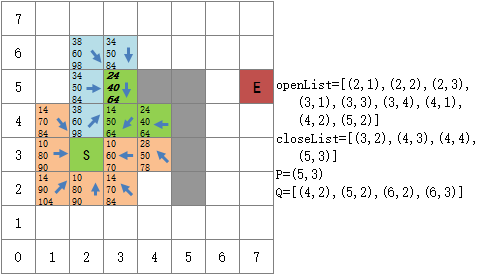
　　起点的G值是0，F=G+H=70。在待探索的八个方格中，我们设置从上到下的三个数值分别代表G、H、F，使用一个箭头指向是它的parent，箭头的指向不同，G值也可能不同：

　将S周围的方格设置为待探索方格

　　由于openList是空的，所以把 Q 中的8个待探索节点都放入openList中。此时的openList中，F(4,3) 最小，因此选择(4,3)作为下一个到达的位置，并把它从openList移至closeList

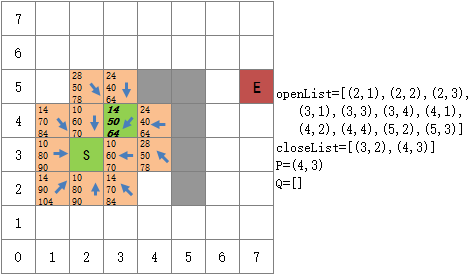
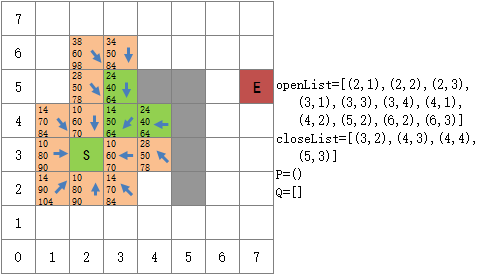
　　有八个方格与(4,3)相邻，其中(3,2)已经在closeList中，将它排除，(5,4)是障碍物，也排除，现在还剩六个，把它们都放入Q中：

将(4,3)相邻的可探索方格放到Q中

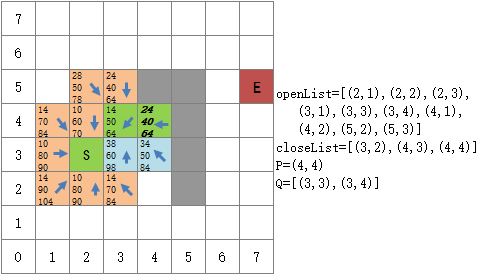
　　在Q的六个点中，(5,2),(5,3),(4,4),(3,4)是第一次探索，直接加入到openList中；(4,2),(3,3)已经存在于openList中，表示二者曾经被探索过。由于是从(4,3)探索(4,2)和(3,3)，因此二者的G值与从S点探索时的G值不同，即G_Q(4,2)≠G_openList(4,2)，G_Q(3,3)≠G_openList(3,3)，并且它们的父节点也不同。很明显，对于从S到(4,2)的两条路径来说，S→(4,3) →(4,2)要比S→ (4,2)更长，移动的代价更高，即G_Q(4,2)> G_openList(4,2)；同理，G_Q(3,3)>G_openList(3,3)。此时保留(4,2)和(3,3)在openList中的的数值和箭头指向：

保持openList中的(4,2)和(3,3)不变

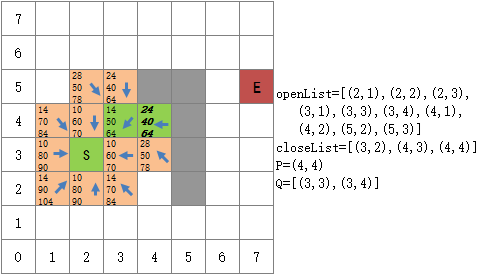
　　现在，openList中(5,3)和(4,4)的F值都是64，选择哪个都无所谓，这完全取决你自己制定的选取规则。这里我们用“胡乱选一个”的规则选择了(4,4)作为下一个目的地。与(4,4)相邻的八个方格中，四个是障碍物，一个在closeList中，还剩下(5,3),(3,3),(3,4)。根据游戏的规则，坦克无法“贴着障碍物移动到斜对角的方格”，因此(5,3)也要从待探索方格中去掉：

从(4,4)出发，可探索(3,3)和(3,4)

　　Q中的F(3,3)和F(3,4)都大于OpenList中的F(3,3)和F(3,4)，因此保留openList的元素不变：

保留openList的(3,3)和(3,4)

　　现在，openList的最小F值是F(5,3)=64，而(5,3)并不在Q中，说明对于路径S→(4,3)→(4,4)的探索失败了，但这并不妨碍我们从openList中挑选最小值F(5,3)=64。根据游戏规则，(5,3)周围有4个可供探索的方格：

从(5,3)出发，可探索(4,2), (5,2), (6,2), (6,3)

　　类似地，Q中的F(4,2)和F(5,2)都小于openList中的F(4,2)和F(5,2)，因此保持openList中的元素不变，将Q中的另外两个元素(6,2)和(6,3)移至openList中：

保持openList中的(4,2)和(5,2)不变，添加(6,2)和(6,2)

　　在openList中，(4,2)是最佳选择，而(4,2)并没有指向(5,3)，说明通过S→(4,3)→(5,3)并不能产生最佳路径。

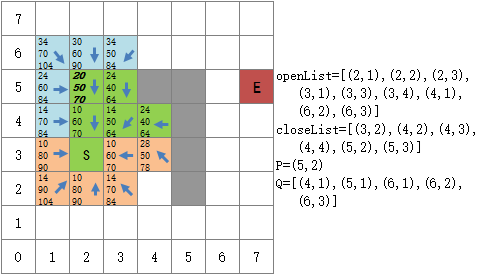
　　这个结论不妨碍继续执行A*搜索，再一次从openList中选择F值最小的元素(4,2)继续探索

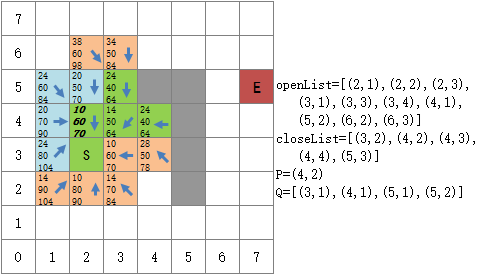
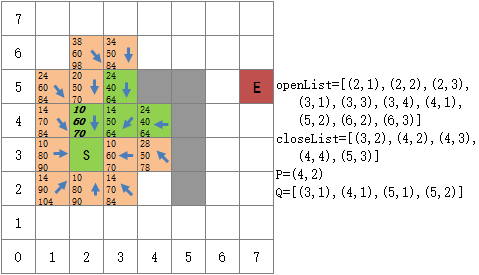
从(4,2)出发，可探索(3,1),(4,1),(5,1),(5,2)

　　在这一次探索中，Q中的最小F值F(5,2)=70已经小于openList中的F(5,2)=78，因此用Q中的(5,2)替换openList中的(5,2)，这将重新改变(5,2)的评估值和父节点：

用Q中的(5,2)替换openList中的(5,2)

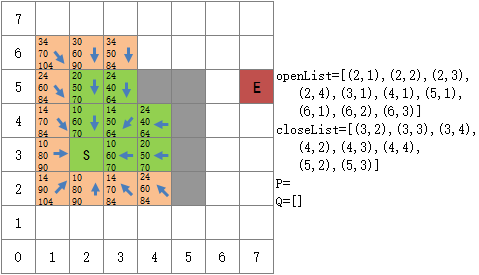
　　接下来从openLIst中选择(5,2)作为出发点，它周围可探索(4,1),(5,1),(6,1),(6,2),(6,3)这5个方格：

从(5,2)出发，可探索(4,1),(5,1),(6,1),(6,2),(6,3)

　　这次openLIst中的最小F值是F(3,3)=70。选择(3,3)后将会继续选择(3,4)，此时我们将又一次面对openLIst中有多个最小F值相等的情况：

openList中多个最小F值相等，F(4,1)=F(5,1) = F(6,3)=F(2,4)=F(2,3) =84

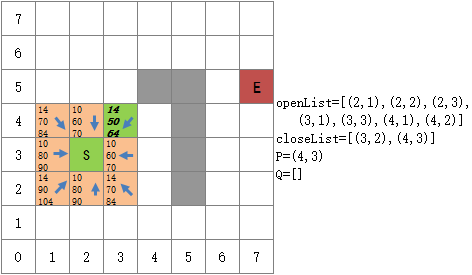
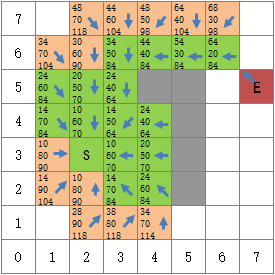
　　无论选择哪一个，最终都将得到同样的最短路径，假设(6,3)是这几个方格中最后选择的，则最终的结果：

　　从终点开始向前遍历，可以发现A*算法找到的最短路径是S→(4,3) →(5,3) →(6,3) →(6,4) →(6,5) →(6,6) →E。

　　可以看出，A*搜索和广度优先搜索十分类似，二者的候选集相同，它们的主要区别在于，广度优先搜索的选择是盲目的，而A*搜索是优先选择出代价最小的那个，利用启发的方式，使得每一步都更接近于最优解。

 

构建数据模型

　　地图上的每一个方格都是一个节点，我们将节点信息映射为Node类：

class Node:
    def __init__(self, x, y, parent, g=0, h=0):
        self.x = x  # 节点的行号
        self.y = y  # 节点的列号
        self.h = h
        self.g = g
        self.f = g + h
        self.parent = parent  # 父节点

    def get_G(self):
        '''
        当前节点到起点的代价
        :param parent:
        :return:
        '''
        if self.g != 0:
            return self.g
        elif self.parent is None:
            self.g = 0
        # 当前节点在parent的垂直或水平方向
        elif self.parent.x == self.x or self.parent.y == self.y:
            self.g = self.parent.get_G() + 10
        # 当前节点在parent的斜对角
        else:
            self.g = self.parent.get_G() + 14
        return self.g

    def get_H(self, end):
        '''
        节点到终点的距离估值
        :param end:  终点坐标(x,y)
        :return:
        '''
        if self.h == 0:
            self.h = self.manhattan(self.x, self.y, end[0], end[1]) * 10
        return self.h

    def get_F(self, end):
        '''
        节点的评估值
        :param: end 终点坐标
        :return:
        '''
        if self.f == 0:
            self.f = self.get_G() + self.get_H(end)
        return self.f

    def manhattan(self, from_x, from_y, to_x, to_y):
        ''' 曼哈顿距离 '''
        return abs(to_x - from_x) + abs(to_y - from_y)

　　每个节点都能够计算出自己的G值、H值和F值。在get_G()中，计算G值需要使用parent.get_G()，这是一种递归调用，为了避免递归的无用功，如果当前节点的G值已经计算过了，get_G()将直接返回结果。

　　接下来可以编写坦克寻径的代码，先来看一些基础结构：

class Tank_way:
    ''' 使用A*搜索找到坦克的最短移动路径 '''
    def __init__(self, start, end, map2d, obstruction=1):
        '''
        :param start: 起点坐标(x,y)
        :param end:   终点坐标(x,y)
        :param map:   地图
        :param obstruction: 障碍物标记
        '''
        self.start_x, self.start_y = start
        self.end = end
        self.map2d = map2d
        self.openlist = {}
        self.closelist = {}
        # 垂直和水平方向的差向量
        self.v_hv = [(-1, 0), (0, 1), (1, 0), (0, -1)]
        # 斜对角的差向量
        self.v_diagonal = [(-1, 1), (1, 1), (1, -1), (-1, -1)]
        self.obstruction = obstruction # 障碍物标记
        self.x_edge, self.y_edge = len(map2d), len(map2d[0]) # 地图边界
        self.answer = None

    def is_in_map(self, x, y):
        ''' (x, y)是否中地图内 '''
        return 0 <= x < self.x_edge and 0 <= y < self.y_edge

    def in_closelist(self, x, y):
        ''' (x, y) 方格是否在closeList中 '''
        return self.closelist.get((x, y)) is not None

    def upd_openlist(self, node):
        ''' 用node 替换 openlist中的对应数据 '''
        self.openlist[(node.x, node.y)] = node

    def add_in_openlist(self, node):
        ''' 将node添加到 openlist '''
        self.openlist[(node.x, node.y)] = node

    def add_in_closelist(self, node):
        ''' 将node添加到 closelist '''
        self.closelist[(node.x, node.y)] = node

    def pop_min_F(self):
        ''' 弹出openlist中F值最小的节点 '''
        key_min, node_min = None, None
        for key, node in self.openlist.items():
            if node_min is None:
                key_min, node_min = key, node
            elif node.get_F(self.end) < node_min.get_F(self.end):
                key_min, node_min = key, node
        # 将node_min从openlist中移除
        if key_min is not None:
            self.openlist.pop(key_min)
        return node_min

　　我们使用二维列列表存储地图上的每一个方格，用1表示障碍物，0表示可走的道路。openList和closeList使用字典代替列表，key是方格的坐标，value是表方格的节点，这将比列表更便于执行中A*搜索中的相关操作。

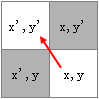
　　注意到这里并没有像5.5.1那样用一个列表存储八个方向的差向量，而是将斜对角的向量拆分出来，这样做的目的是便于应对游戏规则中“无法贴着障碍物移动到斜对角的方格”这一规则。假设某个方格的坐标是(x,y)，现在想要移动到左上方的(x’,y’)。能够移动的前提是(x,y)附近的两个方格都不是障碍物，可以用(x,y’)和(x’,y)来定位它们：

　　这种方法的好处是，只要知道(x,y)和(x’,y’)，就可以判断是否存在阻挡移动的障碍物，而无需关心(x’,y’)具体在什么方向：

　　根据这种思路编写用于寻找待探索节点的方法：

    def get_Q(self, P):
        ''' 找到P周围可以探索的节点 '''
        Q = {}
        # 将水平或垂直方向的相应方格加入到Q
        for dir in self.v_hv:
            x, y = P.x + dir[0], P.y + dir[1]
            # 如果(x,y)不是障碍物并且不在closelist中，将(x,y)加入到Q
            if self.is_in_map(x, y) \
                    and self.map2d[x][y] != self.obstruction \
                    and not self.in_closelist(x, y):
                Q[(x, y)] = Node(x, y, P)
        # 将斜对角的相应方格加入到Q
        for dir in self.v_diagonal:
            x, y = P.x + dir[0], P.y + dir[1]
            # 如果(x,y)不是障碍物，且(x,y)能够与P联通，且(x,y)不在closelist中，将(x,y)加入到Q
            if self.is_in_map(x, y) \
                    and self.map2d[x][y] != self.obstruction \
                    and self.map2d[x][P.y] != self.obstruction \
                    and self.map2d[P.x][y] != self.obstruction \
                    and not self.in_closelist(x, y):
                Q[(x, y)] = Node(x, y, P)
        return Q

实现A*搜索

　　A*搜索的完整代码：

class Node:
    def __init__(self, x, y, parent, g=0, h=0):
        self.x = x  # 节点的行号
        self.y = y  # 节点的列号
        self.h = h
        self.g = g
        self.f = g + h
        self.parent = parent  # 父节点

    def get_G(self):
        '''
        当前节点到起点的代价
        :param parent:
        :return:
        '''
        if self.g != 0:
            return self.g
        elif self.parent is None:
            self.g = 0
        # 当前节点在parent的垂直或水平方向
        elif self.parent.x == self.x or self.parent.y == self.y:
            self.g = self.parent.get_G() + 10
        # 当前节点在parent的斜对角
        else:
            self.g = self.parent.get_G() + 14
        return self.g

    def get_H(self, end):
        '''
        节点到终点的距离估值
        :param end:  终点坐标(x,y)
        :return:
        '''
        if self.h == 0:
            self.h = self.manhattan(self.x, self.y, end[0], end[1]) * 10
        return self.h

    def get_F(self, end):
        '''
        节点的评估值
        :param: end 终点坐标
        :return:
        '''
        if self.f == 0:
            self.f = self.get_G() + self.get_H(end)
        return self.f

    def manhattan(self, from_x, from_y, to_x, to_y):
        ''' 曼哈顿距离 '''
        return abs(to_x - from_x) + abs(to_y - from_y)

class Tank_way:
    ''' 使用A*搜索找到坦克的最短移动路径 '''
    def __init__(self, start, end, map2d, obstruction=1):
        '''
        :param start: 起点坐标(x,y)
        :param end:   终点坐标(x,y)
        :param map:   地图
        :param obstruction: 障碍物标记
        '''
        self.start_x, self.start_y = start
        self.end = end
        self.map2d = map2d
        self.openlist = {}
        self.closelist = {}
        # 垂直和水平方向的差向量
        self.v_hv = [(-1, 0), (0, 1), (1, 0), (0, -1)]
        # 斜对角的差向量
        self.v_diagonal = [(-1, 1), (1, 1), (1, -1), (-1, -1)]
        self.obstruction = obstruction # 障碍物标记
        self.x_edge, self.y_edge = len(map2d), len(map2d[0]) # 地图边界
        self.answer = None

    def is_in_map(self, x, y):
        ''' (x, y)是否中地图内 '''
        return 0 <= x < self.x_edge and 0 <= y < self.y_edge

    def in_closelist(self, x, y):
        ''' (x, y) 方格是否在closeList中 '''
        return self.closelist.get((x, y)) is not None

    def upd_openlist(self, node):
        ''' 用node 替换 openlist中的对应数据 '''
        self.openlist[(node.x, node.y)] = node

    def add_in_openlist(self, node):
        ''' 将node添加到 openlist '''
        self.openlist[(node.x, node.y)] = node

    def add_in_closelist(self, node):
        ''' 将node添加到 closelist '''
        self.closelist[(node.x, node.y)] = node

    def pop_min_F(self):
        ''' 弹出openlist中F值最小的节点 '''
        key_min, node_min = None, None
        for key, node in self.openlist.items():
            if node_min is None:
                key_min, node_min = key, node
            elif node.get_F(self.end) < node_min.get_F(self.end):
                key_min, node_min = key, node
        # 将node_min从openlist中移除
        if key_min is not None:
            self.openlist.pop(key_min)
        return node_min

    def get_Q(self, P):
        ''' 找到P周围可以探索的节点 '''
        Q = {}
        # 将水平或垂直方向的相应方格加入到Q
        for dir in self.v_hv:
            x, y = P.x + dir[0], P.y + dir[1]
            # 如果(x,y)不是障碍物并且不在closelist中，将(x,y)加入到Q
            if self.is_in_map(x, y) \
                    and self.map2d[x][y] != self.obstruction \
                    and not self.in_closelist(x, y):
                Q[(x, y)] = Node(x, y, P)
        # 将斜对角的相应方格加入到Q
        for dir in self.v_diagonal:
            x, y = P.x + dir[0], P.y + dir[1]
            # 如果(x,y)不是障碍物，且(x,y)能够与P联通，且(x,y)不在closelist中，将(x,y)加入到Q
            if self.is_in_map(x, y) \
                    and self.map2d[x][y] != self.obstruction \
                    and self.map2d[x][P.y] != self.obstruction \
                    and self.map2d[P.x][y] != self.obstruction \
                    and not self.in_closelist(x, y):
                Q[(x, y)] = Node(x, y, P)
        return Q

    def a_search(self):
        while True:
            #  找到openlist中F值最小的节点作为探索节点
            P = self.pop_min_F()
            # openlist为空，表示没有通向终点的路
            if P is None:
                break
            # P加入closelist
            self.add_in_closelist(P)
            # P周围待探索的节点
            Q = self.get_Q(P)
            # Q中没有任何节点，表示该路径一定不是最短路径，重新从openlist中选择
            if Q == {}:
                continue
            # 找到了终点， 退出循环
            if Q.get(self.end) is not None:
                self.answer = Node(self.end[0], self.end[1], P)
                break

            # Q中的节点与openlist中的比较
            for item in Q.items():
                (x, y), node_Q = item[0], item[1]
                node_openlist = self.openlist.get((x, y))
                # 如果node_Q不在openlist中，直接将其加入openlist
                if node_openlist is None:
                    self.add_in_openlist(node_Q)
                # node_Q的F值比node_openlist更小，则用node_Q替换node_openlist
                elif node_Q.get_F(self.end) < node_openlist.get_F(self.end):
                    self.upd_openlist(node_Q)

    def start(self):
        node_start = Node(self.start_x, self.start_y, None)
        self.openlist[(self.start_x, self.start_y)] = node_start
        self.a_search()

    def paint(self):
        ''' 打印最短路线 '''
        node = self.answer
        while node is not None:
            print((node.x, node.y), 'G={0}, H={1}, F={2}'.format(node.g, node.h, node.get_F(self.end)))
            node = node.parent

if __name__ == '__main__':
    map2d = [[0] * 8 for i in range(8)]
    map2d[5][4] = 1
    map2d[5][5] = 1
    map2d[4][5] = 1
    map2d[3][5] = 1
    map2d[2][5] = 1
    start, end = (3, 2), (5, 7)
    a_way = Tank_way(start, end, map2d)
    a_way.start()
    a_way.paint()

　　运行结果：

代价因子

　　坦克寻径的故事并没有结束，还可以额外考虑游戏中的两种典型的情况。一种是我们之前定义的“无法贴着障碍物移动到斜对角的方格”并不那么准确，如果障碍物只是占据了单元格的一部分位置，坦克也许可以挤过去：

　　另一个情况在游戏中更为常见，坦克其实是可以穿过树林的，只不过在树林中行进远远慢于在大路上行进。这类似于电视中的桥段：大路远但好走，小路近而难行，至于最终哪个更省力，全靠运气——也许小路由于刚下过一场雨导致更加难走，克服困难的成本远大于原计划节省的成本。为了应对这种情况，可以为每个方格添加一个代价因子，一个方格的代价因子越高，移动到这里的代价越大。例如某一点(x,y)的G值是G(x,y)=100，向垂直和水平方向的相邻方格移动一步的代价是10；左侧方格(x₁,y₁)是树林，移动因子是2；右侧方格(x₂,y₂)是平地，移动因子是1，此时：

　　

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”