梯度下降 Gradient Descent

θ ^* = argmin L(θ)

 

梯度方向：损失函数等高线的法线方向（切线方向，变化最快的方向）

θ ^t+1 = θ ^t - ηg(θ ^t)

 

关于梯度下降的Tips:

 

1. 调整学习率　adaptive learning rates

简单直觉的想法：训练刚开始的时候可以用比较大的学习率；经过一些epochs之后应该要减小学习率；比如说 1/t decay：η ^t  =  η / √(t+1)

更好的做法是每个参数都有不同的学习率  => 一个比较简单的方法是 adagrad

Adagrad：在 1/t decay 的基础上，不同参数的学习率除以过去（包括该当前时刻）该参数所有微分值的均方，这里 w 表示单个的参数

其中，t+1项消掉了

 

但是Adgrad在这里是否存在矛盾呢？

 

分子的微分项越大，更新的 step 就越大；但同时分母的历史梯度求和项就越大，反而导致 step 越小

直觉的解释：分母的项是为了造成一个反差的效果，如果 t 时刻的梯度和历史梯度的大小突然差别很大，就强调这种变化

 

更正式的解释：

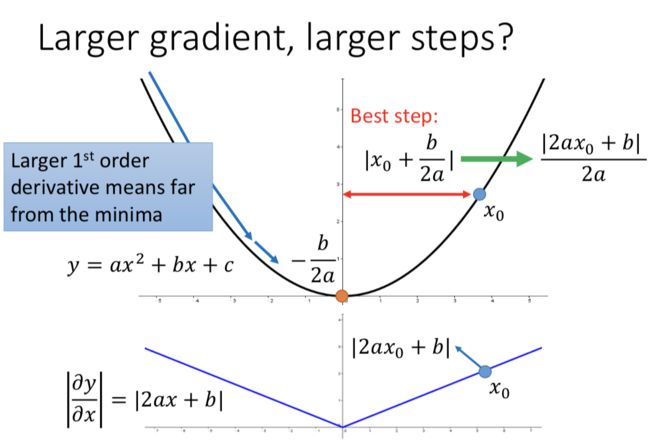
更大的梯度就意味着会走更大的step吗？或者说，一个最合理的step，跟梯度g的关系是什么样的？

只考虑一个参数：Larger gradient，Larger step，可以；更大的 1st order derivative 意味着离 minima 更远

 

但同时考虑多个参数时，这个结论有问题：（ 不能 cross parameters）

 

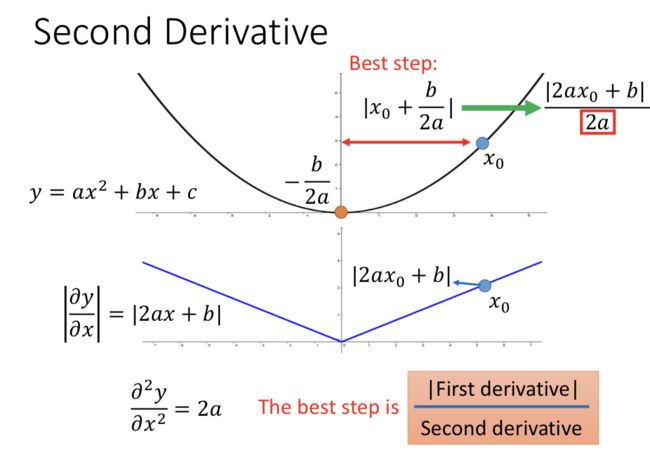
如果要跨参数？——  再考虑 second order derivative

 

最好的step：|first derivative| / second derivative，和一次微分成正比，和二次微分成反比，这样才能真正显示到 minima 的距离大小。

 

这和 Adagrad 的关系？

用足够多的一次微分的采样点，计算采样的平均值，去估计二次微分的大小趋势。（没有额外运算。当然也可以直接算二次微分，但是计算代价更大）

 

2. Stochastic Gradient Descent

原始的梯度下降是，全部训练样本都计算完了更新参数一次

stochastic gradient descent，每个样本都更新参数一次，会更快

而实际做的时候，会取一个batch更新一次

 

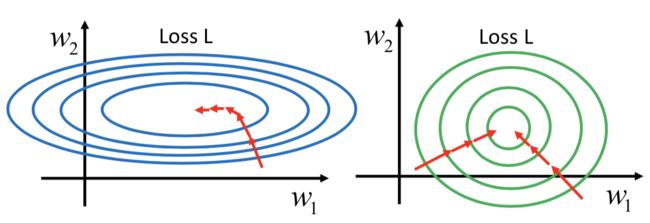
3. Feature Scaling

如果 x ₂ 的数量级大于 x ₁ ，改变 w ₂ 会对 loss 影响比较大，导致 w ₂ 方向更加 sharp，梯度下降优化过程中不同方向需要的学习率就非常不同。所以 feature scaling 会让优化过程更容易。

 

常见的做法是 standard scaling

For each dimension i :

　　mean: m _i

　　standard deviation: σ _i

　　x _i^r = (x _i - m _i) / σ _i

 

 

Gradient Descent 背后的理论 （为什么梯度下降能work）

如果用梯度下降解决一个优化问题，θ ^* = argmin L(θ)，那么每次更新参数都一定会使得损失函数变小吗？（一定能收敛吗？）

——不一定。原因？

 

假设损失函数有两个参数 {θ1, θ2}

给定一个点p，能够很容易的找出点p邻域内的最小值。 怎么做？ => 泰勒公式

只要h(x) 在x ₀的邻域无限可微，那么h(x)可以表示为

 

多变量的情况：

当 (x, y) 很接近 (x ₀, y ₀) 的时候，考虑用一阶微分项来近似。即，当处在  (x ₀, y ₀)  半径很小的邻域内时，利用泰勒公式来逼近损失函数 L：

其中L(a, b) 和两个微分项都是确定的常数，简化表示法，得到

 

那么就是要找 {θ1, θ2} 令 L 最小，s.t.

为了最小化 L，就选取和 (u, v) 内积最小的 (θ1 - a, θ2 - b)，显然就是 (u, v) 反方向，再正好 scale 到很小的直径d表示的圈边：

而 u 和 v 表示的正是梯度， 这个方法正是梯度下降：

所以，Gradient Descent 能 work 的前提条件是： learning rate 足够小（泰勒公式的逼近够精确）

 

梯度下降的局限：

1. 卡在局部极小值或者鞍点（微分值为0，但实际上这种情况很少，因为需要所有的方向都满足，参数越多这种情况发生概率越小）

2. 在plateau的阶段很慢（微分值很小，然后就停下了，但其实离 local minima 还很远）