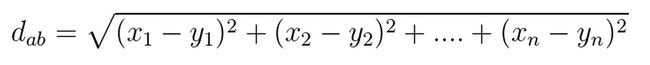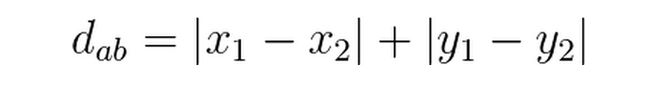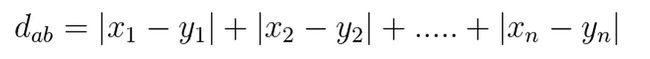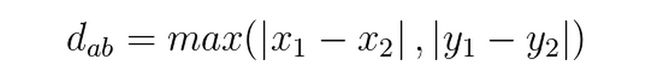相似度（距离计算）汇总

1 前言

在数据挖掘中，我们经常需要计算样本之间的相似度(Similarity ),我们通常的做法是计算样本之间的距离,本文对

距离计算方法做以下总结。

2 距离计算方法

A 欧式距离EuclideanDistance

欧式距离：两点之间的直线距离。

(1)二维平面上两点a(x₁,y₁)，b(x₂,y₂)之间的欧式距离公式：

(2) n维空间上两点a(x₁,x₂……..x_n)，b(y₁,y₂……..y_n)的欧式距离公式：

B  曼哈顿距离(ManhattanDistance)

       曼哈顿距离也叫”曼哈顿街区距离”。想象你在曼哈顿街道上，从一个十字路口开车到另一个十字路口，驾驶距离就

是这个“曼哈顿距离”。

(1)二维平面上两点a(x₁,y₁)，b(x₂,y₂)之间的曼哈顿距离公式：

(2) n维空间上两点a(x₁,x₂……..x_n)，b(y₁,y₂……..y_n)的曼哈顿距离公式：

C 夹角余弦

机器学习中可以把两点看成是空间中的两个向量，通过衡量两向量之间的相似性来衡量样本之间的相似性。

(1)二维平面上两向量a(x₁,y₁)，b(x₂,y₂)之间的夹角余弦公式：

也可直接通过向量运算：

(2) n维空间上两点a(x₁,x₂……..x_n)，b(y₁,y₂……..y_n)的夹角余弦公式：

D 切比雪夫距离（Chebyshevdistance）

切比雪夫距离:各对应坐标数值差的最大值。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？你会发现最少步

数总是max( | x2-x1 | , | y2-y1 | )步。

(1)二维平面上两点a(x₁,y₁)，b(x₂,y₂)之间的切比雪夫距离公式：

(2) n维空间上两点a(x₁,x₂……..x_n)，b(y₁,y₂……..y_n)的切比雪夫距离公式：

E 汉明距离

    两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。

  1011101与 1001001 之间的汉明距离是2  　

　

  2143896与 2233796 之间的汉明距离是3  　

　

  irie与 rise之间的汉明距离是 3

转自：http://blog.csdn.net/wangpei1949/article/details/52926651

当两条新闻向量夹角余弦等于1时，这两条新闻完全重复（用这个办法可以删除爬虫所收集网页中的重复网页）；当夹角的余弦值接近于1时，两条新闻相似（可以用作文本分类）；夹角的余弦越小，两条新闻越不相关。

 

2、余弦距离和欧氏距离的对比

从上图可以看出，余弦距离使用两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比欧氏距离，余弦距离更加注重两个向量在方向上的差异。

借助三维坐标系来看下欧氏距离和余弦距离的区别：

从上图可以看出，欧氏距离衡量的是空间各点的绝对距离，跟各个点所在的位置坐标直接相关；而余弦距离衡量的是空间向量的夹角，更加体现在方向上的差异，而不是位置。如果保持A点位置不变，B点朝原方向远离坐标轴原点，那么这个时候余弦距离  是保持不变的（因为夹角没有发生变化），而A、B两点的距离显然在发生改变，这就是欧氏距离和余弦距离之间的不同之处。

欧氏距离和余弦距离各自有不同的计算方式和衡量特征，因此它们适用于不同的数据分析模型：

欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异。

余弦距离更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦距离对绝对数值不敏感）。

 

3、杰卡德相似性度量

（1）杰卡德相似系数

两个集合A和B交集元素的个数在A、B并集中所占的比例，称为这两个集合的杰卡德系数，用符号 J(A,B) 表示。杰卡德相似系数是衡量两个集合相似度的一种指标（余弦距离也可以用来衡量两个集合的相似度）。

（2）杰卡德距离

与杰卡德相似系数相反的概念是杰卡德距离（Jaccard Distance），可以用如下公式来表示：

杰卡德距离用两个两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。

（3）杰卡德相似系数的应用

假设样本A和样本B是两个n维向量，而且所有维度的取值都是0或1。例如，A（0,1,1,0）和B（1,0,1,1）。我们将样本看成一个集合，1表示集合包含该元素，0表示集合不包含该元素。

p：样本A与B都是1的维度的个数

q：样本A是1而B是0的维度的个数

r：样本A是0而B是1的维度的个数

s：样本A与B都是0的维度的个数

那么样本A与B的杰卡德相似系数可以表示为：

此处分母之所以不加s的原因在于：

对于杰卡德相似系数或杰卡德距离来说，它处理的都是非对称二元变量。非对称的意思是指状态的两个输出不是同等重要的，例如，疾病检查的阳性和阴性结果。

按照惯例，我们将比较重要的输出结果，通常也是出现几率较小的结果编码为1（例如HIV阳性），而将另一种结果编码为0（例如HIV阴性）。给定两个非对称二元变量，两个都取1的情况（正匹配）认为比两个都取0的情况（负匹配）更有意义。负匹配的数量s认为是不重要的，因此在计算时忽略。

（4）杰卡德相似度算法分析

杰卡德相似度算法没有考虑向量中潜在数值的大小，而是简单的处理为0和1，不过，做了这样的处理之后，杰卡德方法的计算效率肯定是比较高的，毕竟只需要做集合操作。

 

4、调整余弦相似度算法（Adjusted Cosine Similarity）

余弦相似度更多的是从方向上区分差异，而对绝对的数值不敏感，因此没法衡量每个维度上数值的差异，会导致这样一种情况：

用户对内容评分，按5分制，X和Y两个用户对两个内容的评分分别为（1,2）和（4,5），使用余弦相似度得到的结果是0.98，两者极为相似。但从评分上看X似乎不喜欢2这个 内容，而Y则比较喜欢，余弦相似度对数值的不敏感导致了结果的误差，需要修正这种不合理性就出现了调整余弦相似度，即所有维度上的数值都减去一个均值，比如X和Y的评分均值都是3，那么调整后为（-2，-1）和（1,2），再用余弦相似度计算，得到-0.8，相似度为负值并且差异不小，但显然更加符合现实。

那么是否可以在（用户-商品-行为数值）矩阵的基础上使用调整余弦相似度计算呢？从算法原理分析，复杂度虽然增加了，但是应该比普通余弦夹角算法要强。

 转自：http://www.cnblogs.com/chaosimple/archive/2013/06/28/3160839.html

一、说明

相似性度量用以描述两个向量之间的相似性，是一个值域为一维的二元函数。一般情况，相似性度量本质上指距离度量，只不过数值指示刚好相反，如果是距离的话，数值越小，距离越近，而相似度越大；如果是相似度的话，数值越小，相似度越小，而距离越大。

相似性度量在机器学习中是一个非常基础的概念，尤其在聚类、推荐系统等算法中。

在工程应用中，也会使用一些不完全满足距离度量基本性质的“非距离度量”[1]。

二、距离度量的基本性质：

        非负性：dist(x,y) >= 0

        同一性：dist(x,x) = 0

        对称性：dist(x,y) = dist(y,x)

        三角不等式：dist(x,z)+dist(y,z) >= dist(x,y)

三、常用相似性度量

1、闵可夫斯基距离(Minkowski Distance)

2、曼哈顿距离(Manhattan Distance)

p=1时，闵可夫斯基距离就是曼哈顿距离

又称城市街区距离，在方正的北京大街打车，行车距离就是曼哈顿距离，如果在山城重庆就不是了。

3、欧氏距离(Euclidean Distance)

p=2时，闵可夫斯基距离就是欧氏距离。

在平面几何或者立体几何中的距离，通常就是欧氏距离，所以欧氏距离也最容易理解。

4、切比雪夫距离(Chebyshev Distance)

p等于无穷大时，闵可夫斯基距离就是切比雪夫距离。

若将国际象棋棋盘放在二维直角坐标系中，格子的边长定义为1，座标的x轴及y轴和棋盘方格平行，原点恰落在某一格的中心点，则王从一个位置走到其他位置需要的最少步数恰为二个位置的切比雪夫距离，因此切比雪夫距离也称为棋盘距离。[2]

5、"加权(weighted)"闵可夫斯基距离

当样本中不同属性的重要性不同时，可使用"加权距离"(weighted distance)[1]。

6、余弦相似度(Cosine Similarity)

余弦相似性取值[-1,1]，值越趋于1，表示两个向量的相似度越高。余弦相似度与向量的幅值无关，只与向量的方向相关，在文档相似度(TF-IDF)和图片相似性(histogram)计算上都有它的身影[3]。

7、皮尔逊相关系数(Pearson Correlation)

余弦相似度会受到向量的平移影响，怎样才能实现平移不变性？在余弦相似度的基础上，每个向量减去这个向量均值组成的向量，也就是皮尔逊相关系数，有时候也直接叫相关系数。

当两个向量均值都为0时，皮尔逊相对系数等于余弦相似性。

8、马氏距离(Mahalanobis Distance)

一个向量的不同维度如果是不同的量纲，更有甚者，维度之间是相关的，比如身高和体重组成的向量，在闵可夫斯基距离中等同对待，有时，这样是不恰当的。马氏距离利用 Cholesky transformation 消除了不同维度之间的相关性和尺度不同[3]。

其中，S为样本的协方差矩阵。当S是单位阵的时候，马氏距离就是欧式距离；当S是对角阵的时候，马氏距离是加权欧式距离。

很多时候，一个事物的有点也可能会构成它的缺点。这里马氏距离可以消除不同维度之间的不同尺度，就可能放大了变化细微维度的作用[4]。

我们可以按照连续性将属性分为“连续属性”和“离散属性”；也可以按照有序性将属性分为“有序属性”和“无序属性”[1]。上面的相似性度量都是关于“连续”并“有序”属性的，下面给出几个关于“离散属性”和“无序属性”的相似性度量。

9、汉明距离(Hamming Distance)

两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。

例如:字符串“11110011”与“10010010”之间的汉明距离为3。

汉明距离可以在通信中累计定长二进制字中发生翻转的错误数据位，所以它也被称为信号距离。汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。[5]

如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离等算法。[5]

10、杰卡德相似系数(Jaccard Similarity)

杰卡德相似系数是衡量两个集合的相似度一种指标

杰卡德相似系数是从相似性度量的角度来表述的，从距离度量的角度，则有杰卡德距离(Jaccard Distance)

杰卡德相似系数和杰卡德距离本质上是一样的，只是表述角度不同。

在聚类中，杰卡德相似系数可以作为聚类的性能度量[1]。在推荐系统中，杰卡德相似系数可以度量两个购买若干商品的用户之间的相似性[3]。

11、KL散度(Kullback-Leibler Divergence)

又叫相对熵，表示两个随机分布之间的相似性

可以证明，KL散度大于等于0，当p=q时等于0；KL散度不满足对称性。

12、Hellinger距离(Hellinger Distance)

在七月算法的课程里，还讲了一个与KL散度类似的距离，表示随机分布之间的相似性的Hellinger距离

当α=0时

这时，Hellinger距离就是两个随机分布取平方根之后的欧式距离，符合距离度量的四个性质，是严格的距离度量。

转自：http://www.jianshu.com/p/9b7166997a3e

总结：

• 如果数据存在“分数膨胀“问题，就使用皮尔逊相关系数
• 如果数据比较密集，变量之间基本都存在共有值，且这些距离数据都是非常重要的，那就使用欧几里得或者曼哈顿距离
• 如果数据是稀疏的，就使用余弦相似度