深度学习 查漏补缺篇章
本篇博客作为复习深度学习时，查漏补缺所用。
不是任何事情都要有一个直观的印象，像深度学习这种，很多东西你转化为对于数学的理解这一步就可以了。
——写给钻牛角尖的完美主义
感受野 深度理解
反卷积（deconvolution）的理解 +上采样(UNSampling)与上池化(UnPooling)
空洞卷积 （Dilated/Atrous Convolution ）的理解
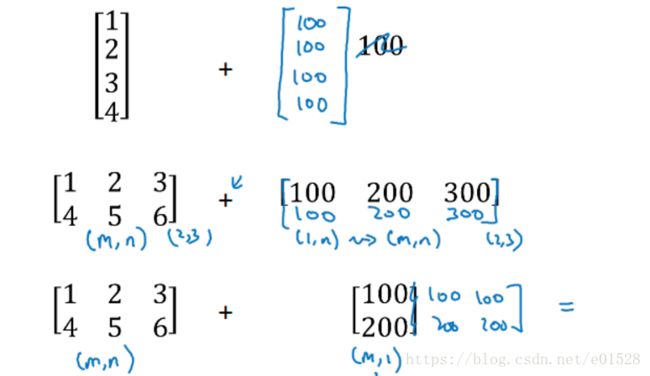
习惯性矩阵思维
目录
Part1. ng课程复习与思考
1. 在神经网络当中，x是 n行m列 ，m个样本，n表示特征向量 /* 列叠加 */
2. 为什么凸函数有利于梯度下降（优化）？
3. 为什么 归一化后加快了梯度下降求最优解的速度？
4. 为什么 归一化有可能提高精度？
5. 梯度下降大局观
6. logistic代价函数的解释
7. python中的广播 numpy和广播使我们可以用一行代码完成很多运算
8. assert(a.shape==(n,1))避免shape为(n,)的向量，reshape的使用
9. 激活函数小对比
Part1. ng课程复习与思考
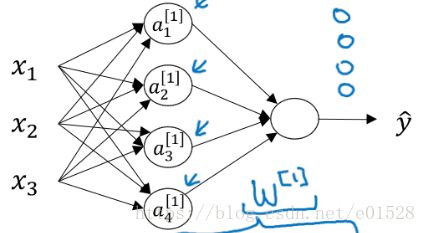
0. cnn 大局观
y^=wx+b，x是输入，w是特征权值向量。
w：往往我们说的3*3*256的卷积就是w了，
y^：通过卷积生成的（1,36，H，W）的就是y^，
y* ：gt对应的
L(y^,y*): y^和y*，做损失函数，通过优化器，迭代更新3*3*256的w卷积，学习到复杂的特征（就是w），来使得loss减少，预测的接近于真实的。
比如faster rcnn 中smooth l1 loss 使得rpn_box_pred(预测的偏移)接近于rpn_box_target(真实的偏移),降低loss的方法，就是不断学习调整各个w，以学习复杂特征。（在这个过程中利用gt在anchor_target_layer中，先删除边界框外的anchor，然后获得边界框内的rpn_box_inside，然后重新弄一个新的整个anchor的，统一赋值0，然后讲框内的rpn_box_inside 再利用之前的赋值，来确定哪一个是整个anchor中，正样本对应的anchor，只对他进行smooth l1 loss，也就是回归正anchor），
在这个过程中rpn_box_pred是直接在共享特征层进行3*3*256的卷积后，进行1*1*36的全卷积w（这个就是要学的w）生成y^（1,36，H，W），来存储预测的anchor。
而rpn_box_target则是通过寻找原始anchor最近的gt的方法，找到每个anchor对应的gt的偏移，用数学表达为：y*（1,36，H，W）的向量。其中（1,36，H，W）可以理解为(1,4,9*H,W)也就是每个anchor的4个偏移。
1. 在神经网络当中，x是 n行m列 ，m个样本，n表示特征向量 /* 列叠加 */
y=wt*x+b中的x是n行m列，脑子中不是想着下面的图1这种，而是矩阵np相乘
比如，本来x的shape是3*1，w是4*3，得到的z就是4*1，其中4代表4个隐藏层的单元数，1代表1个样本。
现在X是多个样本，是3*m，w还是4*3，得到的Z就是4*m，4代表隐藏层的单元数，m代表的是样本数。
向量化运算，尽量避免用for语句，比如m个样本，不用for i in range(m) n个特征。
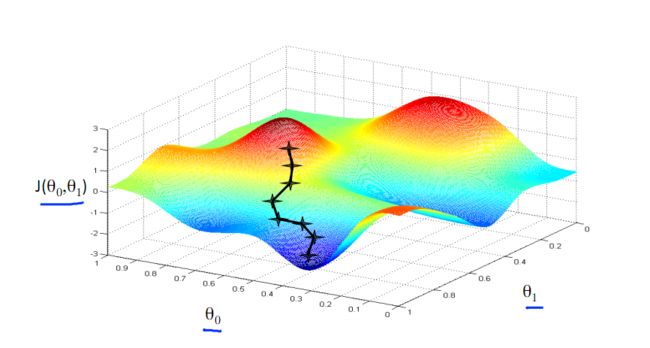
2. 为什么凸函数有利于梯度下降（优化）？
凸函数的性质：1.二阶可导 2.二阶导数>0 3.局部最优就是全局最优
梯度下降得到的结果可能是局部最优值。如果F(x)是凸函数，则可以保证梯度下降得到的是全局最优值。
下图为梯度下降的目的，找到J（θ）的最小值。
其实，J(θ)的真正图形是类似下面这样，其是一个凸函数，只有一个全局最优解，所以不必担心像上图一样找到局部最优解
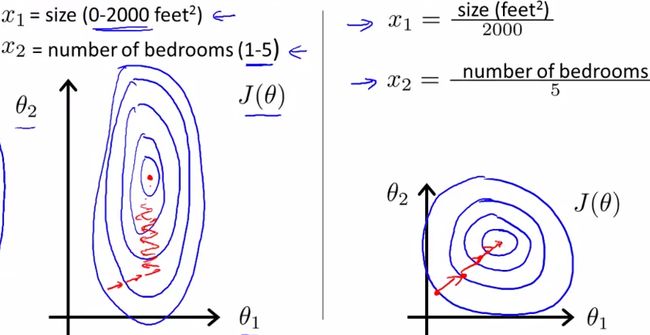
3. 为什么 归一化后加快了梯度下降求最优解的速度？
如下图所示，蓝色的圈圈图代表的是两个特征的等高线。其中左图两个特征X1和X2的区间相差非常大，X1区间是[0,2000]，X2区间是[1,5]，其所形成的等高线非常尖。当使用梯度下降法寻求最优解时，很有可能走“之字型”路线（垂直等高线走），从而导致需要迭代很多次才能收敛；
4. 为什么 归一化有可能提高精度？
一些分类器需要计算样本之间的距离（如欧氏距离），例如KNN。如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况相悖（比如这时实际情况是值域范围小的特征更重要）。
5. 梯度下降大局观
代价函数求导，更新 w=w−α∗J′(w)，通过更改w b使得到达最近似值。
6. logistic代价函数的解释
https://www.cnblogs.com/liaohuiqiang/p/7659719.html 7.1部分 【最大似然的思想使已有的数据发生的概率最大化，相乘最大】
7. python中的广播 numpy和广播使我们可以用一行代码完成很多运算
加减乘除都是
8. assert(a.shape==(n,1))避免shape为(n,)的向量，reshape的使用
比如a 的 shape是(5, ) ，当你计算np.dot(a,a.T)的时候得到的是一个实数，a和a的转置，它们的shape都是(5, )。
如果a 的 shape是(5, 1)，你计算np.dot(a,a.T)的时候得到的就是一个5*5的矩阵。a的shape是( 5, 1)，而a.T的shape是( 1, 5 )。
a.shape = (5, )这是一个秩为1的数组，不是行向量也不是列向量。很多学生出现难以调试的bug都来自秩为1数组。如果你得到了(5,) 你可以把它reshape成(5, 1)或(1, 5)，reshape是很快的O(1)复杂度
9. 激活函数小对比
通常来说，很少会把各种激活函数串起来在一个网络中使用的。
| sigmoid | tanh | relu | leakly relu | |
| 优点 | 1. 输出层还是使用sigmoid，因 2. 为它输出[0,1]更符合概率分布 |
关于原点 中心对称 |
1. ReLU 对于 SGD 的收敛有加速作用，有人认为是由于它的线性、非饱和所致。 2. ReLU 只需要一个阈值就可以得到激活值，不用去算一大堆复杂的（指数）运算 |
为解决“ ReLU 死亡”问题的尝试。 |
| 缺点 | 1. 不关于原点中心对称 2. 梯度消失 |
梯度消失 | 1.relu的缺点是当z小于等于0时导数为0 2. 它在训练时比较脆弱并且可能“死掉”。 合理设置学习率，会降低这种情况的发生概率。实在不行尝试 Leaky ReLU、PReLU 或者 Maxout.
|
1. 论文指出这个激活函数表现不错，但是其效果并不是很稳定。 2. Delving Deep into Rectifiers 中介绍了一种新方法PReLU，然而该激活函数在在不同任务中表现的效果也没有特别清晰。 |
10. dropout
dropout是为了防止过拟合的手段，当算法过拟合的时候才使用，所以一般是用在计算视觉方面（往往没有足够的数据，容易过拟合）
11. 归一化的平均值和方差
如果你在训练集归一化，那么在测试集要用相同的平均值和方差（训练集计算得到的）来归一化，因为我们希望在训练集和测试集上做相同的数据转换。
12. 梯度消失，梯度爆炸，权重初始化
ng的例子中，训练神经网络的时候如果网络很深的话，假设权重都是1.5，传递到最后一层的y的值将会呈指数增长（因为每经过一层就会乘一个权重1.5），假设权重都是0.5，传递到最后一层的y将会变得很小很小。
这是造成梯度消失或梯度爆炸的原因，它给训练造成了很大困难。针对梯度消失或梯度爆炸，有一个不完整的解决方案，虽然不能彻底解决问题，却很有用。
考虑z=w1∗x1+w2∗x2+...+wn∗xnz=w1∗x1+w2∗x2+...+wn∗xn，为了防止z太大或太小，可以看到n越大的话，你就希望w越小，以此来平衡z，那么很合理的设定就是把w设定为1/n。
所以在某一层，初始化权重的方法就是设定值为
，如下图所示，其中
表示l层的输入特征数。如果你使用的是relu激活，那么用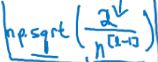
效果会更好。
此外，还有一些其它的变种，见下右图所示。权重初始化可以看做一个超参数，但是相比于其它超参数，它的优先级比较小，一般优先考虑调整其它超参数来调优。
13. 为什么权重初始化不能全为0或者相同的值？
初始化如果是相同的值，那么所有神经元的输出都将是相同的，这样在back propagation的时候同一层内所有神经元的行为也是相同的 ，也就是gradient相同，weight update也相同。也就是说所有的神经元进行的是一样的操作，这就起不到任何作用了，我们一般会随机初始化，但其实这样有时会导致梯度消失，权重很难更新，所以也引入了Xavier initialization，保证输入和输出的方差一样，现在蛮多人喜欢在每一层后面加上BN层，来达到好的效果。
优秀的初始化应该使得各层的激活值和状态梯度的方差在传播过程中的方差保持一致。
https://blog.csdn.net/shuzfan/article/details/51338178
http://www.cnblogs.com/hejunlin1992/p/8723816.html
14. 梯度的数值逼近，梯度检验