大象起舞:用PostgreSQL解海盗分金问题

张泽鹏(redraiment):51信用卡信贷业务高级架构师。
资深挖坑不填党:在51先后挖过风控、信审、数据支持等多个互金信贷相关的坑
冷技术控:51内 PostgreSQL、FreeBSD、Emacs、Lisp 等技术的宣传者
懒癌患者:拒绝重复,追求“元自动化”,将一切可自动化的工作自动化
背景介绍
今天午休期间刷微信,看到云和恩墨的盖总转了一条朋友圈,说杨长老在Oracle中用SQL解海盗分金问题(原文《无往不利:用SQL解海盗分金的利益最大化问题》,看完之后手痒,决定试试在 PostgreSQL 中解决该问题。
问题简述
有5个海盗分100个金币,通过抓阄决定了先后顺序,依次提出分赃方案,需得半数以上(含自己)同意才能通过,否则提方案的海盗就会被处死。现要求为第一个海盗提供最佳方案。
需求分析
原文中有提到用逆推的思路解决问题,但对问题的分析比较简短,所以我补充一下我的思考过程。
首先,从问题中可提炼出以下几点有用的信息:
海盗数量:5
金币数量:100
抓阄结果:顺序已决定,可给海盗编号为1-5
通过条件:赞成人数比例 > 50%
最佳方案:问题中海盗们需争取"保命"和"金币",并且前者比后者更重要,因此会产生以下三种结果,其中收益逐个递减
-
保命,且尽可能多地获得金币
保命,但没金币
没命
原问题假定所有的海盗都足够理智、足够聪明,言下之意是海盗们会权衡:当且仅当,同意当前方案带来的收益,高于拒绝当前方案带来的收益,才会同意。因此,为了让当前的方案通过,需要去贿赂至少50%的海盗,让他们的收益高于后续方案的收益。
这个过程和竞选总统很像。比如,特朗普承诺如果他能当总统,每位共和党成员都能得到一枚金币;而希拉里当总统,将只给每位民主党成员发一枚金币。利益虽然小,但两个党派成员都清楚,若非本党派人士担任总统,会连这一点小利益都没有,因此都会支持自己党派的成员,以获得这看似不大的最高收益。
任务拆解
综上所述,为了贿赂成功,得先了解竞争对手的行贿策略,在其基础上提供更高的收益(没命的海盗为其保命、保住命的海盗增加他金币的数量);为使行贿的成本最低,可优先贿赂在竞争对手方案中收益最低的群体。
这意味着,5个海盗的最佳策略依赖4个海盗的策略,4个海盗的策略依赖3个海盗的策略,依次类推。这个过程,就是原文中提的逆推过程:
1个海盗时,他直接拥有100个金币,即分配方案是:[100]
2个海盗时,无论提出何种方案,都不会超过前一个方案的收益100,所以第二个提方案的海盗不会同意任何方案,即第一个海盗在该场景必死,分配方案是:[null, 100]
3个海盗时,上一个方案中有一个海盗"没命",可以用"保命"去贿赂他,不用花金币,即最佳分配方案是:[100, 0, 0]
4个海盗时,同理,无论提何种方案,都无法超越100这个最高收益,所以有一个海盗一定会反对,剩下两个海盗在之前的方案中没有任何收益,只要给他们各1个金币即可:[98, 0, 1, 1]
5个海盗时,前面4个海盗都可以被贿赂,但根据最小成本原则,优先贿赂上一轮收益为0的海盗,再从收益是1的两位海盗中随机挑选一位,给他2个金币,因此有两套方案:[97, 0, 1, 2, 0] 或 [97, 0, 1, 0, 2]
程序设计
前文手工推导整个过程,现在就开始尝试用 SQL 来模拟这个过程。倒不是说 SQL 是解决该问题的最佳选择,而是想通过这个问题来学习和巩固 SQL 的知识。
数据结构
该问题中,每个海盗需要保存他的编号以及他的收益。标准 SQL 语言中,除了提供数值、字符串等基础数据类型,还支持数组这种复合数据类型,语法是`array[
一项保存海盗的编号,第二项保存海盗的收益,如果海盗"没命"则金额`null`。
例如,`array[2, null]`表示编号为2的海盗"没命"、`array[4, 98]`表示编号为4的海盗最高收益是98个金币。
分配策略--多个海盗的信息--也可采用数组保存,即二维的整型数组。例如上述2个海盗是的分配策略是:`array[[1, null], [2, 100]]`,即第一个海盗没命,第二个海盗有100个金币。
贿赂算法
根据前文的分析,实时贿赂的步骤如下:
1.分配策略根据每个海盗的收益排升序:
a)null(没命)最靠前
b)金额小的靠前
2.增加前一半的海盗的收益
一半的数量:排除自己,剩余海盗的总数`n`
`n`为偶数:一半的数量为`n / 2`
`n`为奇数:一半的数量为`(n + 1) / 2`
行贿策略
金额为 null 时,改成0
金额非 null 时,加1
3.调整后一半的海盗收益为0
成本升序
PostgreSQL原生未提供通用数组的排序功能(intarray插件中的sort函数只能用于非null的一位整型数组),要对二维整型数组结构的分配策略排序,需要先将数组展开成行记录(row),再用`order by`排序。
虽然PostgreSQL提供了`unnest`函数用于将数组展开成行,但它真正的功能是`flatten`,会拍平深层的结构。
例如:`select unnest(array[[1,2],[3,4]])` 会返回4行记录,而不是期望的2行记录。
因此,需要自己实现数组的一维展开功能。需要用到 `array_lower(anyarray, int)` 和 `array_upper(anyarray, int)` 两个函数分别获得数组下标的上边界和下边界,然后用 `generate_series` 生成下标序列。
注意:SQL 中的数组下标是从 `1` 开始。假设策略数组的名称是 `strategy`,则展开+排序的代码如下:
select
strategy[i][1] as id,
strategy[i][2] as amount
from
generate_series(array_lower(strategy, 1),
array_upper(strategy, 1)) as t(i)
order by
amount nulls first
其中 `nulls first` 是显示地指定 `null` 排在最前。PostgreSQL 中,`null` 默认比非 `null` 值大,因此升序时排在最后,降序时排在最前。可用 `nulls first` 或 `nulls last` 打破该默认行为。
标记同伙
为了判断哪些海盗属于同伙(前一半),需要给上述排好序的列表标注新的下标, PostgreSQL 中提供了 `row_number()` 窗口函数,可以获得当前行的行号;接着用函数 `array_length(anyarray, int)` 可获得数组的长度,最后一个需要贿赂的海盗的下标是 `(array_length(strategy, 1) + 1) / 2`。假设上述排好序的数据存入临时表 `strategies`,则计算每一个海盗的贿赂成本代码如下:
select
id,
amount,
case
-- 判断是否是同伙
when row_number() over () <= (array_length(strategy, 1) + 1) / 2
then coalesce(amount + 1, 0) -- 活着的海盗金币上涨,死了的海盗复活
else 0 -- 后一半的海盗没有任何金币
end as cost
from
strategies
分配方案
如果行贿的成本(`sum(cost)`)高于总金币数量(`100`),意味着无法得到超过半数的赞成,保持上一次的方案,即保留 `amount` 作为每个海盗的最大收益;否则,减去成本剩下的就是新增海盗的最高收益(`100 - sum(cost)`),其他海盗改用`cost`作为新一轮的最大收益。
在"数据结构"一节中已经提过,策略的数据结构是二维整数数组,前文为了排序,已将数组转成行记录,先需要使用 PostgreSQL 的窗口函数 `array_agg` 再将行记录转成数组,同时使用 `array_cat` 追加一个海盗信息。
假设上述标记好同伙的数据存入临时表 `strategies`,则计算分配方案的代码如下:
select
case
when sum(cost) <= 100 then -- 判断是否能存活
array_cat(array_agg(array[id, cost]),
array[[array_length(strategy, 1) + 1,
100 - sum(cost)]]::int[])
else
array_cat(array_agg(array[id, amount]),
array[[array_length(strategy, 1) + 1,
null]]::int[])
end
from
strategies
迭代
至此,已完成分配方案单次调整的功能:给定任意分配方案,能算出再增加一个海盗时的最优分配策略。为了得到5个海盗的最优解,只需把这个功能迭代5次即可;但迭代过程中每一次的输出都要作为下一次的输入。SQL正好提供了 `with recursive`,同时满足迭代和管道两个功能!
`with` 子句用于定义只在一个查询中存在的临时表,带上 `recursive` 关键字后,可执行递归查询,例如递归查询所有子类型。我一直觉得这个名字太容易误导,它的整个执行过程其实类似广度优先搜索(BFS),例如:
with recursive foo(n) as (
values (1), (3), (5) -- 队列初始状态
union all
select n + 3 from foo where n < 5
)
select * from foo;
这段递归查询代码功能等价于以下迭代的 Python 代码:
(queue, foo) = ([1, 3, 5], []) # 对应 values (1), (3), (5)
while queue:
n = queue.pop(0)
foo.append(n)
if n < 5: # 对应 where n < 5
queue.append(n + 3) # 对应 select n + 3
print foo # 对应 select * from foo
上述两端代码的执行结果都是:1、3、5、4、6、7,共6项数据。其中前三项`1`、`3`、`5`是队列初始化的数据,而`4`由`1`生成、`6`由`3`生成、`7`由`4`生成。
回到海盗分金的问题,假设把上一节的分配策略功能定义成一个函数`bribe`,则迭代的代码如下:
with recursive spoils(strategy) as (
values (array[[1, 100]]) -- 初始状态,一个海盗拿全部
union all
select
bribe(strategy) -- 生成下一个分配策略
from
spoils
where
array_length(strategy, 1) < 5
)
即在策略长度小于5时,反复生成新的策略。
完整代码
至此,需求中的所有功能点都有对应的 SQL 方案可解决:迭代5次后,选出数组长度(海盗人数)为5的方案即可。以下是完整的 SQL 代码,在 PostgreSQL 可直接执行:
with recursive spoils(strategy) as (
values (array[[1, 100]]) -- 初始状态,一个海盗拿全部
union all
select (
with strategies as ( -- 用嵌套的 with 子句计算到下一个状态的成本
select
*,
case
when row_number() over () <= (array_length(strategy, 1) + 1) / 2
then coalesce(amount + 1, 0)
else 0
end as cost
from (
select
strategy[i][1] as id,
strategy[i][2] as amount
from
generate_series(array_lower(strategy, 1),
array_upper(strategy, 1)) as t(i)
order by
amount nulls first
) as t
)
select
case
when sum(cost) <= 100 then -- 判断是否能存活
array_cat(array_agg(array[id, cost]),
array[[array_length(strategy, 1) + 1,
100 - sum(cost)]]::int[])
else
array_cat(array_agg(array[id, amount]),
array[[array_length(strategy, 1) + 1,
null]]::int[])
end
from
strategies
)
from
spoils
where
array_length(strategy, 1) < 5
)
select
5 + 1 - strategy[i][1] as id,
strategy[i][2] as amount
from (
select
strategy,
generate_series(array_lower(strategy, 1),
array_upper(strategy, 1)) as i
from
spoils
where
array_length(strategy, 1) = 5
) as t
order by
id;
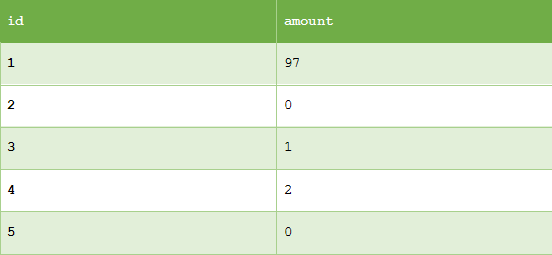
执行结果如下,并且性能也不错,在我本地测试只需要 1ms:
新的挑战
上述方案只得到一个最优解,从前文分析可知,5个海盗分金时有2个最优解,于是杨长老又出招了:"能否只用一句 SQL 获得所有的最优解?"有兴趣的小伙伴可以一起来挑战一下,欢迎微信交流!
资源下载
关注公众号:数据和云(OraNews)回复关键字获取
‘2017DTC’,2017 DTC 大会 PPT
‘DBALIFE’,“DBA 的一天”海报
‘DBA04’,DBA 手记4 经典篇章电子书
‘RACV1’, RAC 系列课程视频及 PPT
‘122ARCH’,Oracle 12.2 体系结构图
‘2017OOW’,Oracle OpenWorld 资料
‘PRELECTION’,大讲堂讲师课程资料