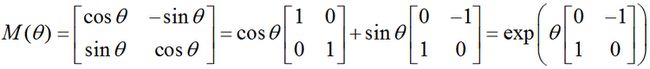矩阵特征分解介绍及雅克比(Jacobi)方法实现特征值和特征向量的求解(C++/OpenCV/Eigen)

对角矩阵(diagonal matrix)：只在主对角线上含有非零元素，其它位置都是零，对角线上的元素可以为0或其它值。形式上，矩阵D是对角矩阵，当且仅当对于所有的i≠j, D_i,j= 0. 单位矩阵就是对角矩阵，对角元素全部是1。我们用diag(v)表示一个对角元素由向量v中元素给定的对角方阵。对角矩阵受到关注的部分原因是对角矩阵的乘法计算很高效。计算乘法diag(v)x，我们只需要将x中的每个元素x_i放大v_i倍。换言之，diag(v)x = v⊙x。计算对角方阵的逆矩阵也很高效。对角方阵的逆矩阵存在，当且仅当对角元素都是非零值，在这种情况下，diag(v)^-1=diag([1/v₁, …, 1/v_n]^T)。在很多情况下，我们可以根据任意矩阵导出一些通用的机器学习算法；但通过将一些矩阵限制为对角矩阵，我们可以得到计算代价较低的(并且简明扼要的)算法。

不是所有的对角矩阵都是方阵。长方形的矩阵也有可能是对角矩阵。非方阵的对角矩阵没有逆矩阵，但我们仍然可以高效地计算它们的乘法。对于一个长方形对角矩阵D而言，乘法Dx会涉及到x中每个元素的缩放，如果D是瘦长型矩阵，那么在缩放后的末尾添加一些零；如果D是胖宽型矩阵，那么在缩放后去掉最后一些元素。

对角矩阵性质：

(1)、对角矩阵都是对称矩阵；

(2)、对角矩阵是上三角矩阵(对角线左下方的系数全部为零)及下三角矩阵(对角线右上方的系数全部为零)；

(3)、单位矩阵I_n及零矩阵(即所有元素皆为0的矩阵)恒为对角矩阵。一维的矩阵也恒为对角矩阵；

(4)、一个对角线上元素皆相等的对角矩阵是数乘矩阵，可表示为单位矩阵及一个系数λ的乘积：λI；

(5)、一对角矩阵diag(a1,…,an)的特征值为a1,…,an。而其特征向量为单位向量e1,…,en；

(6)、一对角矩阵diag(a1,…,an)的行列式为a1,…,an的乘积。

对称(symmetric)矩阵：在线性代数中，对称矩阵是一个方形矩阵，其转置矩阵和自身相等：A=A^T。

对称矩阵中的右上至左下方向元素以主对角线(左上至右下)为轴进行对称。若将其写作A=(a_ij)，则：a_ij=a_ji.

当某些不依赖参数顺序的双参数函数生成元素时，对称矩阵经常会出现。例如，如果A是一个距离度量矩阵，A_i,j表示i到点j的距离，那么A_i,j=A_j,i，因为距离函数是对称的。

对称矩阵特性：

(1)、对于任何方形矩阵X，X+X^T是对称矩阵；

(2)、A为方形矩阵是A为对称矩阵的必要条件；

(3)、对角矩阵都是对称矩阵；

(4)、两个对称矩阵的积是对称矩阵，当且仅当两者的乘法可交换。两个实对称矩阵乘法可交换当且仅当两者的特征空间相同；

(5)、如果X是对称矩阵，那么AXA^T也是对称矩阵。

单位向量(unit vector)是具有单位范数(unit norm)的向量：‖x‖₂=1.

如果x^Ty=0，那么向量x和向量y互相正交(orthogonal)。如果两个向量都有非零范数，那么这两个向量之间的夹角是90度。在Rⁿ中，至多有n个范数非零向量互相正交。如果这些向量不仅互相正交，并且范数都为1，那么我们称它们是标准正交(orthogonal)。

正交矩阵(orthogonal matrix)是指行向量和列向量是分别标准正交的方阵：A^TA=AA^T=I.这意味着A^-1=A^T.所以正交矩阵受到关注是因为求逆计算代价小。

正交是线性代数的概念，是垂直这一直观概念的推广。作为一个形容词，只有在一个确定的内积空间(内积空间是数学中线性代数里的基本概念，是增添了一个额外的结构的向量空间。这个额外的结构叫做内积或标量积。内积将一对向量与一个标量连接起来，允许我们严格地谈论向量的”夹角”和”长度”，并进一步讨论向量的正交性)中才有意义。若内积空间中两向量的内积为0，则称它们是正交的。如果能够定义向量间的夹角，则正交可以直观的理解为垂直。

标准正交基：在线性代数中，一个内积空间的正交基(orthogonal basis)是元素两两正交的基。称基中的元素为基向量。假若，一个正交基的基向量的模长都是单位长度1，则称这正交基为标准正交基或”规范正交基”(orthogonal basis)。

正交矩阵：在矩阵论中，正交矩阵(orthogonal matrix)是一个方块矩阵Q，其元素为实数，而且行与列皆为正交的单位向量，使得该矩阵的转置矩阵为其逆矩阵：Q^T=Q^-1ó Q^TQ=QQ^T=I.其中，I为单位矩阵。正交矩阵的行列式值必定为+1或-1。

旋转矩阵(Rotation matrix)：是在乘以一个向量的时候有改变向量的方向但不改变大小的效果并保持了手性的矩阵。旋转可分为主动旋转与被动旋转。主动旋转是指将向量逆时针围绕旋转轴所做出的旋转。被动旋转是对坐标轴本身进行的逆时针旋转，它相当于主动旋转的逆操作。

旋转矩阵性质：设M是任何维的一般旋转矩阵：M∈R^n*n

(1)、两个向量的点积(内积)在它们都被一个旋转矩阵操作之后保持不变：a·b=Ma·Mb；

(2)、从而得出旋转矩阵的逆矩阵是它的转置矩阵：MM^-1=MM^T=I 这里的I是单位矩阵；

(3)、一个矩阵是旋转矩阵，当且仅当它是正交矩阵并且它的行列式是单位一。正交矩阵的行列式是±1；则它包含了一个反射而不是真旋转矩阵；

(4)、旋转矩阵是正交矩阵，如果它的列向量形成Rⁿ的一个正交基，就是说在任何两个列向量之间的标量积是零(正交性)而每个列向量的大小是单位一(单位向量)；

在二维空间中，旋转可以用一个单一的角θ定义。作为约定，正角表示逆时针旋转。把笛卡尔坐标的列向量关于原点逆时针旋转θ的矩阵是：

特征分解(eigen decomposition)是使用最广的矩阵分解之一，即我们将矩阵分解成一组特征向量和特征值。

方阵A的特征向量(eigen vector)是指与A相乘后相当于对该向量进行缩放的非零向量v：Av=λv。标量λ被称为这个特征向量对应的特征值(eigenvalue)。(类似地，我们也可以定义左特征向量(left eigen vector) v^TA=λV^T，但是通常我们更关注右特征向量(right eigen vector))。

如果v是A的特征向量，那么任何缩放后的向量sv(s∈R,s≠0)也是A的特征向量。此外，sv和v有相同的特征值。基于这个原因，通常我们只考虑单位特征向量。

假设矩阵A有n个线性无关的特征向量{v⁽¹⁾,…,v⁽ⁿ⁾}，对应着特征值{λ₁,…,λ_n}。我们将特征向量连接成一个矩阵，使得每一列是一个特征向量：V=[v⁽¹⁾,…,v⁽ⁿ⁾].类似地，我们也可以将特征值连接成一个向量λ=[λ₁,…,λ_n]^T。因此A的特征分解(eigen decomposition)可以记作：A=Vdiag(λ)V^-1。

不是每一个矩阵都可以分解成特征值和特征向量。在某些情况下，特征分解存在，但是会涉及到复数，而非实数。每个实对称矩阵都可以分解成实特征向量和实特征值：A=QΛQ^T。其中Q是A的特征向量组成的正交矩阵，Λ是对角矩阵。特征值Λ_i,i对应的特征向量是矩阵Q的第i列，记作Q_:,i。因为Q是正交矩阵，我们可以将A看作是沿方向v⁽ⁱ⁾延展λ_i倍的空间。

虽然任意一个实对称矩阵A都有特征分解，但是特征分解可能并不唯一。如果两个或多个特征向量拥有相同的特征值，那么在由这些特征向量产生的生成子空间中，任意一组正交向量都是该特征值对应的特征向量。因此，我们可以等价地从这些特征向量中构成Q作为替代。按照惯例，我们通常按降序排列Λ的元素。在该约定下，特征分解唯一当且仅当所有的特征值都是唯一的。

矩阵的特征分解给了我们很多关于矩阵的有用信息。矩阵是奇异的当且仅当含有零特征值。实对称矩阵的特征分解也可以用于优化二次方程f(x)=x^TAx，其中限制‖x‖₂=1。当x等于A的某个特征向量时，f将返回对应的特征值。在限制条件下，函数f的最大值是最大特征值，最小值是最小特征值。

所有特征值都是正数的矩阵被称为正定(positive definite)；所有特征值都是非负数的矩阵被称为半正定(positive semidefinite)。同样地，所有特征值都是负数的矩阵被称为负定(negative definite)；所有特征值都是非正数的矩阵被称为半负定(negative semidefinite)。半正定矩阵受到关注是因为它们保证Ⅴx,x^TAx≥0。此外，正定矩阵还保证x^TAx=0 =>x=0。

特征分解：线性代数中，特征分解(Eigende composition)，又称谱分解(Spectral decomposition)是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。需要注意只有对可对角化矩阵(如果一个方块矩阵A相似于对角矩阵，也就是说，如果存在一个可逆矩阵P使得P^-1AP是对角矩阵，则它就被称为可对角化的)才可以施以特征分解。

特征值和特征向量：在数学上，特别是线性代数中，对于一个给定的线性变换(在数学中，线性映射(有的书上将”线性变换”作为其同义词，有的则不然)是在两个向量空间(包括由函数构成的抽象的向量空间)之间的一种保持向量加法和标量乘法的特殊映射。设V和W是在相同域K上的向量空间。法则f:V→W被称为是线性映射，如果对于V中任何两个向量x和y与K中任何标量a，满足下列两个条件：可加性：f(x+y)=f(x)+f(y)；齐次性：f(ax)=af(x)；这等价于要求对于任何向量x₁,…,x_m和标量a₁,…,a_m，方程f(a₁x₁+…+a_mx_m)=a₁f(x₁)+…+a_mf(x_m)成立)A，它的特征向量(eigen vector，也译固有向量或本征向量)v经过这个线性变换之后，得到的新向量与原来的v保持在同一条直线上，但其长度或方向也许会改变。即Av=λv，λ为标量，即特征向量的长度在该线性变换下缩放的比例，称λ为其特征值(本征值)。如果特征值为正，则表示v在经过线性变换的作用后方向也不变；如果特征值为负，说明方向会反转；如果特征值为0，则是表示缩回零点。但无论怎样，仍在同一条直线上。在一定条件下(如其矩阵形式为实对称矩阵的线性变换)，一个变换可以由其特征值和特征向量完全表述。

以上内容摘自 《深度学习中文版》 和 维基百科

通过雅克比(Jacobi)方法求实对称矩阵的特征值和特征向量操作步骤：S′=G^TSG,其中G是旋转矩阵，S′和S均为实对称矩阵，S′和S有相同的Frobenius norm，可以用一个最简单的3维实对称矩阵为例，根据公式进行详细推导(参考 维基百科 )：

通过旋转矩阵将对称矩阵转换为近似对角矩阵，进而求出特征值和特征向量，对角矩阵中主对角元素即为S近似的实特征值。Jacobi是通过迭代方法计算实对称矩阵的特征值和特征向量。

(1)、初始化特征向量V为单位矩阵；

(2)、初始化特征值eigenvalues为矩阵S主对角线元素；

(3)、将二维矩阵S赋值给一维向量A；

(4)、查找矩阵S中，每行除主对角元素外(仅上三角部分)绝对值最大的元素的索引赋给indR；

(5)、查找矩阵S中，第k列，前k个元素中绝对值最大的元素的索引赋给indC；

(6)、查找pivot的索引(k, l)，并获取向量A中绝对值最大的元素p；

(7)、如果p的绝对值小于设定的阈值则退出循环；

(8)、计算sinθ(s)和cosθ(c)的值；

(9)、更新(k, l)对应的A和eigenvalues的值；

(10)、旋转A的(k，l)；

(11)、旋转特征向量V的(k,l)；

(12)、重新计算indR和indC；

(13)、循环执行以上(6)~(12)步，直到达到最大迭代次数，OpenCV中设置迭代次数为n*n*30；

(14)、如果需要对特征向量和特性值进行sort，则执行sort操作。

以下是分别采用C++(参考opencv sources/modules/core/src/lapack.cpp)和OpenCV实现的求取实对称矩阵的特征值和特征向量：

#include "funset.hpp"
#include 
#include 
#include 
#include 
#include 
#include "common.hpp"

template
static inline _Tp hypot(_Tp a, _Tp b)
{
	a = std::abs(a);
	b = std::abs(b);
	if (a > b) {
		b /= a;
		return a*std::sqrt(1 + b*b);
	}
	if (b > 0) {
		a /= b;
		return b*std::sqrt(1 + a*a);
	}
	return 0;
}

template
int eigen(const std::vector>& mat, std::vector<_Tp>& eigenvalues, std::vector>& eigenvectors, bool sort_ = true)
{
	auto n = mat.size();
	for (const auto& m : mat) {
		if (m.size() != n) {
			fprintf(stderr, "mat must be square and it should be a real symmetric matrix\n");
			return -1;
		}
	}

	eigenvalues.resize(n, (_Tp)0);
	std::vector<_Tp> V(n*n, (_Tp)0);
	for (int i = 0; i < n; ++i) {
		V[n * i + i] = (_Tp)1;
		eigenvalues[i] = mat[i][i];
	}

	const _Tp eps = std::numeric_limits<_Tp>::epsilon();
	int maxIters{ (int)n * (int)n * 30 };
	_Tp mv{ (_Tp)0 };
	std::vector indR(n, 0), indC(n, 0);
	std::vector<_Tp> A;
	for (int i = 0; i < n; ++i) {
		A.insert(A.begin() + i * n, mat[i].begin(), mat[i].end());
	}

	for (int k = 0; k < n; ++k) {
		int m, i;
		if (k < n - 1) {
			for (m = k + 1, mv = std::abs(A[n*k + m]), i = k + 2; i < n; i++) {
				_Tp val = std::abs(A[n*k + i]);
				if (mv < val)
					mv = val, m = i;
			}
			indR[k] = m;
		}
		if (k > 0) {
			for (m = 0, mv = std::abs(A[k]), i = 1; i < k; i++) {
				_Tp val = std::abs(A[n*i + k]);
				if (mv < val)
					mv = val, m = i;
			}
			indC[k] = m;
		}
	}

	if (n > 1) for (int iters = 0; iters < maxIters; iters++) {
		int k, i, m;
		// find index (k,l) of pivot p
		for (k = 0, mv = std::abs(A[indR[0]]), i = 1; i < n - 1; i++) {
			_Tp val = std::abs(A[n*i + indR[i]]);
			if (mv < val)
				mv = val, k = i;
		}
		int l = indR[k];
		for (i = 1; i < n; i++) {
			_Tp val = std::abs(A[n*indC[i] + i]);
			if (mv < val)
				mv = val, k = indC[i], l = i;
		}

		_Tp p = A[n*k + l];
		if (std::abs(p) <= eps)
			break;
		_Tp y = (_Tp)((eigenvalues[l] - eigenvalues[k])*0.5);
		_Tp t = std::abs(y) + hypot(p, y);
		_Tp s = hypot(p, t);
		_Tp c = t / s;
		s = p / s; t = (p / t)*p;
		if (y < 0)
			s = -s, t = -t;
		A[n*k + l] = 0;

		eigenvalues[k] -= t;
		eigenvalues[l] += t;

		_Tp a0, b0;

#undef rotate
#define rotate(v0, v1) a0 = v0, b0 = v1, v0 = a0*c - b0*s, v1 = a0*s + b0*c

		// rotate rows and columns k and l
		for (i = 0; i < k; i++)
			rotate(A[n*i + k], A[n*i + l]);
		for (i = k + 1; i < l; i++)
			rotate(A[n*k + i], A[n*i + l]);
		for (i = l + 1; i < n; i++)
			rotate(A[n*k + i], A[n*l + i]);

		// rotate eigenvectors
		for (i = 0; i < n; i++)
			rotate(V[n*k+i], V[n*l+i]);

#undef rotate

		for (int j = 0; j < 2; j++) {
			int idx = j == 0 ? k : l;
			if (idx < n - 1) {
				for (m = idx + 1, mv = std::abs(A[n*idx + m]), i = idx + 2; i < n; i++) {
					_Tp val = std::abs(A[n*idx + i]);
					if (mv < val)
						mv = val, m = i;
				}
				indR[idx] = m;
			}
			if (idx > 0) {
				for (m = 0, mv = std::abs(A[idx]), i = 1; i < idx; i++) {
					_Tp val = std::abs(A[n*i + idx]);
					if (mv < val)
						mv = val, m = i;
				}
				indC[idx] = m;
			}
		}
	}

	// sort eigenvalues & eigenvectors
	if (sort_) {
		for (int k = 0; k < n - 1; k++) {
			int m = k;
			for (int i = k + 1; i < n; i++) {
				if (eigenvalues[m] < eigenvalues[i])
					m = i;
			}
			if (k != m) {
				std::swap(eigenvalues[m], eigenvalues[k]);
				for (int i = 0; i < n; i++)
					std::swap(V[n*m+i], V[n*k+i]);
			}
		}
	}

	eigenvectors.resize(n);
	for (int i = 0; i < n; ++i) {
		eigenvectors[i].resize(n);
		eigenvectors[i].assign(V.begin() + i * n, V.begin() + i * n + n);
	}

	return 0;
}

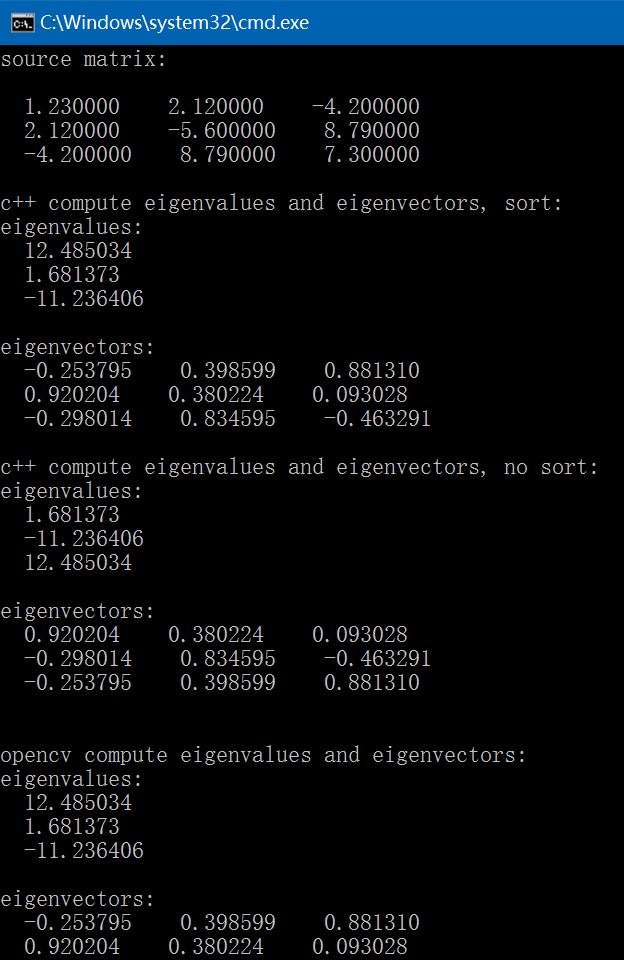
int test_eigenvalues_eigenvectors()
{
	std::vector vec{ 1.23f, 2.12f, -4.2f,
		2.12f, -5.6f, 8.79f,
		-4.2f, 8.79f, 7.3f };
	const int N{ 3 };

	fprintf(stderr, "source matrix:\n");
	int count{ 0 };
	for (const auto& value : vec) {
		if (count++ % N == 0) fprintf(stderr, "\n");
		fprintf(stderr, "  %f  ", value);
	}
	fprintf(stderr, "\n\n");

	fprintf(stderr, "c++ compute eigenvalues and eigenvectors, sort:\n");
	std::vector> eigen_vectors1, mat1;
	std::vector eigen_values1;
	mat1.resize(N);
	for (int i = 0; i < N; ++i) {
		mat1[i].resize(N);
		for (int j = 0; j < N; ++j) {
			mat1[i][j] = vec[i * N + j];
		}
	}

	if (eigen(mat1, eigen_values1, eigen_vectors1, true) != 0) {
		fprintf(stderr, "campute eigenvalues and eigenvector fail\n");
		return -1;
	}

	fprintf(stderr, "eigenvalues:\n");
	std::vector> tmp(N);
	for (int i = 0; i < N; ++i) {
		tmp[i].resize(1);
		tmp[i][0] = eigen_values1[i];
	}
	print_matrix(tmp);

	fprintf(stderr, "eigenvectors:\n");
	print_matrix(eigen_vectors1);

	fprintf(stderr, "c++ compute eigenvalues and eigenvectors, no sort:\n");
	if (eigen(mat1, eigen_values1, eigen_vectors1, false) != 0) {
		fprintf(stderr, "campute eigenvalues and eigenvector fail\n");
		return -1;
	}

	fprintf(stderr, "eigenvalues:\n");
	for (int i = 0; i < N; ++i) {
		tmp[i][0] = eigen_values1[i];
	}
	print_matrix(tmp);

	fprintf(stderr, "eigenvectors:\n");
	print_matrix(eigen_vectors1);

	fprintf(stderr, "\nopencv compute eigenvalues and eigenvectors:\n");
	cv::Mat mat2(N, N, CV_32FC1, vec.data());

	cv::Mat eigen_values2, eigen_vectors2;
	bool ret = cv::eigen(mat2, eigen_values2, eigen_vectors2);
	if (!ret) {
		fprintf(stderr, "fail to run cv::eigen\n");
		return -1;
	}

	fprintf(stderr, "eigenvalues:\n");
	print_matrix(eigen_values2);

	fprintf(stderr, "eigenvectors:\n");
	print_matrix(eigen_vectors2);

	return 0;
}

执行结果如下：

以下是采用Eigen实现的求取特征值和特征向量的code：

#include "funset.hpp"
#include 
#include 
#include 
#include 
#include 
#include 
#include "common.hpp"

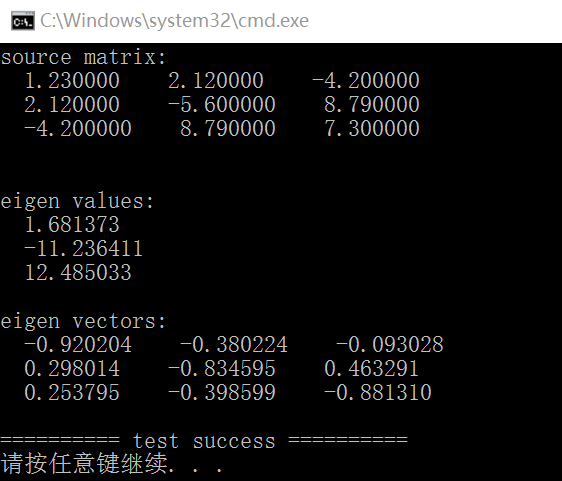
int test_eigenvalues_eigenvectors()
{
	std::vector vec{ 1.23f, 2.12f, -4.2f,
		2.12f, -5.6f, 8.79f,
		-4.2f, 8.79f, 7.3f };
	const int N{ 3 };

	fprintf(stderr, "source matrix:\n");
	print_matrix(vec.data(), N, N);
	fprintf(stderr, "\n");

	Eigen::Map m(vec.data(), N, N);

	Eigen::EigenSolver es(m);
	Eigen::VectorXf eigen_values = es.eigenvalues().real();
	fprintf(stderr, "eigen values:\n");
	print_matrix(eigen_values.data(), N, 1);
	Eigen::MatrixXf eigen_vectors = es.eigenvectors().real();
	fprintf(stderr, "eigen vectors:\n");
	print_matrix(eigen_vectors.data(), N, N);

	return 0;
}

执行结果如下：

由以上结果可见：C++、OpenCV、Eigen结果是一致的。

GitHub：

https://github.com/fengbingchun/NN_Test

https://github.com/fengbingchun/Eigen_Test