基于fisher线性判别法的分类器设计

0.引言说明
这篇文章实际上是楼主上的模式识别课程的课堂报告，楼主偷懒把东西直接贴出来了。选择fisher判别法的原因主要是想学习一下这个方法，这个方法属于线性判别法，操作起来和lda判别法近乎没啥区别。

在选用这个方法之前，楼主也尝试过用其它方法，包括knn（自己也写了个）、svm（不会实现）。讲道理，老师给的数据太坑爹了，好几类都不能用线性判别来区分，必须用非线性分类器，当然这是我在设计完本分类器后，通过实验得到的结论。提交这个报告之后，我也尝试用势函数法来实现，这玩意和感知器有点类似，但是感知器也只用于线性判别，势函数法的优点在于可以针对非线性数据判别，并能保证判决函数的收敛。但是，这种需要遍历每一条数据的方法，效率真是惨不仍睹，跑了4个多小时都没办法跑出2类的分类结果。

写这篇文章的目的主要还是帮助楼主自己记忆（拥有鱼的记忆的人真是伤不起啊，几秒前做的事都可以忘掉），后面一篇文章会记下楼主尝试其他方案的算法原理。

推荐参考书籍：1.《现代模式识别（第二版）》孙即祥 著 楼主用的方法在这本书上都有十分详细的介绍
　　　　　　　2.《Pattern Recognition and Machine Learning》 Christopher Bishop 著 经典书籍，外国佬写东西都很认真，看中文书有啥不懂的，这上面应该都有讲解
　　　　　　　3.《模式识别与智能计算的MATLAB实现》 各种算法的matlab源码，都懂的

1.问题描述
现有实验数据“train_data.mat”，其基本说明如下：
1、9类数据，分别为C1~C9；
2、数据组织：特征维数*样本数量；
3、每个样本特征维数为103。
对此实验数据选择一种方法设计分类器，要求有较高的分类精度，并对实验结果进行评价和分析。

2.方法选择
Fisher准则的基本原理：找到一个最合适的投影轴，使两类样本在该轴上投影之间的距离尽可能远，而每一类样本的投影尽可能紧凑，从而使分类效果为最佳。
下面是Fisher准则判决的图例：
　　　　　　　　　
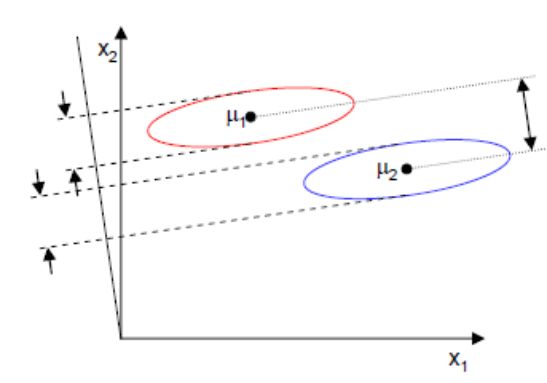
可以看到，投影后的数据可以保证两类区分度最大，每一类数据也更加密集。Fisher准则依靠的是数据的统计均值和离散度的函数作为判别优势的标准，其具体计算公式如下：
类内离散度矩阵公式为：
　　　　　　　　　　　
总类内离散度矩阵公式为：
　　　　　　　　　　　
类间离散度矩阵公式为：
　　　　　　　　　　　
其中，mi为第i类的样本均值。
为保证投影后的类间差异最大，类内聚合度最高，则有如下准则函数的定义：
　　　　　　　　　　　
使上式达到最大，则得到投影矢量的解为：
　　　　　　　　　　　
判决函数的阈值可以选为两类投影中心的均值或者是加权均值。

Fisher投影准则属于线性判别准则，线性判别准则存在以下几点限制：
a.不适合对非高斯分布样本进行降维，如下图示例
　　　　　　　　
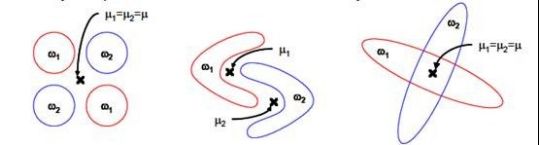
b.过度依赖均值信息
c.存在过度拟合的可能性
……

3.算法设计
由于一般的fisher算法只适用于两类分析，对多类的分析可以采用两种方式：一种是采用lda（Linear discriminant analysis）算法设计一个针对多类的分类器，其原理与适用性和fisher算法近乎完全一样；另一种是，对k类待实验数据，两两训练一个线性判别分类器，让每个分类器进行投票来判决类别，一共需要设计n=k*(k-1)/2个分类器。本文采用后者，针对本文使用到的9类实验数据，一共需要设计36个分类器。如下是整个算法的流程图：
　　　　　　　
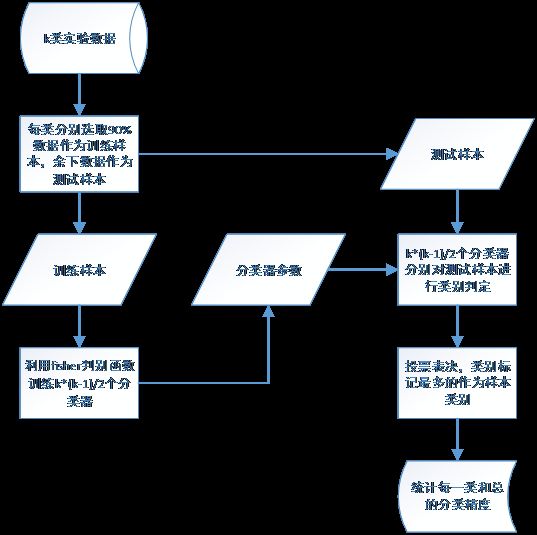
多类别fisher分类器流程图
由于每类两两之间均会有一个分类器，也就是说，对某一个测试样本进行投票表决时，每类最多可以获得8票（此时，其它类别可以获得的最多票数为7），那么36个分类器如果均有较高的分类精度时，整体的分类精度也会很高。

4.实验结果分析
实验一：对实验数据集“train_data.mat”中的每一类抽取30%作为训练样本，余下的70%全部作为测试样本。
运行时间：2s左右
　　　　　
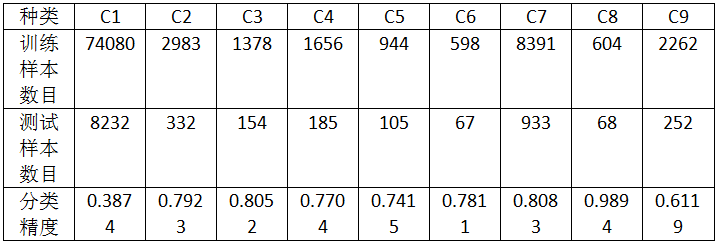
总分类精度：0.4670
由上面的结果可以知道，在运行时间上分析，本算法的运行速度很快；在计算结果上分析，除第一类和第九类测试数据的分类精度较差之外，其它类的分类精度均较好。
但第一类测试数据的分类精度太糟糕，而且其测试样本的数量占比很大，导致总的分类精度也很糟糕。初步猜想是，第一类数据分布类型并不适用于线性判别分类器。下面，我进行了3组实验来验证这一猜想。
实验二：每类选择30%作为训练样本，选取200个作为测试样本
　　　　　
总分类精度：0.7411
该实验说明了，实验一总分类精度糟糕的原因是，具有糟糕分类精度的第一类数据选取的测试样本过多。

实验三：每类选择600个作为训练样本，选取70%作为测试样本
　　　　　
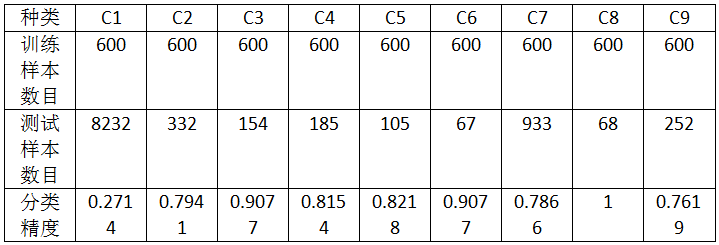
总分类精度：0.3803
考虑到分类结果和训练的样本量有关，实验一中参与训练的第一类样本数据过多，可能对分类器有较大影响，所以进行了实验三。但从实验结果可以发现，每一类的分类精度有升有降，分类精度降低是由于训练样本数量减少导致的，而部分类别的分类精度上升可能是由于第一类参与训练的类别减少而导致。

实验四：除去C1类，每类选择30%作为训练样本，选取70%作为测试样本
　　　　　
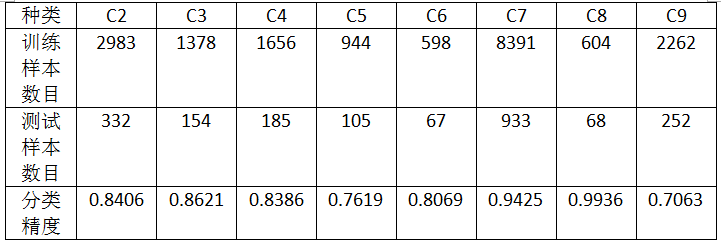
总分类精度：0.8712
实验四将第一类去除，选取剩下的8类进行分类，此时共有28个fisher分类器。从实验结果可以看到，8类的分类精度大部分都有所提升。

下面将第一类和其它类训练后训练样本数据的投影结果显示出来，选择与第一类有关的8个分类器：
　　　　　 　　　C1和C2训练样本投影结果 　　　　　　　　　　　C1和C3训练样本投影结果
　　　　　　　　　　
　　　　　
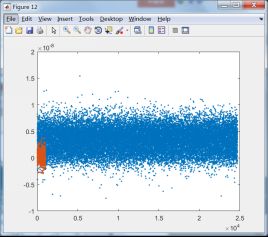
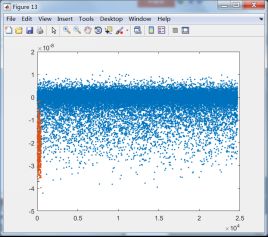
　　　　　 　　　C1和C4训练样本投影结果 　　　　　　　　　　　C1和C5训练样本投影结果
　　　　　　　　　　
　　　　　
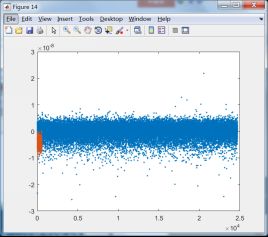
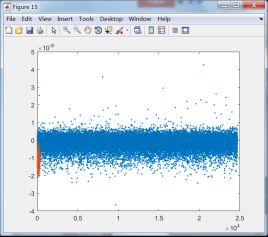
　　　　　　　　 C1和C6训练样本投影结果 　　　　　　　　　　　C1和C7训练样本投影结果
　　　　　　　　　　
　　　　　
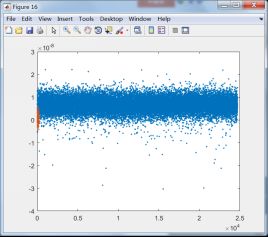
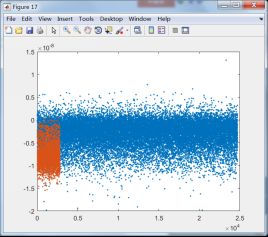
　　　　　 　　　C1和C8训练样本投影结果 　　　　　　　　　　　C1和C9训练样本投影结果
　　　　　　　　　　
　　　　　
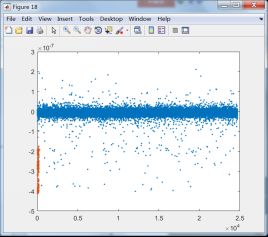
由上面的投影结果可以发现，除第8类外，其它7类均无法与第1类区分开来，由此可知，fisher线性判别法无法适用于第1类这样的数据。结合线性判别的适用性可知，第一类数据的分布可能并非类球形分布，或者说第一类数据包含了其它除第8类数据外的所有类别。

附录：

%训练分类器
function [w,F] = myfisher(m1,m2,i,j)
    m1 = m1';
    m2 = m2';
    [nm1,~] = size(m1);
    [nm2,~] = size(m2);
    u1=mean(m1);%求均值
    u2=mean(m2);
    % 计算类内散度Si和总类内散度Sw
    One1=ones(nm1,1);
    One2=ones(nm2,1);
    S1=nm1*(m1-One1*u1)'*(m1-One1*u1);
    S2=nm2*(m2-One2*u2)'*(m2-One2*u2);
    Sw=(S1+S2)/2;
%     Sw=(nm1*S1+nm2*S2)/(nm1+nm2); %调整
    %变换向量
    w=Sw\(u1-u2)';
%     F = w'*((nm1*u1+nm2*u2)/(nm1+nm2))';
    F = w'*((u1+u2)/2)';
%     y1 = w'*m1';
%     y2 = w'*m2';
%     figure(i*10+j);
%     plot(y1,'.');
%     hold on
%     plot(y2,'.');
%     std1 = std(y1);
%     std2 = std(y2);
%     F = w'*((std2*u1+std1*u2)/(std1+std2))';
end

%测试样本类别判断
function res = myfisher_distin(m1,fisher,inte)
    [~,m] = size(m1);
    res = zeros(inte,m);
    for i = 1:inte
        w = fisher.w{1,i};
        F = fisher.F{1,i};
        c = fisher.c{1,i};
        yt = w'*m1;
        res1 = zeros(size(yt));
        res1(yt>F) = c(1);
        res1(yt2);
        res(i,:) = res1;
    end
    if(inte>1)
        res = mode(res);
    end
end

---

参考：1.http://blog.csdn.net/ffeng271/article/details/7353834
　　　2.《现代模式识别（第二版）》孙即祥 著