多元线性模型中共线性产生的原因解析

      在很多书籍中谈到了共线性问题，作为多元统计中基本假设之一，却经常被违背，影响模型稳定性和统计power。在不少的论文中谈到了，国内的很多书籍往往一笔带过。因为，属于统计计算领域内容，非专业人士，也鲜有能明白其中内涵，现依据手上的一些资料和自己的理解，写就一些。

一.共线性概念

        共线性问题(collinearity)，是指两个或者更多的自变量高度相关，当只有两个高度相关的时候，我们通过相关系数矩阵就可以看出来。但是两个以上的自变量存在相关的时候就无法通过查看两两相关系数矩阵，这时候对共线性测量用VIF （方差膨胀因子），这种情况叫做多重共线性（mulitcollinearity）。VIF 是拟合全模型时的系数矩阵B的方差除以单变量回归中B 的方差所得比例，VIF最小可能是1，表示完全不存在共线性，通常情况下，总是有少数自变量之间存在一定程度的共线性，一般经验法则是，当VIF超过5或者10就表示有共线性问题存在。

用数学语言描述是：

        通俗的解释就是某一个变量，可以近似的有另一个变量线性表达时，存在完全共线性，如a1= 1.5 * a2，此时就是完全共线性了。什么时候会出现这样的问题呢，当纳入的自变量是婴儿的头围和体重的时候，两个变量的相关可能是1或者-1的时候。当然，变量存在误差，所以说，上面的等式中，误差无限趋于0时，共线性越严重。

二. 共线性问题导致的问题

        上文交代了背景和概念，我们先来看看，在前面说的影响模型的稳定性和统计效力的问题。也就是计算的误差很大且不稳定。

上图表明：（1）自变量信用额度和年龄没有明显的关系；（2）信用额度和信用评级由很高的相关性，则两个自变量是共线的（collinear）。

           下面这张图表示了共线性可能导致的问题，左侧是余额对年龄，额度的不同回归系数的估计

residual sum of squares(RSS 残差平方和)等高线图，每个椭圆代表相同的RSS对应的一组估计系数，接近椭圆中心，则RSS值越低，图中的红点，代表令RSS最小的系数估计，就是通过最小二乘（Least Squares , LS）我们要最终得到的极小值。

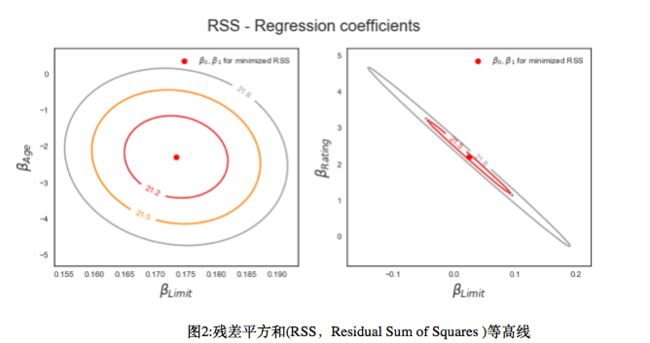
RSS等高线得两个估计系数的变化如图所示。如果上面这个图不是很明显，那么，重新画一幅。

                    图3：二维残差平方和等高线

图3更加明显的可视化了由于高度共线性的存在，使得估计过程无法分摊两个自变量对因变量的贡献。    

    由于无法通过解析式求解复杂的模型，所以用数值（近似）计算求解参数，广为人知的迭代法，不断迭代减少二者之间的距离。上面两幅图就是显示在迭代运算过程中的求解过程。

    如果等高线呈一条狭窄的山谷，很多系数估计值有同样的RSS值，数据微小的变化可能导致使RSS减小的系数估计沿着这条山谷的任何方向移动，系数估计就存在很大的不确定性，很大的改变，用统计语言描述就是波动大，也就是这组系数的方差大。我们对系数检验使用的是t检验的话，$$t=\frac{\beta }{SE}$$,标准误的增大，我们可能无法拒绝,意味着假设检验的效力（Power）被共线性减小了，使得更容易拒绝原假设。

三.稳定性的度量

       我们解释了误差大不稳定这个疑问，但是，如何度量估计过程是否稳定呢。

线性方程组求解的稳定性，设 Ax=b为n阶方阵存在唯一解的充分必要条件是A为满秩矩阵，即A的列向量的任何一个非零线性组合都不等于零向量，如果A十分接近于零向量，则此时误差很大且不稳定。（此时的Ax,是没有截距的多元线性模型，b是因变量），呼应了前面讲的共线性问题。

当A为满秩矩阵时，$$x=A^{-1}b,A^{-1}Ax=A^{-1}b$$

需要注意的是，我们在使用普通最小二乘的时候假设因变量存在误差，于是设输入的误差为$$b+\Delta b$$

b输入的误差(扰动)在矩阵A稳定不变时，造成的精确的解向量x变成$$x+\Delta x$$

于是公式改写成$$A(x+\Delta x)=b+\Delta b$$

$$\Delta x 满足，\frac{||\Delta x||_{2}}{||x||_{2}}\leq (||A||_{2}||A^{-1}||_{2})\frac{||\Delta b||_{2}}{||b||_{2}}$$

其中，$$||A||_{2}||A^{-1}||_{2},就是条件数，记为K_{p}(A)$$ 

用条件数用来衡量以A为系数矩阵的线性求解的稳定性。详见这里

四.解决办法

        上面就从统计的角度讲解了关于共线性的问题，那么，结果共线性问题有哪些办法呢？

从最简单的开始。

[1] 删除法（针对两两高相关的共线性）

        对于两个高度相关的变量，可以通过两两之间的相关系数来判断，比如，设定一个阈值，对于大于0.75相关系数的变量进行删除，

步骤：

1.计算自变量的相关系数矩阵

2.找出相关系数的绝对值最小的那对自变量a1,a2

3.计算a1与其他自变量相关系数的均值，对a2也做同样的计算

4.如果a1的平均相关系数更大，则将a1移除，否则移除a2。

重复2—4,直到所有的相关系数绝对值都低于设定的阈值。

        通过移除两两相关的自变量，将会减少预测变量的个数，同时，可能依然无法完全消除共线性，这是因为某些两个以上的自变量存在共线性，也就是多重共线性。

      上文讲了可以用VIF来诊断两个以上的变量存在的多重共线性，VIF的局限性又是什么呢？VIF诊断是基于线性模型的，而且要求样本量比自（预测）变量数多，同时，虽然能够判断共线性，但是并不能决定应该删除那些变量开减轻共线性问题。

[2] 特征提取，压缩回归系数方法类

        除了通过删除变量，还可以通过特征提取技术（主成分分析， 偏最小二乘法，岭回归， LASSO等，因为此几种方法论文中讲解的很多，不再累赘）缓解自变量之间的强相关，对模型的影响。然而这些方法使得自变量与因变量之间的联系更加复杂，解释起来也更加困难，也不能够保证得到的自变量与因变量关系的模型一定有联系。

[3] 逐步回归方法

        逐步回归也能在一定程度上减轻共线性。逐步回归分析方法是综合了逐步剔除法和逐步引入法的特点产生的方法。其基本原理为: 从一个自变量出发, 视自变量对因变量的影响显著性大小, 从大到小引入回归方程, 同时,在逐个自变量选入回归方程中, 如果发现先前被引入的自变量在其后由于某些自变量的引入而失去其重要性, 可以从回归方程中随时予以剔除。引入一个变量或剔除一个变量, 为逐步回归的一步, 每步都要进行显著性检验, 以便保证每次引入变量前回归方程中只包括显著性检验, 这个过程反复进行, 直到既无不显著变量从方程中剔除, 又无显著性变量需要引入回归方程为止。   数据中高度相关的变量增加了模型的复杂度而非信息量，在获取变量的成本（时间，金钱）很高的情况下，变量的数目越少越好。

 [4] 增加样本

         事实上我们也可以用点估计的知识来解释，良好点估计的统计量必须具备一定的前提条件，1.无偏性，2.一致性，3.有效性。一致性：总体参数的估计量随着样本容量的无限增大，越来越接近它所顾及的总体参数，即总体均数和标准差，也就理解了增大样本做法有其统计学意义上的合理性，同时我们看到上面的公式，增加样本事实上也是让A列向量的线性组合更加不容易等于一个零向量,也是缓解避免了完全共线性问题的发生。

五.总结

        使用高相关的自变量带来数学上的麻烦，引起模型估计结果极不稳定，导致数值计算的错误，弱化模型的预测能力。共线性问题看起来是一个人人都懂，却有人人都说不清所以然的问题，该问题是一个交叉与统计学和计算机科学，还需要有线性代数的基础，是一个牵连很多其他知识点，比如，矩阵行变换，特征值，奇异值分解，正则化收缩估计。（线性代数号称是21世界的高等数学，感谢当初大学老师威胁着要把你们都挂了）因此，要彻底地解决共线性问题，就要合理地分离这部分重叠的信息，我个人也以为“解决多重共线性本质就是要合理分配变量间的交互作用的影响”(详见这里)。上文讲到的诸多方法，恰恰说明了，此问题并没有一个定论还需要针对不同的数据不同的场景，依据研究者自身的需求来选择合理的方法。到底是关注预测还是关注解释，简单高效还是倾向于复杂有效，对p值的不屑还是孜孜不倦，不一而足。大数据的到来，许多研究范式也在变化。所用材料是手头上刚好有的，基于目前的理解和掌握，未免还有更加具有说服力的资料可以用来补充。也依然不断的提升“统计成熟度”。

参考文献

1.加雷斯·詹姆斯, GarethJames, 詹姆斯,等. 统计学习导论[M]. 机械工业出版社, 2015.

2.统计计算/李东风编，北京：高等教育出版社，2017.3

3.张贤达. 矩阵分析与应用.第2版[M]. 清华大学出版社, 2013.

4.马克思·库恩, 谢尔·约翰逊, MaxKuhn,等. 应用预测建模[M]. 机械工业出版社, 2016.

5.贾巧萍. 相对重要性在处理多重共线性中的应用[D]. 云南财经大学, 2012.

6.满敬銮, 杨薇. 基于多重共线性的处理方法[J]. 数学理论与应用, 2010(2):105-109.

 ps: 参考文献中的1和4是有英文原版的，都是Springer出版社出版的经典黄皮书，同时国内对于这个问题有详细讲解的是，

王惠文著《偏最小二乘回归方法与应用》和张启锐著《实用回归方法》