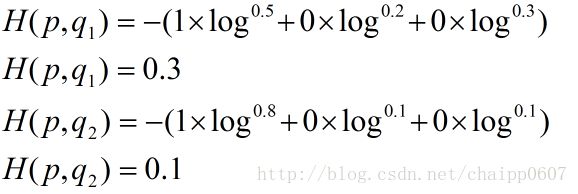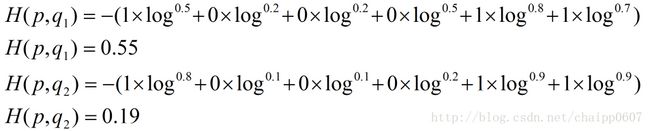简单的交叉熵损失函数
说起交叉熵损失函数「Cross Entropy Loss」,脑海中立马浮现出它的公式:
L=−[ylog y^+(1−y)log (1−y^)]L=−[ylog y^+(1−y)log (1−y^)]
我们已经对这个交叉熵函数非常熟悉,大多数情况下都是直接拿来使用就好。但是它是怎么来的?为什么它能表征真实样本标签和预测概率之间的差值?上面的交叉熵函数是否有其它变种?也许很多朋友还不是很清楚!没关系,接下来我将尽可能以最通俗的语言回答上面这几个问题。
1. 交叉熵损失函数的数学原理
我们知道,在二分类问题模型:例如逻辑回归「Logistic Regression」、神经网络「Neural Network」等,真实样本的标签为 [0,1],分别表示负类和正类。模型的最后通常会经过一个 Sigmoid 函数,输出一个概率值,这个概率值反映了预测为正类的可能性:概率越大,可能性越大。
Sigmoid 函数的表达式和图形如下所示:
g(s)=11+e−sg(s)=11+e−s
其中 s 是模型上一层的输出,Sigmoid 函数有这样的特点:s = 0 时,g(s) = 0.5;s >> 0 时, g ≈ 1,s << 0 时,g ≈ 0。显然,g(s) 将前一级的线性输出映射到 [0,1] 之间的数值概率上。这里的 g(s) 就是交叉熵公式中的模型预测输出 。
我们说了,预测输出即 Sigmoid 函数的输出表征了当前样本标签为 1 的概率:
y^=P(y=1|x)y^=P(y=1|x)
很明显,当前样本标签为 0 的概率就可以表达成:
1−y^=P(y=0|x)1−y^=P(y=0|x)
重点来了,如果我们从极大似然性的角度出发,把上面两种情况整合到一起:
P(y|x)=y^y⋅(1−y^)1−yP(y|x)=y^y⋅(1−y^)1−y
不懂极大似然估计也没关系。我们可以这么来看:
当真实样本标签 y = 0 时,上面式子第一项就为 1,概率等式转化为:
P(y=0|x)=1−y^P(y=0|x)=1−y^
当真实样本标签 y = 1 时,上面式子第二项就为 1,概率等式转化为:
P(y=1|x)=y^P(y=1|x)=y^
两种情况下概率表达式跟之前的完全一致,只不过我们把两种情况整合在一起了。
重点看一下整合之后的概率表达式,我们希望的是概率 P(y|x) 越大越好。首先,我们对 P(y|x) 引入 log 函数,因为 log 运算并不会影响函数本身的单调性。则有:
log P(y|x)=log(y^y⋅(1−y^)1−y)=ylog y^+(1−y)log(1−y^)log P(y|x)=log(y^y⋅(1−y^)1−y)=ylog y^+(1−y)log(1−y^)
我们希望 log P(y|x) 越大越好,反过来,只要 log P(y|x) 的负值 -log P(y|x) 越小就行了。那我们就可以引入损失函数,且令 Loss = -log P(y|x)即可。则得到损失函数为:
L=−[ylog y^+(1−y)log (1−y^)]L=−[ylog y^+(1−y)log (1−y^)]
非常简单,我们已经推导出了单个样本的损失函数,是如果是计算 N 个样本的总的损失函数,只要将 N 个 Loss 叠加起来就可以了:
L=∑i=1Ny(i)log y^(i)+(1−y(i))log (1−y^(i))L=∑i=1Ny(i)log y^(i)+(1−y(i))log (1−y^(i))
这样,我们已经完整地实现了交叉熵损失函数的推导过程。
2. 交叉熵损失函数的直观理解
可能会有读者说,我已经知道了交叉熵损失函数的推导过程。但是能不能从更直观的角度去理解这个表达式呢?而不是仅仅记住这个公式。好问题!接下来,我们从图形的角度,分析交叉熵函数,加深大家的理解。
首先,还是写出单个样本的交叉熵损失函数:
L=−[ylog y^+(1−y)log (1−y^)]L=−[ylog y^+(1−y)log (1−y^)]
我们知道,当 y = 1 时:
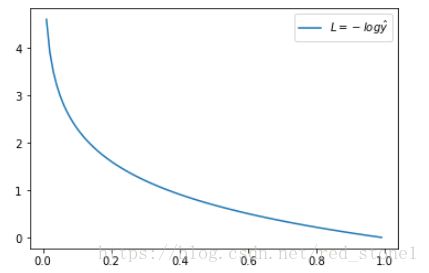
L=−log y^L=−log y^
这时候,L 与预测输出的关系如下图所示:
看了 L 的图形,简单明了!横坐标是预测输出,纵坐标是交叉熵损失函数 L。显然,预测输出越接近真实样本标签 1,损失函数 L 越小;预测输出越接近 0,L 越大。因此,函数的变化趋势完全符合实际需要的情况。
当 y = 0 时:
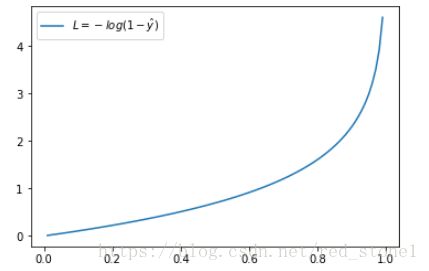
L=−log (1−y^)L=−log (1−y^)
这时候,L 与预测输出的关系如下图所示:
同样,预测输出越接近真实样本标签 0,损失函数 L 越小;预测函数越接近 1,L 越大。函数的变化趋势也完全符合实际需要的情况。
从上面两种图,可以帮助我们对交叉熵损失函数有更直观的理解。无论真实样本标签 y 是 0 还是 1,L 都表征了预测输出与 y 的差距。
另外,重点提一点的是,从图形中我们可以发现:预测输出与 y 差得越多,L 的值越大,也就是说对当前模型的 “ 惩罚 ” 越大,而且是非线性增大,是一种类似指数增长的级别。这是由 log 函数本身的特性所决定的。这样的好处是模型会倾向于让预测输出更接近真实样本标签 y。
3. 交叉熵损失函数的其它形式
什么?交叉熵损失函数还有其它形式?没错!我刚才介绍的是一个典型的形式。接下来我将从另一个角度推导新的交叉熵损失函数。
这种形式下假设真实样本的标签为 +1 和 -1,分别表示正类和负类。有个已知的知识点是Sigmoid 函数具有如下性质:
1−g(s)=g(−s)1−g(s)=g(−s)
这个性质我们先放在这,待会有用。
好了,我们之前说了 y = +1 时,下列等式成立:
P(y=+1|x)=g(s)P(y=+1|x)=g(s)
如果 y = -1 时,并引入 Sigmoid 函数的性质,下列等式成立:
P(y=−1|x)=1−g(s)=g(−s)P(y=−1|x)=1−g(s)=g(−s)
重点来了,因为 y 取值为 +1 或 -1,可以把 y 值带入,将上面两个式子整合到一起:
P(y|x)=g(ys)P(y|x)=g(ys)
这个比较好理解,分别令 y = +1 和 y = -1 就能得到上面两个式子。
接下来,同样引入 log 函数,得到:
log P(y|x)=log g(ys)log P(y|x)=log g(ys)
要让概率最大,反过来,只要其负数最小即可。那么就可以定义相应的损失函数为:
L=−logg(ys)L=−logg(ys)
还记得 Sigmoid 函数的表达式吧?将 g(ys) 带入:
L=−log11+e−ys=log (1+e−ys)L=−log11+e−ys=log (1+e−ys)
好咯,L 就是我要推导的交叉熵损失函数。如果是 N 个样本,其交叉熵损失函数为:
L=∑i=1Nlog (1+e−ys)L=∑i=1Nlog (1+e−ys)
接下来,我们从图形化直观角度来看。当 y = +1 时:
L=log (1+e−s)L=log (1+e−s)
这时候,L 与上一层得分函数 s 的关系如下图所示:
横坐标是 s,纵坐标是 L。显然,s 越接近真实样本标签 1,损失函数 L 越小;s 越接近 -1,L 越大。
另一方面,当 y = -1 时:
L=log(1+es)L=log(1+es)
这时候,L 与上一层得分函数 s 的关系如下图所示:
同样,s 越接近真实样本标签 -1,损失函数 L 越小;s 越接近 +1,L 越大。
4. 总结
本文主要介绍了交叉熵损失函数的数学原理和推导过程,也从不同角度介绍了交叉熵损失函数的两种形式。第一种形式在实际应用中更加常见,例如神经网络等复杂模型;第二种多用于简单的逻辑回归模型。
交叉熵的作用
通过神经网络解决多分类问题时,最常用的一种方式就是在最后一层设置n个输出节点,无论在浅层神经网络还是在CNN中都是如此,比如,在AlexNet中最后的输出层有1000个节点: 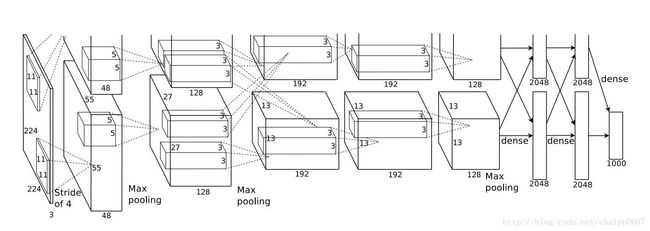
而即便是ResNet取消了全连接层,也会在最后有一个1000个节点的输出层: 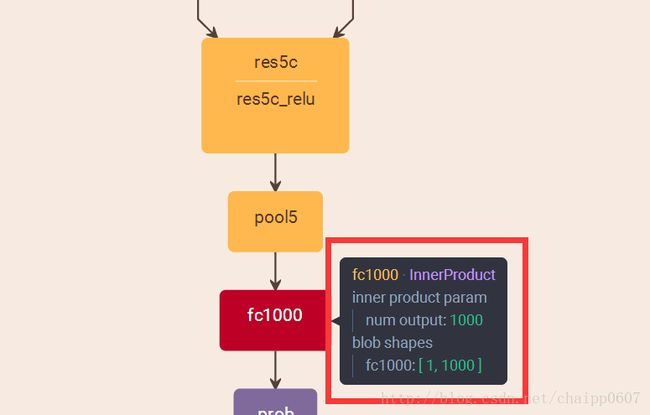
一般情况下,最后一个输出层的节点个数与分类任务的目标数相等。假设最后的节点数为N,那么对于每一个样例,神经网络可以得到一个N维的数组作为输出结果,数组中每一个维度会对应一个类别。在最理想的情况下,如果一个样本属于k,那么这个类别所对应的的输出节点的输出值应该为1,而其他节点的输出都为0,即[0,0,1,0,….0,0],这个数组也就是样本的Label,是神经网络最期望的输出结果,交叉熵就是用来判定实际的输出与期望的输出的接近程度!
Softmax回归处理
神经网络的原始输出不是一个概率值,实质上只是输入的数值做了复杂的加权和与非线性处理之后的一个值而已,那么如何将这个输出变为概率分布?
这就是Softmax层的作用,假设神经网络的原始输出为y1,y2,….,yn,那么经过Softmax回归处理之后的输出为: 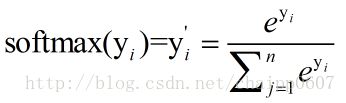
很显然的是: 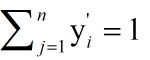
而单个节点的输出变成的一个概率值,经过Softmax处理后结果作为神经网络最后的输出。
交叉熵的原理
交叉熵刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出,概率分布q为实际输出,H(p,q)为交叉熵,则:
这个公式如何表征距离呢,举个例子:
假设N=3,期望输出为p=(1,0,0),实际输出q1=(0.5,0.2,0.3),q2=(0.8,0.1,0.1),那么:
很显然,q2与p更为接近,它的交叉熵也更小。
除此之外,交叉熵还有另一种表达形式,还是使用上面的假设条件:
其结果为:
以上的所有说明针对的都是单个样例的情况,而在实际的使用训练过程中,数据往往是组合成为一个batch来使用,所以对用的神经网络的输出应该是一个m*n的二维矩阵,其中m为batch的个数,n为分类数目,而对应的Label也是一个二维矩阵,还是拿上面的数据,组合成一个batch=2的矩阵:

所以交叉熵的结果应该是一个列向量(根据第一种方法): 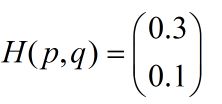
而对于一个batch,最后取平均为0.2。
在TensorFlow中实现交叉熵
在TensorFlow可以采用这种形式:
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))) - 1
其中y_表示期望的输出,y表示实际的输出(概率值),*为矩阵元素间相乘,而不是矩阵乘。
上述代码实现了第一种形式的交叉熵计算,需要说明的是,计算的过程其实和上面提到的公式有些区别,按照上面的步骤,平均交叉熵应该是先计算batch中每一个样本的交叉熵后取平均计算得到的,而利用tf.reduce_mean函数其实计算的是整个矩阵的平均值,这样做的结果会有差异,但是并不改变实际意义。
除了tf.reduce_mean函数,tf.clip_by_value函数是为了限制输出的大小,为了避免log0为负无穷的情况,将输出的值限定在(1e-10, 1.0)之间,其实1.0的限制是没有意义的,因为概率怎么会超过1呢。
由于在神经网络中,交叉熵常常与Sorfmax函数组合使用,所以TensorFlow对其进行了封装,即:
cross_entropy = tf.nn.sorfmax_cross_entropy_with_logits(y_ ,y) - 1
与第一个代码的区别在于,这里的y用神经网络最后一层的原始输出就好了。
交叉熵代价函数(损失函数)及其求导推导
置顶 2016年07月25日 00:04:44 jasonzzj 阅读数:58744 标签: logistic回归交叉熵损失函数机器学习代价函数 更多
个人分类: 机器学习
版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/jasonzzj/article/details/52017438
- 前言
- 交叉熵损失函数
- 交叉熵损失函数的求导
前言
说明:本文只讨论Logistic回归的交叉熵,对Softmax回归的交叉熵类似。
首先,我们二话不说,先放出交叉熵的公式:
J(θ)=−1m∑i=1my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))),J(θ)=−1m∑i=1my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))),
以及J(θ)对J(θ)对参数θθ的偏导数(用于诸如梯度下降法等优化算法的参数更新),如下:
∂∂θjJ(θ)=1m∑i=1m(hθ(x(i))−y(i))x(i)j∂∂θjJ(θ)=1m∑i=1m(hθ(x(i))−y(i))xj(i)
但是在大多论文或数教程中,也就是直接给出了上面两个公式,而未给出推导过程,而且这一过程并不是一两步就可以得到的,这就给初学者造成了一定的困惑,所以我特意在此详细介绍了它的推导过程,跟大家分享。因水平有限,如有错误,欢迎指正。
交叉熵损失函数
我们一共有m组已知样本,(x(i),y(i))(x(i),y(i))表示第 ii 组数据及其对应的类别标记。其中x(i)=(1,x(i)1,x(i)2,...,x(i)p)Tx(i)=(1,x1(i),x2(i),...,xp(i))T为p+1维向量(考虑偏置项),y(i)y(i)则为表示类别的一个数:
- logistic回归(是非问题)中,y(i)y(i)取0或者1;
- softmax回归(多分类问题)中,y(i)y(i)取1,2…k中的一个表示类别标号的一个数(假设共有k类)。
这里,只讨论logistic回归,输入样本数据x(i)=(1,x(i)1,x(i)2,...,x(i)p)Tx(i)=(1,x1(i),x2(i),...,xp(i))T,模型的参数为θ=(θ0,θ1,θ2,...,θp)Tθ=(θ0,θ1,θ2,...,θp)T,因此有
θTx(i):=θ0+θ1x(i)1+⋯+θpx(i)p.θTx(i):=θ0+θ1x1(i)+⋯+θpxp(i).
假设函数(hypothesis function)定义为:
hθ(x(i))=11+e−θTx(i)hθ(x(i))=11+e−θTx(i)
.
因为Logistic回归问题就是0/1的二分类问题,可以有
P(y^(i)=1|x(i);θ)=hθ(x(i))P(y^(i)=1|x(i);θ)=hθ(x(i))
P(y^(i)=0|x(i);θ)=1−hθ(x(i))P(y^(i)=0|x(i);θ)=1−hθ(x(i))
现在,我们不考虑“熵”的概念,根据下面的说明,从简单直观角度理解,就可以得到我们想要的损失函数:我们将概率取对数,其单调性不变,有
logP(y^(i)=1|x(i);θ)=loghθ(x(i))=log11+e−θTx(i),logP(y^(i)=1|x(i);θ)=loghθ(x(i))=log11+e−θTx(i),
logP(y^(i)=0|x(i);θ)=log(1−hθ(x(i)))=loge−θTx(i)1+e−θTx(i).logP(y^(i)=0|x(i);θ)=log(1−hθ(x(i)))=loge−θTx(i)1+e−θTx(i).
那么对于第ii组样本,假设函数表征正确的组合对数概率为:
I{y(i)=1}logP(y^(i)=1|x(i);θ)+I{y(i)=0}logP(y^(i)=0|x(i);θ)=y(i)logP(y^(i)=1|x(i);θ)+(1−y(i))logP(y^(i)=0|x(i);θ)=y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))I{y(i)=1}logP(y^(i)=1|x(i);θ)+I{y(i)=0}logP(y^(i)=0|x(i);θ)=y(i)logP(y^(i)=1|x(i);θ)+(1−y(i))logP(y^(i)=0|x(i);θ)=y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))
其中,I{y(i)=1}I{y(i)=1}和I{y(i)=0}I{y(i)=0}为示性函数(indicative function),简单理解为{ }内条件成立时,取1,否则取0,这里不赘言。
那么对于一共mm组样本,我们就可以得到模型对于整体训练样本的表现能力:
∑i=1my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))∑i=1my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))
由以上表征正确的概率含义可知,我们希望其值越大,模型对数据的表达能力越好。而我们在参数更新或衡量模型优劣时是需要一个能充分反映模型表现误差的损失函数(Loss function)或者代价函数(Cost function)的,而且我们希望损失函数越小越好。由这两个矛盾,那么我们不妨领代价函数为上述组合对数概率的相反数:
J(θ)=−1m∑i=1my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))J(θ)=−1m∑i=1my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))
上式即为大名鼎鼎的交叉熵损失函数。(说明:如果熟悉“信息熵“的概念E[−logpi]=−∑mi=1pilogpiE[−logpi]=−∑i=1mpilogpi,那么可以有助理解叉熵损失函数)
https://blog.csdn.net/jasonzzj/article/details/52017438这个是:交叉熵损失函数的求导
转载请注明出处:http://blog.csdn.net/jasonzzj/article/details/52017438