使用R语言进行回归诊断
人们提出所谓回归诊断的问题,其主要内容有:
- 关于误差项是否满足:独立性、等方差性、正态性。
- 选择线性模型是否合适
- 是否存在异常样本
- 回归分析的结果是否对某些样本依赖过重,也就是回归模型是否具有稳定性
- 自变量之间是否存在高度相关,即是否存在多重共线性
下面我们通过一个小例子来大体认识一下回归诊断的重要性。
一、使用散点图显示变量之间的关系及修正过程:
Anscombe<-data.frame(
X =c(10.0, 8.0, 13.0, 9.0, 11.0, 14.0, 6.0, 4.0, 12.0, 7.0, 5.0),
Y1=c(8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68),
Y2=c(9.14, 8.14, 8.74, 8.77, 9.26, 8.10, 6.13, 3.10, 9.13, 7.26, 4.74),
Y3=c(7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.44, 5.73),
X4=c(rep(8,7), 19, rep(8,3)),
Y4=c(6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.50, 5.56, 7.91, 6.89)
)
#这里y1,y2,y3是x的因变量,y4是x4的因变量,我们来查看两者之间的关系
summary(lm(Y1~X,data=Anscombe))
summary(lm(Y2~X,data=Anscombe))
summary(lm(Y3~X,data=Anscombe))
summary(lm(Y4~X4,data=Anscombe))
#通过查看变量间的线性模型概况,我们发现这四组数据模型的p值以及模型系数均能通过显著性检验
#但同时我们看到四个模型的R方值都在60%左右,不算理想
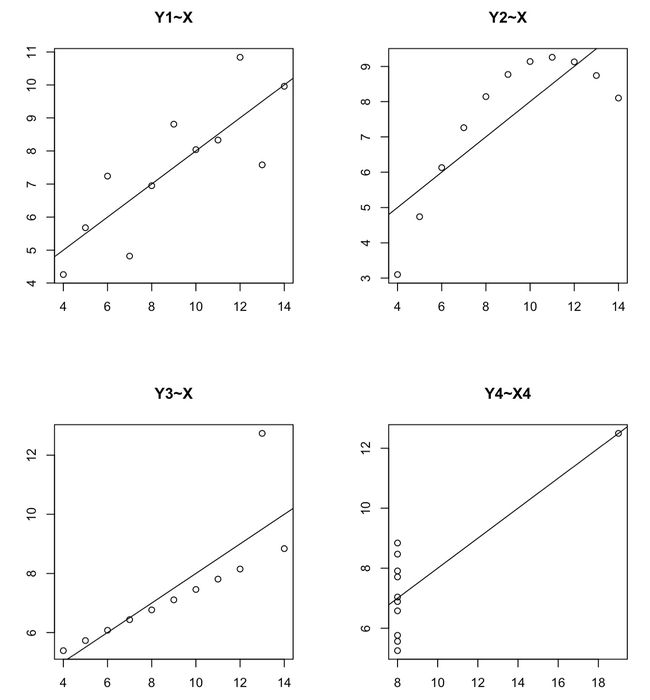
#接下来,我们通过绘制这个模型相应的散点图,以及其拟合曲线,来查看是否满足线性关系
par(mfrow=c(2,2)) #将屏幕分为2*2的矩阵
plot(Y1~X,data=Anscombe,main="Y1~X",xlab="",ylab="");abline(lm(Y1~X,data=Anscombe))
plot(Y2~X,data=Anscombe,main="Y2~X",xlab="",ylab="");abline(lm(Y2~X,data=Anscombe))
plot(Y3~X,data=Anscombe,main="Y3~X",xlab="",ylab="");abline(lm(Y3~X,data=Anscombe))
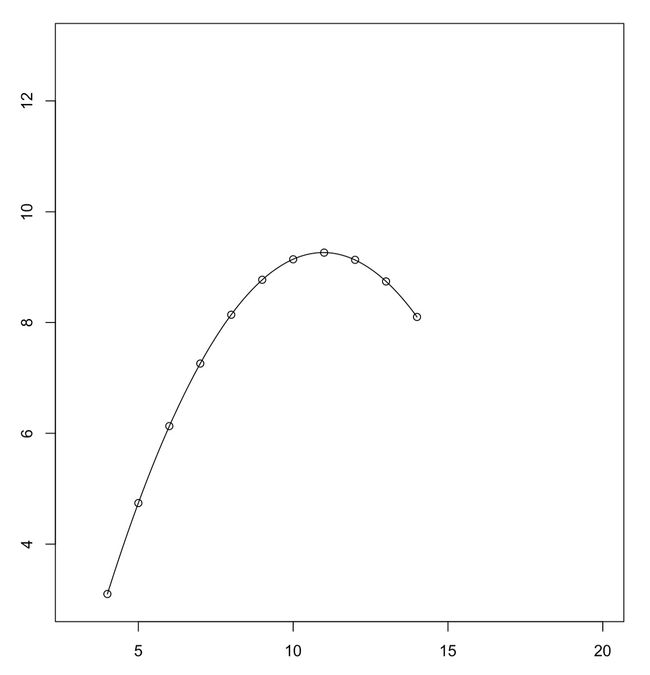
plot(Y4~X4,data=Anscombe,main="Y4~X4",xlab="",ylab="");abline(lm(Y4~X4,data=Anscombe))#我们首先对图二模型进行更新,更新为可能的二次多项式
attach(Anscombe) #表示下面的代码可以直接取Anscombe中的变量名,不必加$
X2<-X^2
lm.new<-lm(Y2~X+X2,data=Anscombe)
coef(lm.new)
x<-seq(min(X),max(X),by=0.1)
y<-b[1]+b[2]*x+b[3]*x^2
plot(c(3,20), c(3,13), type="n", xlab = "X", ylab = "Y")
points(X,Y2)
lines(x,y)
summary(lm.new)
#通过查看summary,我们看到通过二次多项式拟合之后的模型R方值为1,即完全拟合
# > summary(lm.new)
#
# Call:
# lm(formula = Y2 ~ X + X2, data = Anscombe)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.0013287 -0.0011888 -0.0006294 0.0008741 0.0023776
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -5.9957343 0.0043299 -1385 <2e-16 ***
# X 2.7808392 0.0010401 2674 <2e-16 ***
# X2 -0.1267133 0.0000571 -2219 <2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 0.001672 on 8 degrees of freedom
# Multiple R-squared: 1, Adjusted R-squared: 1
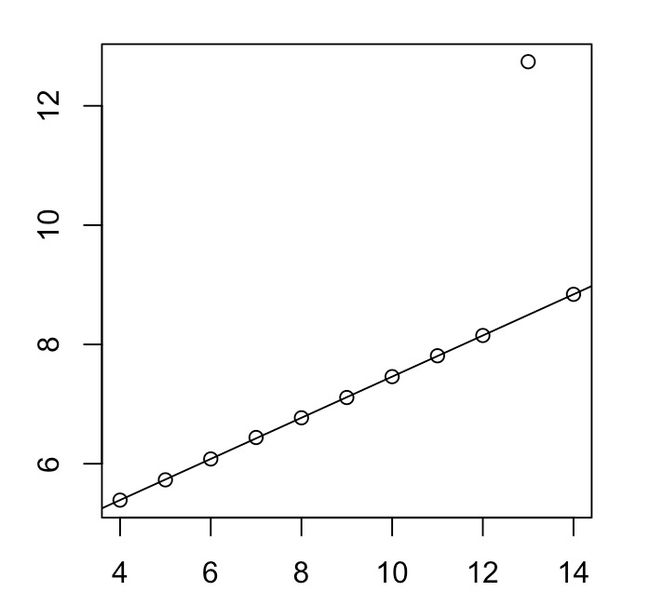
# F-statistic: 7.378e+06 on 2 and 8 DF, p-value: < 2.2e-16#对于图三和图四中因为异常点拟合有误的情况,需要去除异常点重新进行拟合,比如图三
#我们发现是第三个点(13.0.12.74)为异常点,我们将其排除
lm3.new<-lm(Y3[-3]~X[-3],data=Anscombe)
plot(X,Y3)
abline(lm3.new)
二、查看残差值:
#关于残差,我们可以通过residuals(object)来查看残差值,其中object是回归方程对象。
residuals(lm3.new)
# 1 2 3 4 5 6 7 8
# -0.0010606061 -0.0009740260 -0.0060173160 0.0038961039 -0.0012337662 -0.0008874459 -0.0008008658 -0.0011471861
# 9 10
# 0.0140692641 -0.0058441558 #通过plot(object)的方法可以查看回归模型的残差图,命令执行之后共有四个图:
#1、表示普通残差与拟合值的残差图
#2、表示画残差图的QQ图
#3、画标准化残差的开方与拟合值的残差图
#4、表示画Cook统计量的残差图什么是多重共线性,如果存在常数C1、C2、C3使得线性等式成立: C1X1+C1X2=C3
则认为变量X1和X2之间存在精确的多重共线性,但是这种情况出现基本是偶然的,如果等式换为约等式,则说明有一定程度的共线性。
在R语言中,通常用cor函数和kappa函数配合来发现变量之间的多重共线性。
最终计算的kappa值与多重共线性的关系如下:
- kappa<100则认为有共线性程度很小。
- 100<=kappa<=1000则认为存在中等程度或者较强的共线性。
- 若kappa>1000则认为存在很严重的共线性
下边举例说明其应用:
collinear<-data.frame(
Y=c(10.006, 9.737, 15.087, 8.422, 8.625, 16.289,
5.958, 9.313, 12.960, 5.541, 8.756, 10.937),
X1=rep(c(8, 0, 2, 0), c(3, 3, 3, 3)),
X2=rep(c(1, 0, 7, 0), c(3, 3, 3, 3)),
X3=rep(c(1, 9, 0), c(3, 3, 6)),
X4=rep(c(1, 0, 1, 10), c(1, 2, 6, 3)),
X5=c(0.541, 0.130, 2.116, -2.397, -0.046, 0.365,
1.996, 0.228, 1.38, -0.798, 0.257, 0.440),
X6=c(-0.099, 0.070, 0.115, 0.252, 0.017, 1.504,
-0.865, -0.055, 0.502, -0.399, 0.101, 0.432)
)
XX<-cor(collinear[2:7])
kappa(XX,exact=TRUE)
# [1] 2195.908
eigen(XX)
# > eigen(XX) 输出相关系数矩阵的特征值和特征向量
# eigen() decomposition
# $values
# [1] 2.428787365 1.546152096 0.922077664 0.793984690 0.307892134 0.001106051
#
# $vectors
# [,1] [,2] [,3] [,4] [,5] [,6]
# [1,] -0.3907189 0.33968212 0.67980398 -0.07990398 0.2510370 -0.447679719
# [2,] -0.4556030 0.05392140 -0.70012501 -0.05768633 0.3444655 -0.421140280
# [3,] 0.4826405 0.45332584 -0.16077736 -0.19102517 -0.4536372 -0.541689124
# [4,] 0.1876590 -0.73546592 0.13587323 0.27645223 -0.0152087 -0.573371872
# [5,] -0.4977330 0.09713874 -0.03185053 0.56356440 -0.6512834 -0.006052127
# [6,] 0.3519499 0.35476494 -0.04864335 0.74817535 0.4337463 -0.002166594
#通过eigen函数可以看到相关系数矩阵中的最小特征值和特征向量,取最小特征值value=0.001106051
#此时的特征向量为
# [,6]
# -0.447679719
# -0.421140280
# -0.541689124
# -0.573371872
# -0.006052127
# -0.002166594
#意味着-0.447679719x1-0.421140280x2-0.541689124x3-0.573371872x4-0.006052127x5-0.002166594x6≈0
#x5和x6系数约等于0,所以可以基本认为-0.447679719x1-0.421140280x2-0.541689124x3-0.573371872x4≈0