简单神经网络在Numpy和Pytorch上的实现
我们将实现一个只有输入层、单隐藏层、输出层的一个神经网络。假设样本数为64个,输入维度为1000,隐藏层为100,输出层为10。
神经网络的求导,本质上是求导的链式法则。但由于涉及矩阵的乘法,有时候就会使用到转置,从而保证矩阵相乘的正确。那什么时候需要添加转置操作呢?能想到的办法就是根据结果去反推或者采用矩阵的求导法则,具体可参考(https://blog.csdn.net/herosunly/article/details/89005067),具体可见如下代码:
Numpy代码
num_samples = 64 # N
dim_in, dim_hid, dim_out = 1000, 100, 10 # IN H OUT
x = np.random.randn(num_samples, dim_in) # N * IN
y = np.random.randn(num_samples, dim_out) # N * OUT
w1 = np.random.randn(dim_in, dim_hid) # IN * H
w2 = np.random.randn(dim_hid, dim_out) # H * OUT
eta = 1e-6
for i in range(1000):
#Forward pass
h = x @ w1 # N * H
h_relu = np.maximum(h, 0) # N * H
y_pred = h_relu @ w2 # N * OUT
#Loss
loss = np.square(y_pred - y).sum()
print('times is {}, loss is {}'.format(i, loss))
#Backward pass
grad_y_pred = 2.0 * (y_pred - y) # N * OUT
grad_w2 = (h_relu.T) @ (grad_y_pred) #H * OUT = (H * N) * (N * OUT),其中(H * N) = (N * H).T
grad_h_relu = grad_y_pred @ ((w2.T))# N * H = (N * OUT) * (OUT * H),其中(OUT * H) = (H * OUT).T
grad_h = grad_h_relu.copy()
grad_h[h < 0] = 0
grad_w1 = (x.T) @ (grad_h) # IN * H = (IN * N) * (N * H)
w1 = w1 - eta * grad_w1
w2 = w2 - eta * grad_w2
其中@表示矩阵的乘法。
Pytorch代码
num_samples = 64 # N
dim_in, dim_hid, dim_out = 1000, 100, 10 # IN H OUT
x = torch.randn(num_samples, dim_in) # N * IN
y = torch.randn(num_samples, dim_out) # N * OUT
w1 = torch.randn(dim_in, dim_hid) # IN * H
w2 = torch.randn(dim_hid, dim_out) # H * OUT
eta = 1e-6
for i in range(1000):
#Forward pass
h = x @ w1 # N * H
h_relu = h.clamp(min = 0) # N * H
y_pred = h_relu @ w2 # N * OUT
#Loss
loss = (y_pred - y).pow(2).sum().item()
print('times is {}, loss is {}'.format(i, loss))
#Backward pass
grad_y_pred = 2.0 * (y_pred - y) # N * OUT
grad_w2 = (h_relu.t()) @ (grad_y_pred) #H * OUT = (H * N) * (N * OUT),其中(H * N) = (N * H).T
grad_h_relu = grad_y_pred @ ((w2.t()))# N * H = (N * OUT) * (OUT * H),其中(OUT * H) = (H * OUT).T
grad_h = grad_h_relu.clone()
grad_h[h < 0] = 0
grad_w1 = (x.t()) @ (grad_h) # IN * H = (IN * N) * (N * H)
w1 = w1 - eta * grad_w1
w2 = w2 - eta * grad_w2
Pytorch优化代码一
num_samples = 64 # N
dim_in, dim_hid, dim_out = 1000, 100, 10 # IN H OUT
x = torch.randn(num_samples, dim_in) # N * IN
y = torch.randn(num_samples, dim_out) # N * OUT
w1 = torch.randn(dim_in, dim_hid, requires_grad=True) # IN * H
w2 = torch.randn(dim_hid, dim_out, requires_grad=True) # H * OUT
eta = 1e-6
for i in range(1000):
#Forward pass
h = x @ w1 # N * H
h_relu = h.clamp(min = 0) # N * H
y_pred = h_relu @ w2 # N * OUT
#Loss
loss = (y_pred - y).pow(2).sum()
print('times is {}, loss is {}'.format(i, loss.item()))
loss.backward()
#Backward pass
with torch.no_grad():
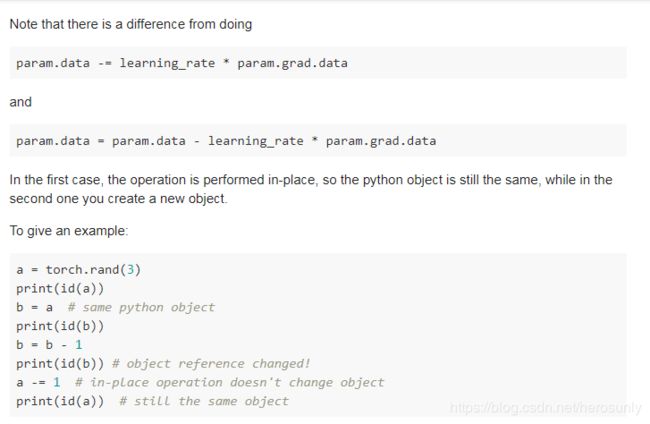
w1 -= eta * w1.grad #如果写成w1 = w1 - eta * w1.grad就会报错,报错原因不明
w2 -= eta * w2.grad
w1.grad.zero_()
w2.grad.zero_()
https://discuss.pytorch.org/t/what-is-the-recommended-way-to-re-assign-update-values-in-a-variable-or-tensor/6125/2
使用Pytorch nn
import torch
num_samples = 64 # N
dim_in, dim_hid, dim_out = 1000, 100, 10 # IN H OUT
x = torch.randn(num_samples, dim_in) # N * IN
y = torch.randn(num_samples, dim_out) # N * OUT
# 提前定义模型
model = torch.nn.Sequential(
torch.nn.Linear(dim_in, dim_hid, bias = False), #model[0]
torch.nn.ReLU(),
torch.nn.Linear(dim_hid, dim_out, bias = False),#model[2]
)
torch.nn.init.normal_(model[0].weight) # 如果不加这两行代码,loss下降的会很慢
torch.nn.init.normal_(model[2].weight)
#提前定义loss函数
loss_fun = torch.nn.MSELoss(reduction='sum')
eta = 1e-6
for i in range(1000):
#Forward pass
y_pred = model(x)
#Loss
loss = loss_fun(y_pred, y)
print(i, loss.item())
loss.backward()
#Backward pass
with torch.no_grad():
for param in model.parameters(): # param (tensor, grad)
param -= eta * param.grad
model.zero_grad()
PyTorch: optim
num_samples = 64 # N
dim_in, dim_hid, dim_out = 1000, 100, 10 # IN H OUT
x = torch.randn(num_samples, dim_in) # N * IN
y = torch.randn(num_samples, dim_out) # N * OUT
# 提前定义模型
model = torch.nn.Sequential(
torch.nn.Linear(dim_in, dim_hid, bias = False), #model[0]
torch.nn.ReLU(),
torch.nn.Linear(dim_hid, dim_out, bias = False),#model[2]
)
torch.nn.init.normal_(model[0].weight)
torch.nn.init.normal_(model[2].weight)
#提前定义loss函数和优化函数
loss_fun = torch.nn.MSELoss(reduction='sum')
eta = 1e-6
optimizer = torch.optim.SGD(model.parameters(), lr=eta)
for i in range(1000):
#Forward pass
y_pred = model(x)
#Loss
loss = loss_fun(y_pred, y)
print(it, loss.item())
optimizer.zero_grad()
# Backward pass
loss.backward()
# update model parameters
optimizer.step()
Adam
num_samples = 64 # N
dim_in, dim_hid, dim_out = 1000, 100, 10 # IN H OUT
x = torch.randn(num_samples, dim_in) # N * IN
y = torch.randn(num_samples, dim_out) # N * OUT
# 提前定义模型
model = torch.nn.Sequential(
torch.nn.Linear(dim_in, dim_hid, bias = False), #model[0]
torch.nn.ReLU(),
torch.nn.Linear(dim_hid, dim_out, bias = False),#model[2]
)
# torch.nn.init.normal_(model[0].weight) #修改一
# torch.nn.init.normal_(model[2].weight)
#提前定义loss函数和优化函数
loss_fun = torch.nn.MSELoss(reduction='sum')
eta = 1e-4 #修改二
optimizer = torch.optim.Adam(model.parameters(), lr=eta)
for i in range(1000):
#Forward pass
y_pred = model(x)
#Loss
loss = loss_fun(y_pred, y)
print(it, loss.item())
optimizer.zero_grad()
# Backward pass
loss.backward()
# update model parameters
optimizer.step()
PyTorch: 自定义 nn Modules
num_samples = 64 # N
dim_in, dim_hid, dim_out = 1000, 100, 10 # IN H OUT
x = torch.randn(num_samples, dim_in) # N * IN
y = torch.randn(num_samples, dim_out) # N * OUT
class TwoLayerNet(torch.nn.Module):
def __init__(self, dim_in, dim_hid, dim_out):
super(TwoLayerNet, self).__init__()
# define the model architecture
self.linear1 = torch.nn.Linear(dim_in, dim_hid, bias=False)
self.linear2 = torch.nn.Linear(dim_hid, dim_out, bias=False)
def forward(self, x):
y_pred = self.linear2(self.linear1(x).clamp(min=0))
return y_pred
# 提前定义模型
model = TwoLayerNet(dim_in, dim_hid, dim_out)
#提前定义loss函数
loss_fun = torch.nn.MSELoss(reduction='sum')
eta = 1e-4
optimizer = torch.optim.Adam(model.parameters(), lr=eta)
for i in range(1000):
#Forward pass
y_pred = model(x)
#Loss
loss = loss_fun(y_pred, y)
print(i, loss.item())
optimizer.zero_grad()
# Backward pass
loss.backward()
# update model parameters
optimizer.step()