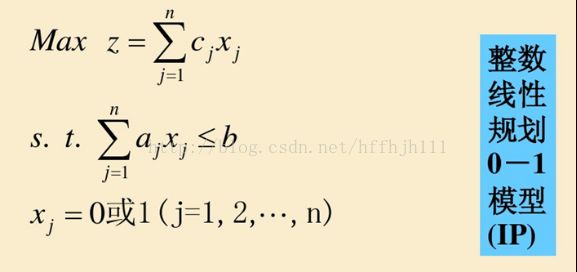算法篇-5-动态规划-01背包&流水作业调度&&整数线性规划&树的最大连通分支

本系列所有代码https://github.com/YIWANFENG/Algorithm-github

0-1背包

给定N中物品和一个背包。物品i的重量是Wi,其价值位Vi ，背包的容量为C。问应该如何选择装入背包的物品，使得转入背包的物品的总价值为最大？

且对于物品i只有装一次或者一次不装两种选择。

 

令m(i,j)表示后i到n (1<=i<=n)个物品中能够装入容量为j(1<=j<=C)的背包中的物品的最大价值，则可以得到如下的动态规划函数:

m(n,j) = vn j>=wn;

(2) m(n,j) = 0   0<=j

(3)  m(i,j)=m(i+1,j)  0<=j

 (4)  m(i,j)=max{m(i+1,j) ,m(i+1,j-wi)+vi)} j>wi

(3) 式表明：如果第i个物品的重量大于背包的容量，则装入i物品得到的最大价值和装入i+1物品得到的最大价是相同的，即物品i不能装入背包；第(4)个式子表明:如果第i个物品的重量小于背包的容量，则会有一下两种情况：(a)如果把第i个物品装入背包，则背包物品的价值等于第i+1个物品装入容量位j-wi 的背包中的价值加上第i个物品的价值vi; (b)如果第i个物品没有装入背包，则背包中物品价值就等于把i+1后物品装入容量为j的背包中所取得的价值。显然，取二者中价值最大的作为把后i个物品装入容量为j的背包中的最优解。

(1)(2) 确定了边界。

以上是为了配合代码从后向前分析，其实我们完全可以从前向后分析，

那么:

m(1,j) = 0;   0<=j

m(1,j) = v1;   j>wi;

m(i,j) = m(i-1,j);    0<=j

m(I,j) = max{ m(i-1,j) , m(i-1,j-wi)+vi};   j>wi;

 

 

Code:

template
void Knapsack(T_ v[],intw[],int c,int n,T_ m[])
{
       //v[]/w[] 每物品价值 /重量
       //c背包容量，n物品个数，m最优值结果
       //m[i][j] 表示背包容量为j ,可选物品为 {i,i+1,...,n}时的最优解
       int jMax = w[n]-1>c?c:w[n]-1;
       for(int j=0; j<=jMax; j++) m[n*(c+1)+j]=0;
       for(int j=w[n]; j<=c; j++) m[n*(c+1)+j] = v[n];
       for(int i=n-1; i>1; i--) {
              //计算第i物品，放入背包时的最优值。
              jMax =w[i]-1>c?c:w[i]-1;
              for(int j=0;j<=jMax; j++)
                     m[i*(c+1)+j] = m[(i+1)*(c+1)+j];
             
              for(int j=w[i];j<=c; j++) {
                     T_ bb = (m[(i+1)*(c+1)+(j-w[i])]+v[i]);
                     m[i*(c+1)+j] = m[(i+1)*(c+1)+j]>bb?m[(i+1)*(c+1)+j]:bb;
              }
              //只计算i=1时最后一个，节省一点计算
              m[c+1+c]=m[2*(c+1)+c];
              if(c>=w[1]) {
                     T_ cc = m[2*(c+1)+(c-w[1])]+v[1];
                     m[c+1+c] = m[c+1+c]>cc?m[c+1+c]:cc;
              }
       } 
}
 
template
void Traceback(T_m[],int w[],int c,int n,int x[])
{
       //m[i][j] 表示背包容量为j ,可选物品为 {i,i+1,...,n}时的最优解
       //w[] 每物品价值 /重量
       //c背包容量，n物品个数
       //x[]选择结果序列
       int current_c=c;
       for(int i=1; i

 

 流水作业调度

n个作业{1，2，…，n}要在由2台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工，然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi。流水作业调度问题要求确定这n个作业的最优加工顺序，使得从第一个作业在机器M1上开始加工，到最后一个作业在机器M2上加工完成所需的时间最少。

整数线性规划

设m(i,j) 为选择前I 项，总资源为j时的最优回报值。

Wi为投资i单位所需资源

Vi 为投资I 后单位所获回报

Xi 为投资I 多少单位

 

那么类似01背包可得

M(1,j) = 0 , j

M(1,j)=k* v1 ,k*w1 <=j<(k+1)w1;

M(i,j) = m(i-1,j) , j

M(i,j) = max{ m(i-1,j) ,max{m(i-1,j-x*wi)+x*vi}(1<=x<=k)} , k*wi<=j<(k+1)wi;

 

Code:

 

void how_to_invest(intn,int all,int w[],int v[])
{
       //n个选项  all=所有资源
       //x[i]/w[i]/v[i] 第i个项目投资了多少单位/单位需求资源数/单位回报数
       //m[i][j]为选择前i项，总资源为j时的最优回报值。 
       //X[i][j]该最由下投资第i物品多少单位
       for(int i=1; i<=n; i++) m[i][0]=0;
       for(int i=1; i=w[i];
                     //max{m(i-1,j-x*wi)+x*vi}(1<=x<=k)}
                     int Mmax = 0;
                     int k = int(j/w[i]);
                     for(int x=w[i]; x<=k; x++) {
                            if(MmaxMmax) {
                            m[i][j]=m[i-1][j];
                            X[i][j]=0;
                     } else {
                            m[i][j]= Mmax;
                     }
              }
       }
}
 
 
void TraceBack(intw[],int n,int all) {
       //n个选项  all=所有资源
       if(X[n][all]==-1) return ;
       if(X[n][all]!=0) {
              cout<<"第"<

 

树的最大连通分支

给定一棵树，树中每个顶点u都有一个权w(u)，权可以为负数，现找出树T的一个联通子图使该子图权之和最大。

 

先用孩子兄弟节点构造一棵树，从该树的叶子节点开始，若该结点的子树权重为正，则加他到该节点权重上，否则不加，若没子树，则该节点的权重即为原权重。遍历方式是自底向上，层级优先。

设S(i)是以i为顶层节点的联通子图对应的最优值，S(i) = w(i) + sum(S(k)) S(k)>0,S(k)为i为根的树的子树。最终结果即为Max(S(i))。