【分治算法】归并排序,快速排序和汉诺塔
1介绍
分治算法已经是本人所写的常用算法系列的第三个了,可能只会写这一节,对比动态规划与贪心算法我们来认识一下分治算法。从思路上来看:
(1)动态规划:多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解。每一个阶段的最优解是基于前一个阶段的最优解。
(2)贪心算法:选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。不是对所有问题都能得到整体最优解。
(3)分治算法:将一个大规模的问题分解成n个容易解决的小问题,当小问题被解决时,最终的问题也被解决了。
乍一看,似乎区别不大。
从代码结构上来看(不绝对):
(1) 动态规划:通常为两层for循环嵌套;
(2) 贪心算法:通常先进行排序,后进行选择;
(3) 分治算法:通常为递归;
2归并排序
2.1问题
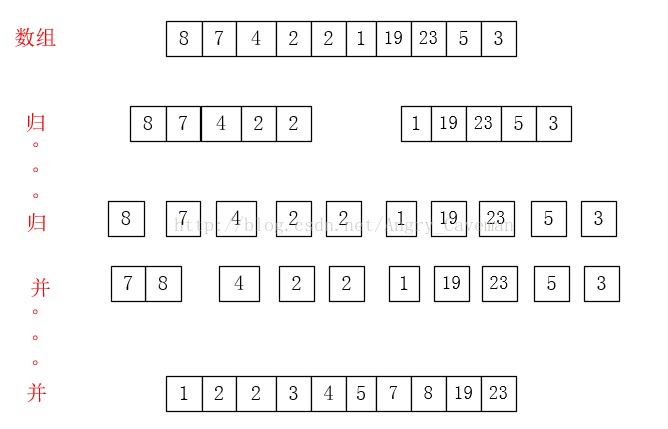
问题:使用归并排序以下数字:8,7,4,2,2,1,19,23,5,3
2.2解析
按照分治算法的思想,题中数组Array有10个数字,不太方便操作,应该将其分解为若干个容易解决的子问题。假设现在排序的是包含1个数字的数组Array,是不是就非常容易了(一个数字都不用排序)。现将数组Array分解为10个数组,每个数组只含有1个数字,这就是归并排序中“归”的过程。
数组只含有1个数字,可见该数组已经有序了。然后将两个有序的数组合并起来,当然合并的时候也要确保合并之后的数组也是有序的。这就是归并排序中“并”的过程。
归并排序的处理过程:
(1)“归”:拆分为只含有一个数字的数组;
void SplitSort(int first,int last,int a[],int temp[]){
if (last>first){
int mid = (first + last) / 2;
SplitSort(first,mid,a,temp);
SplitSort(mid+1,last,a,temp);
MergeSort(first,last,mid,a,temp);
}
}
(2)“并”:将两个有序的数组合并成一个有序的数组;
void MergeSort(int first,int last,int mid,int a[],int temp[]){
int i = first, j = mid + 1;
int m = mid, n = last;
int k = 0;
while (i <= m && j <= n)
{
if (a[i] <= a[j])
temp[k++] = a[i++];
else
temp[k++] = a[j++];
}
while (i <= m)
temp[k++] = a[i++];
while (j <= n)
temp[k++] = a[j++];
for (i = 0; i < k; i++)
a[first + i] = temp[i];
}
本题完整源代码:
#include
using namespace std;
#define Max 10
//归并排序
void MergeSort(int first,int last,int mid,int a[],int temp[]){
int i = first, j = mid + 1;
int m = mid, n = last;
int k = 0;
while (i <= m && j <= n)
{
if (a[i] <= a[j])
temp[k++] = a[i++];
else
temp[k++] = a[j++];
}
while (i <= m)
temp[k++] = a[i++];
while (j <= n)
temp[k++] = a[j++];
for (i = 0; i < k; i++)
a[first + i] = temp[i];
}
void SplitSort(int first,int last,int a[],int temp[]){
if (last>first){
int mid = (first + last) / 2;
SplitSort(first,mid,a,temp);
SplitSort(mid+1,last,a,temp);
MergeSort(first,last,mid,a,temp);
}
}
bool Merge(int a[],int n){
int *temp = new int[n];
if (temp == NULL)
return false;
SplitSort(0,n-1,a,temp);
return true;
}
int main(){
int array[Max] = { 8, 7, 4, 2, 2, 1, 19, 23, 5, 3 };
Merge(array,Max);
//打印
int i;
for (i = 0; i < Max;i++){
cout << array[i] << " ";
}
return 0;
} 2.3结果
3快速排序
3.1问题
问题:使用快速排序一下数字:8,7,4,2,2,1,19,23,5,3
3.2解析
同样按照分治算法思想,还是要将其拆分为容易解决的子问题,不过,与归并算法的不同之处在于不是将其拆分为只含一个数字的数组,毕竟容易解决地子问题不只那一个。
抛开眼前的问题,假设现在有一个数组Array[3]={3,1,2},如果我们要对其排序的话,可以得到Array[1]==1,可见,只有让在数组中大于Array[1]的数字位于其右边(Array[1]), 小于Array[1]的数字位于其左边(Array[0]),那么Array也就有序了。
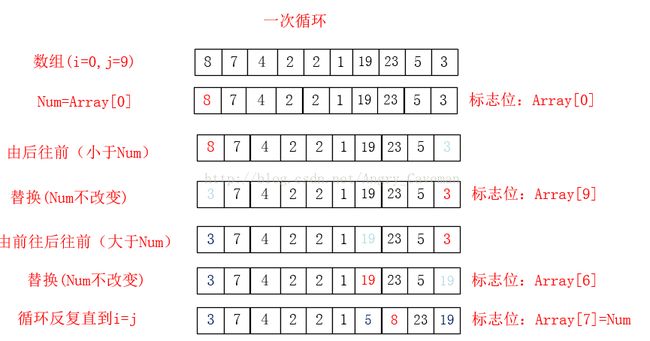
基于以上推导,这个容易解决的子问题就是,让大于某个数的数字位于其右边,小于该数字则位于其左边,这个数在快速排序中称为基数。当然还有很多困惑的地方,比如,基数左右两边的数组仍然是乱序的,结合下图来看看详细的快速排序过程。
快速排序:
(1) 从数组Array[n]中任意选取一个数作为基数num,默认num=Array[0];并将此处设为标志位。
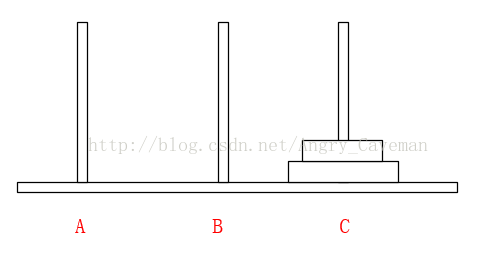
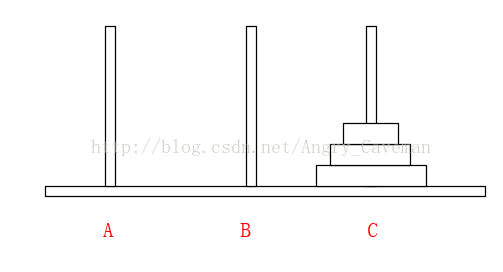
(2) 在Array[n]中,从后往前找小于num的数字,若Array[m1] (3) 随后,由之前的标志位往(0)后找,若Array[m2]>num, 则将此数字放置在标志位m1上,并将m2设为标志位。 (4) 如图直到i=j,一次循环结束。此时左右的两边的数组仍然是乱序的,我们把左右两边的数组分别看成独立的数组,让其也进行同样的循环,最终得到结果。 本题完整源代码: 汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问应该如何操作? 首先要说明的一点是,以目前个人电脑的运行速度,基本上得不到64片黄金盘的结果。所以此处使用n片,n为随意输入的数字。 另外,题目有两个条件:(1)小圆盘上都不能放大圆盘;(2)一次只能移动一片。 如果只有2片,由A柱移动到C柱需要进行三次操作 如果有3片的话,我们再来看看。 一共需要7步,总结过程: (1) 前3步一样,最顶层2个由A柱移动到了B柱; (2) 最大的盘由A柱移动到C柱; (3) 又是3步一样的移动,最顶层2个由B柱移动到了C柱; 由此可以推导出,F(n)=2F(n-1)+1。由该式可以看出应该使用递归。也就是说要得到n片怎么挪动,就应先知道n-1片怎么挪动,以此类推直到知道2片怎么挪动。 可以直接这样理解: 不是说一次只能移动一片吗?因为除了最底层的盘,其上的n-1盘的移动都已经知道(递归),省略了具体步骤而已。 源代码: 算法之前就打算只写这三类(动态规划,贪心算法,分治算法),感觉用的也比较多,整个过程自己也学到不少东西,希望能共勉吧。#include3.3结果
![]()
4汉诺塔
4.1问题
4.2解析
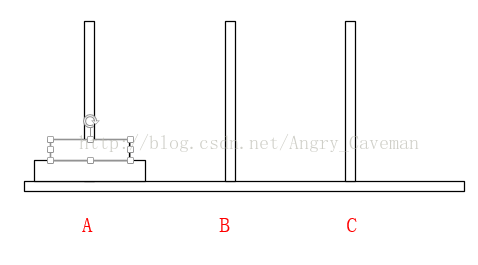
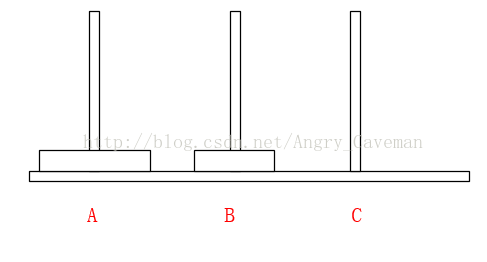
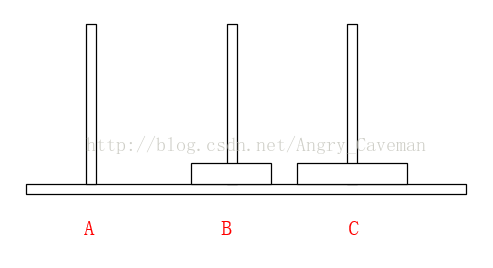
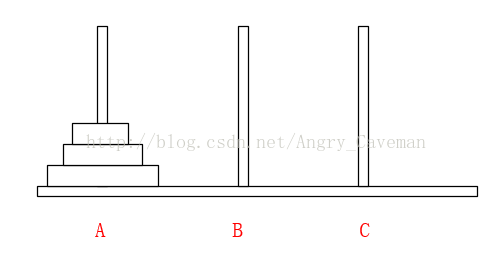
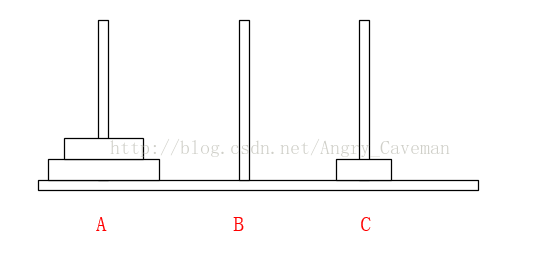
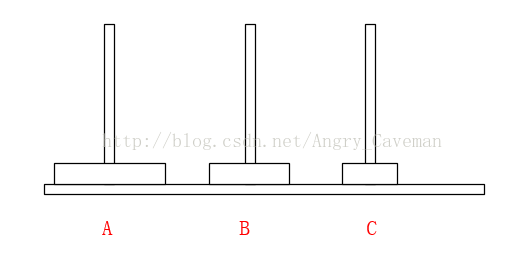
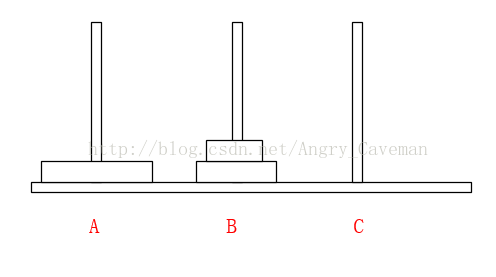
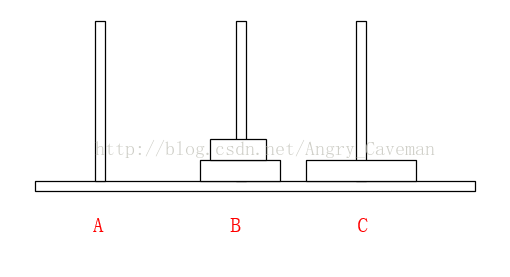
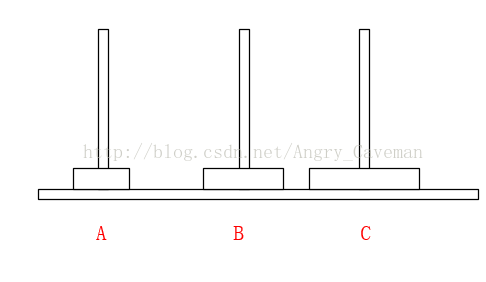
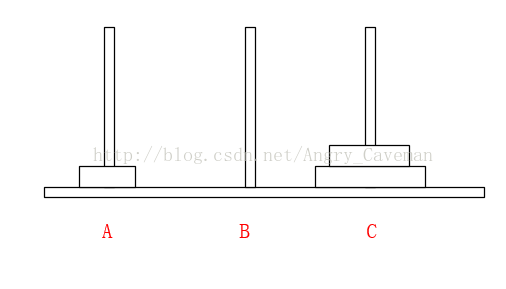
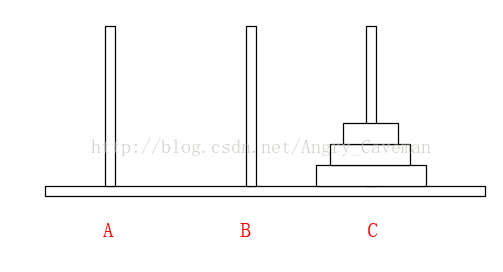
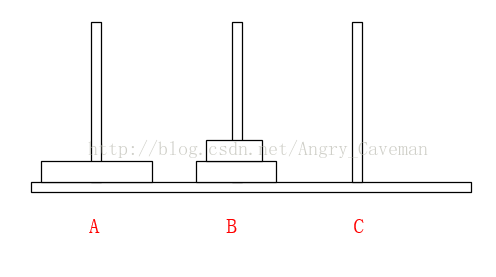
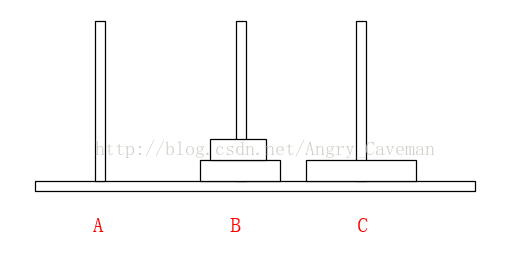
#include4.3结果

5总结