LOJ 6437 PKUSC2018 PKUSC

Problem

LOJ
……在最后附赠一个数据生成器吧

Solution

我调试调了一天……把网上唯二的一篇题解扒下来拍，然后就开始各种nan。改了好久结果跑出来一组hack题解的数据。。然后又扒了boshi的，又把boshi的代码给hack了几次……然而一直都只有70pts，答案相差不多。。
最后扒了loj上rank1的同样方法的大佬的代码，输出了中间结果，才发现我eps设小了，eps一直设到1e-3才A。哭晕在厕所qwqq

讲一讲思路吧，每个点的权值都是1，那么期望就是所有点落在多边形内的和。不如把点分开进行考虑，对于点P落入多边形的概率就是以原点为圆心，旋转P所产生的圆与多边形交集的弧度和与360度的比值。这个东西怎么求呢，不妨从原点对多边形进行三角剖分，然后类似于求多边形面积，我们同样可以根据顺逆时针来累加答案，不过其实最后输出答案还是建议加fabs，要避免-0.00000这种东西。

当然了，你需要玄学调参分类讨论。在以下讨论之前，我们先假定逆时针旋转为加，顺时针为减。

比如说这样的情况，它的答案应该是0.04324。

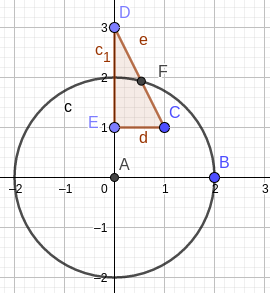
对于CE这条边它是没有贡献的，因为这条边完全在圆内。而对于CD这条边，有贡献的应该是DF区间，所以我们应该算DF所对的圆心角，怎么算呢？为了减小误差，我用了正弦定理。首先根据余弦定理可以算∠C的度数，再利用EF=r，我们可以用余弦定理算出∠CFE的度数，那么∠CEF的度数就可以得到了，然后再用∠COD的去减。

然而还有这种情况，它的答案应该是0.28205。

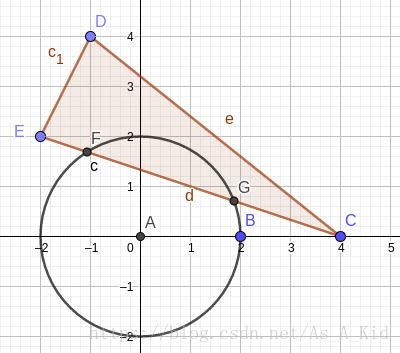
CD，DE都有贡献，但CE边贡献不同。贡献是∠FAG，在当前讨论的情况下看应该是减去∠CAG和∠EAF。这个就比较方便了，用点到直线距离公式求出距离dist，然后用垂径定理我们可以知道中间夹角是2*acos(d/r)。

注意原点是不会旋转的，所以原点要特判是否在多边形内，由于是严格，在边上也不能算。
注意如果有一条边所在直线是过圆点的，请直接判掉continue。不然如果对于某条边如果刚好过原点，且是第一种特殊情况时(即两个端点一个在圆内一个在圆外)，在算alpha角的时候可能会因为精度误差导致传入的cos比-1小了个eps，然后算出来的alpha角就变成了nan，就炸了……
还有为什么eps要开大点？因为数据中出的某些点在圆的边上，而且因为精度误差有点大，为了避免少计算到某些蹭在圆外的边，你需要+eps来判定。

时间复杂度是$O(nm)$的。

Code

#include 
#include 
#include 
#define rg register
using namespace std;
typedef long long ll;
const int maxn=510;
const double pi=acos(-1.0),eps=1e-3;
template <typename Tp> inline void getmin(Tp &x,Tp y){if(y<x) x=y;}
template <typename Tp> inline void getmax(Tp &x,Tp y){if(y>x) x=y;}
template <typename Tp> inline void read(Tp &x)
{
	x=0;int f=0;char ch=getchar();
	while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
	if(ch=='-') f=1,ch=getchar();
	while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
	if(f) x=-x;
}
struct vec{
	double x,y;
	vec(){}
	vec(double _x,double _y){x=_x;y=_y;}
	vec operator + (const vec &t)const{return vec(x+t.x,y+t.y);}
	vec operator - (const vec &t)const{return vec(x-t.x,y-t.y);}
	double operator * (const vec &t)const{return x*t.x+y*t.y;}
	double operator / (const vec &t)const{return x*t.y-y*t.x;}
	vec rev(){return vec(y,-x);}
}o,cz,a[maxn],p[maxn];
struct line{
	double a,b,c;
	line(){}
	line(double _a,double _b,double _c){a=_a;b=_b;c=_c;}
	double dis(vec t){return fabs(a*t.x+b*t.y+c)/sqrt(a*a+b*b);}
}l;
int n,m,f;
double q,d,d1,d2,dist,alpha,beta,rd,ans;
inline double fabs(double x){return x<0?-x:x;}
line transform(vec a,vec b)
{
	if(fabs(a.x-b.x)<=eps){return line(1,0,-a.x);}
	double k=(b.y-a.y)/(b.x-a.x),b0;
	b0=a.y-a.x*k;
	return line(k,-1,b0);
}
int inpoly(vec t)
{
	double k,d1,d2;int wn=0;
	for(rg int i=1;i<=m;i++)
	{
		if((a[i]-t)/(a[i-1]-t)==0&&(a[i]-t)*(a[i-1]-t)<=0) return 2;
		k=(t-a[i-1])/(a[i]-a[i-1]);
		d1=a[i-1].y-t.y;d2=a[i].y-t.y;
		if(k>0&&d1<=0&&d2>0) wn++;
		if(k<0&&d2<=0&&d1>0) wn--;
	}
	return wn!=0;
}
int main()
{
	#ifndef ONLINE_JUDGE
	freopen("in.txt","r",stdin);
	#endif
	read(n);read(m);
	for(rg int i=1;i<=n;i++) read(p[i].x),read(p[i].y);
	for(rg int i=1;i<=m;i++) read(a[i].x),read(a[i].y);
	a[0]=a[m];o.x=o.y=0.0;
	for(rg int i=1;i<=m;i++)
	  for(rg int j=1;j<=n;j++)
	  {
	  	d1=a[i]*a[i];d2=a[i-1]*a[i-1];
	  	q=(a[i]-a[i-1])*(a[i]-a[i-1]);
	  	if(d1<=eps||d2<=eps||fabs(q)<=eps||fabs(a[i-1]/a[i])<=eps) break;
	    if(d1>d2) swap(d1,d2);
	    l=transform(a[i-1],a[i]);
		dist=l.dis(o);cz=(a[i]-a[i-1]).rev();//cz是垂直向量
	    if(fabs(p[j].x)>eps||fabs(p[j].y)>eps)
		{
		  	d=p[j]*p[j];
		  	rd=acos((d1+d2-q)/2/sqrt(d1)/sqrt(d2));
		  	if((d1-d)*(d2-d)<0)
		  	{
		  		alpha=acos((d1+q-d2)/2/sqrt(d1)/sqrt(q));
		  		beta=asin(sin(alpha)*sqrt(d1/d));
		  		rd-=pi-alpha-beta;
		  	}
			else if((d1+eps>d)&&(d2+eps>d))
			{
				if((cz/a[i-1])*(cz/a[i])<0&&dist<sqrt(d))
				  rd-=2.0*acos(dist/sqrt(d));
		  	}
		  	else rd=0.0;
		  	if(a[i-1]/a[i]>0) ans+=rd/2.0/pi;
		  	else ans-=rd/2.0/pi;
		}
	  }
	ans=fabs(ans);f=inpoly(o);
	for(rg int i=1;i<=n&&f==1;i++)
	  if(fabs(p[i].x)<=eps&&fabs(p[i].y)<=eps)
	    ans+=1.0;
	printf("%.5lf\n",ans);
	return 0;
}

---

数据生成器

#include 
using namespace std;
#define rg register
#define oo (0x3f3f3f3f)
#define eps (1e-10)

struct point{double x,y;};
point sta[210],dot[210];
int top=0,n=200,m=2,li=1000000;

inline double dis(point aa,point bb){return sqrt((aa.x-bb.x)*(aa.x-bb.x)+(aa.y-bb.y)*(aa.y-bb.y));}

inline double mul(point p1,point p2,point p3){
    p2.x-=p1.x,p2.y-=p1.y,
    p3.x-=p1.x,p3.y-=p1.y;
    return p2.x*p3.y-p2.y*p3.x;
}

inline int comp(const point p1,const point p2){
    double tmp=mul(dot[0],p1,p2);
    if(fabs(tmp-0.0)<eps)
        if(dis(dot[0],p1)<dis(dot[0],p2))return 1;
        else return 0;
    else
        return tmp>0;
}

inline int rd(){return (rand()&1?1:-1)*(rand()%li);}

void tubao(){
    sta[0]=dot[0],sta[1]=dot[1],sta[2]=dot[2],top=2;
    for(rg int i=3;i<=n;++i){
//      while(mul(sta[top-1],sta[top],dot[i])<=0)--top;
        sta[++top]=dot[i];
    }
    for(rg int i=1;i<=top;++i)printf("\n%.0lf %.0lf",sta[i].x,sta[i].y);
    return ;
}

int main(){
    freopen("in.txt","w",stdout);
    srand(time(0));
    double tmpx,tmpy;int tmp;
    printf("%d %d\n\n0 0\n",m,n);
    for(int i=2;i<=m;i++)
      printf("%d %d\n",rd(),rd());
    tmpy=+oo;
    for(rg int i=0;i<n;++i)dot[i].x=rd(),dot[i].y=rd();
      for(rg int i=0;i<n;++i)
        if(dot[i].y<tmpy||(dot[i].y==tmpy&&dot[i].x<tmpx))
          {tmpx=dot[i].x,tmpy=dot[i].y,tmp=i;}
    swap(dot[0],dot[tmp]);
    sort(dot+1,dot+n,comp);
    dot[n]=dot[0];
    tubao();
    return 0;
}