算法分析与设计（二）

动态规划

• 编辑距离（Levenshtein距离）

比较两个字符串时，若字符串$x$长度为m，字符串$y$长度为n。
假设这两个字符串之间的编辑距离为$E(m,n)$。
要通过动态规划的方式解决它，那就需要将这样一个问题划分为子问题$E(i,j)$，子问题表示串$x$中前$i$个字符与串$y$中前$j$个字符之间的编辑距离。
当计算子串的编辑距离时，子串的最右边一列对齐时有以下三种情形：

$$\begin{gathered} \_x[i]x[i] \\ y[j]\_y[j] \end{gathered}$$

根据以上的对齐方式，可以得到$E(i,j)$的递推公式：

$$\begin{gathered} E(i,j)=min\{1+E(i-1,j),1+E(i,j-1),diff(i,j)+E(i-1,j-1)\}; \\ Ifx[i]==y[i]thendiff(i,j)=0,otherwisediff(i,j)=1; \\ E(0,j)=j;E(i,0)=i \end{gathered}$$

根据以上递推公式，便能计算并填写下列表格，最终的$E(m,n)$即为最小编辑距离

$E(i,j)$		x[1]	x[2]	…	x[i]	…	x[m]
	0	1	2	…	i	…	m
y[1]	1
y[2]	2
…	…
y[j]	j
…	…
y[n]	n

计算编辑距离的时间复杂度为
$$O(m\cdot n)$$

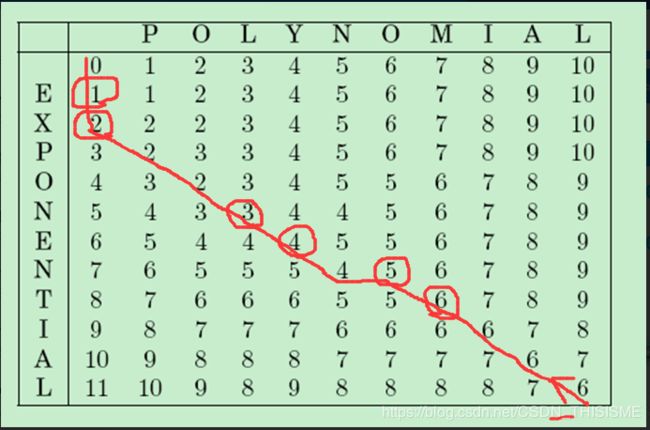
计算出编辑距离后，要想求出字符串的编辑位置，则可以从$E(m,n)$开始与左边、上边或左上角移动一格的区域中找出最小的一个编辑距离即$E{d}_{min}=min\{E(m-1,n),E(m,n-1),E(m-1,n-1)\}$，将其与$E(m,n)$比较，若两者相等则说明$x[m]$与$y[n]$是对齐且相等的；否则认为这一位置是编辑点。同时继续以$E{d}_{min}$对应的位置开始继续以上的步骤。

如下图说示，为两字符串的编辑位置。

• 邮差问题

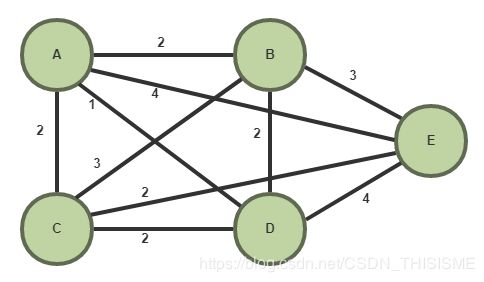
给定一个加权完全图$G=(V,E)$，每条边都有对应一个权值。试寻找一个简单的环路（不闭合），这个环路经过每个顶点恰好一次，并且总权值最小。
如下所示的图，图中有$n=5$个顶点，假设起点是A点，则从起点开始逐一访问其余顶点形成的所有可能路径是其余4个点的排列$P{(}_{n-1}^{n-1})$，使用动态规划的话，能

动态规划的解法思路是：
对于一个子集$S\subseteq \{1,2,...,n\}$且$1\in S,j\in S.$
让$C(S,j)$表示从起点$1$开始经过了集合$S$中所有顶点一次且终止于$j$的路径的最短长度。将$C(S,j)$表示为更小的子问题：
$$\begin{gathered} C(S,j)=minC(S-\{j\},i)+d_{ij} \\ C(\{1\},1)=0 \end{gathered}$$

有了以上的递推公式，便能进行相应的动态规划算法设计了，先从大小为2的集合$S(|S|=2,且起点1\in S)$开始，赋值$C(S,1)=\infty$，找出$S$中的元素$j(j̸=1，j非起点)$，对$C(S,j)$执行上述递推公式。之后逐渐扩大集合S的大小直至$n$，并重复上述步骤。

伪代码：
$C(\{1\},1)=0$
for h=2 to n do
  for all subsets $S\subseteq \{1,2,...,n\}$ of size h and containing 1 do
   $C(S,1)=\infty$
   for all $j\in S,j̸=1$ do
    $C(S,j)=minC(S-\{j\},i)+d_{ij}$
return $mi{n}_{j}C(\{1,2,...,n\},j)+d_{j1}$

这种算法思路清晰，但是在实现算法的时候，需要设计合适ADT来表示图及顶点集合，我尝试过编写代码，但限于没有较好的ADT实现思路，我便放弃了 。