《机器学习实战》第五章:Logistic回归(2)随机梯度上升和一个实例
1. CH2-kNN(1)
2. CH2-kNN(2)
3. CH2-kNN(3)
4. CH3-决策树(1)
5. CH3-决策树(2)
6. CH3-决策树(3)
7. CH4-朴素贝叶斯(1)
8. CH4-朴素贝叶斯(2)
9. CH5-Logistic回归(1)
10. CH5-Logistic回归(2)
======== No More ========
这篇博客:
(1)接着上篇博客的那个简单实例,改进一下算法
(2)来一个大一点的实例:从疝气病症预测病马的死亡率
-------------------------------------------------------------------------------------
随机梯度上升
上篇博客里介绍的梯度上升算法,在每次更新回归系数的时候都要遍历整个数据集。如果训练样本数量有数十亿,每个样本的特征又有上千万个,那计算复杂度就太高了。
一种改进方法是:每次仅用一个样本点来更新回归系数。该方法称为随机梯度上升算法。
先来看个原型。只是原型。
def stocGradAscent0(dataMatIn, classLabels):
dataMatrix = array(dataMatIn)
m, n = shape(dataMatIn)
alpha = 0.01
weights = ones(n) #weights为numpy.ndarray类型
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights传进来的参数dataMatIn和classLabels都是List类型。首先把dataMatIn转成array类型(即numpy.ndarray类型)。这里和上篇博客gradAscent函数的处理方式不同,gradAscent是把dataMatIn转成Matrix类型。原因是之前我们做的事矩阵间的乘法,而这里我们做的是行向量间的乘法,用array型即可。
从第6行开始的循环:
对每个数据点,计算它对应的向量和weights向量的外积,作为sigmoid函数的输入得到输出(是一个数值),计算这个数值和该数据点的标签的差值,然后按照老方法更新weights向量。
看下效果。
dataMat, labelMat = loadDataSet()
weights=stocGradAscent0(dataMat, labelMat)
plotBestFit(dataMat, labelMat, weights)
我们先在外层加它个200次迭代。
def stocGradAscent0(dataMatIn, classLabels):
dataMatrix = array(dataMatIn)
m, n = shape(dataMatIn)
alpha = 0.01
weights = ones(n) #weights为numpy.ndarray类型
for j in range(200):
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights
然而,作者又说了,一个判断优化算法优劣的可靠方法是看它是否收敛。也就是说参数是否达到了稳定值,是否还会不断地波动?
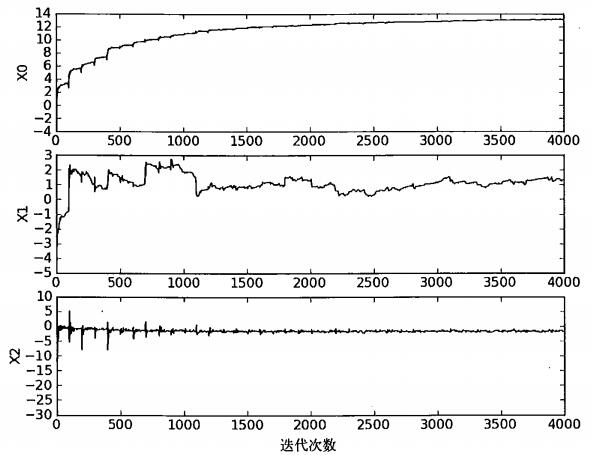
我们来看下三个回归系数随着迭代次数上升的变化情况。
首先,为什么迭代200次,而横坐标达到了20000?因为内层还有100个循环啊...
好,可以看出,X2这个系数,迭代了50次左右就达到了稳定值,而X0和X1需要更多次迭代。
然后,可以看到,在大的波动停止后,还有一些小的周期性波动。
原因是训练集中存在一些不能正确分类的样本点(数据集并非线性可分)。
我们还需改进算法,来避免波动,从而收敛到某个值。而且收敛速度要加快。
以下是作者写的“改进的随机梯度上升算法”。作者本人的源代码。我没动过。
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = shape(dataMatrix)
weights = ones(n) #initialize to all ones
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
return weights很好。接下来我又要吐槽一番了。
代码里有明显的纰漏!明显的纰漏!明显的纰漏!
首先,这个dataMatrix必须是array型。这个调用的时候必须注意,因为loadDataSet()函数返回的都是List型。
然而这不是重点。
来,注意代码的第8行和倒数第2行,作者原话:“每次从列表中选出一个值,然后从列表中删掉该值”。也就是说,每次从100个样本里随机选取一个,而且不能重复。
我们看看他到底做了些啥。举个例子吧。
假设m=5。每轮循环,一开始dataIndex是[0,1,2,3,4],len(dataIndex) = 5
假设第一次 randIndex 选了[0,1,2,3,4]中的2。没问题,我们于是使用dataMatrix[2]这个样本,然后从dataIndex里删掉了[2]这个元素,即2。现在dataIndex变成了[0,1,3,4],len(dataIndex) = 4
第二次 randIndex 要在[0,1,2,3]中选一项。不小心又选到了2,于是又使用了一遍dataMatrix[2]这个样本,然后从dataIndex里删掉了[2]这个元素,即3。现在dataIndex变成了[0,1,4],len(dataIndex) = 3
显然有毛病啊!这样的话,删除dataIndex里元素的作用就只是减小它的size,而没起到去重的作用...而且,每次随机选取的范围里面都有0,那岂不是每次都有可能用到dataIndex[0]这个样本,而且dataIndex[0]被抽到的概率将越来越大?
按常理,应该是选到了2这个下标后,我们就应该取dataIndex里找[2]这个元素,然后使用dataMatrix[dataIndex[2]]这个样本,而不是dataMatrix[2]。所以我改了下代码:
def stocGradAscent1(dataMatIn, classLabels, numIter=150):
dataMatrix = array(dataMatIn)
m, n = shape(dataMatIn)
weights = ones(n) #weights为numpy.ndarray类型
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not go to 0 because of the constant
randIndex = int(random.uniform(0,len(dataIndex)))
theChosenOne = dataIndex[randIndex]
h = sigmoid(sum(dataMatrix[theChosenOne]*weights))
error = classLabels[theChosenOne] - h
weights = weights + alpha * error * dataMatrix[theChosenOne]
del(dataIndex[randIndex])
return weights这样应该符合作者的原意了。
但这样的话,问题又来了。我每次确实是随机选取了一个样本,而且每次都不一样。
但是!内层循环次数是100,也就是说归根结底还是把每个样本都遍历了一遍,只不过遍历的顺序打乱了而已。
这样一来,跟之前的代码有什么区别?有什么区别?有什么区别?
这是很让我费解的一个地方。
不管了,先看下其他变动的地方。
numIter是外层迭代次数,可以调整,默认150
步长alpha的值在遍历到每个样本的时候都会变调整。alpha会随着迭代次数不断减小,但永远不会减小到0,因为还有个常数项0.0001。这样做的原因是保证在迭代多次之后新数据仍然具有一定的影响。
另外,我们这个常数选的是0.0001,比上篇博客标准梯度上升法里的0.01小了很多。这样选择的原因,这位大神的说法很到位:因为标准梯度下降的是使用准确的梯度,理直气壮地走,随机梯度下降使用的是近似的梯度,就得小心翼翼地走,怕一不小心误入歧途南辕北辙了。
看下效果吧。
dataMat, labelMat = loadDataSet()
weights=stocGradAscent1(dataMat, labelMat)
plotBestFit(dataMat, labelMat, weights)外层循环150次,效果还不错。
作者还给了三个回归系数随着迭代次数上升的变化情况,当然,是按他自己写的代码来测试的。
作者说,这里的系数没有像之前那样出现周期性波动,这归功于样本随机选择机制。
其次,水平轴比之前的短了很多,说明收敛速度更快。
我不明白:随机选择机制为什么可以减小波动,加快收敛速度?
按我的理解,需要指出来的是,“随机梯度上升”中的“随机”,意思并不是指每次一定要随机选取一条样本来更新weights。它的实际意思是用近似方法来改善标准梯度下降的时间复杂度,具体的做法是每次选取一条样本(而非所有样本)来近似地计算梯度、更新weights。
-------------------------------------------------------------------------------------
实例:从疝气病症预测病马的死亡率
讲真,这一章看到这里,感觉很郁闷。先是上一篇博客里提到的,作者没讲清楚我们究竟要对哪个函数求梯度(还好我有精力找到答案)。然后又是这里,作者没讲为什么选单条样本的时候,随机选就可以加快收敛速度(我已经没精力去探个究竟了)。
然而最后还是硬着头皮看个实例吧。
每个数据21个特征,1个标签,二分类。
作者说,拿到数据的时候,还处理了数据中的缺失值:
(1)用0来代替缺失的特征值。好处在于如果某个训练样本,如果有个特征的值为0,那么根据系数更新公式,这个特征对应的那项系数将不会更新。所以没影响。
(2)标签确实的样本直接扔了。
把数据集分成了训练样本horseColicTraining.txt 和 测试样本horseColicTest..txt
看一眼数据集:
上代码。
def classifyVector(inX, weights):
prob = sigmoid(sum(inX*weights))
if prob > 0.5: return 1.0
else: return 0.0
def colicTest():
frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')
trainingSet = []; trainingLabels = []
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr =[]
for i in range(21):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[21]))
trainWeights = stocGradAscent1(trainingSet, trainingLabels, 1000)
errorCount = 0; numTestVec = 0.0
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr =[]
for i in range(21):
lineArr.append(float(currLine[i]))
if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]):
errorCount += 1
errorRate = (float(errorCount)/numTestVec)
print "the error rate of this test is: %f" % errorRate
return errorRate
def multiTest():
numTests = 10; errorSum=0.0
for k in range(numTests):
errorSum += colicTest()
print "after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests))代码一目了然。
classifyVector 用来给测试数据进行分类。
multiTest 是多次统计colicTest的错误率。
看下效果。
multiTest()调整迭代次数和步长,会进一步降低平均错误率。