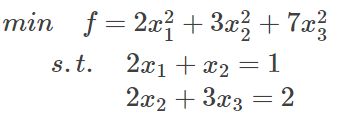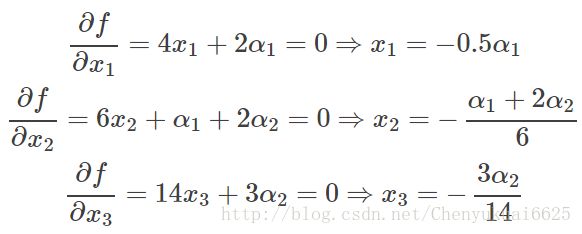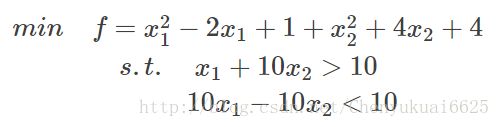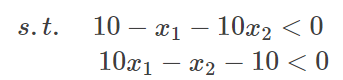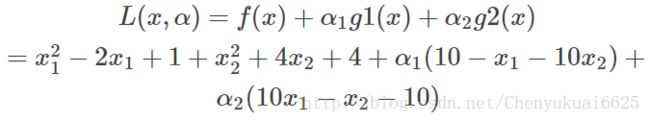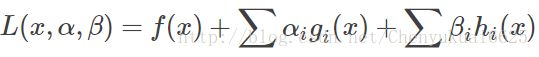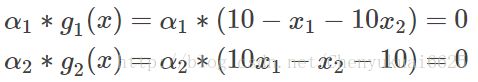SVM算法（一）（有监督学习）

一、SVM算法简介
1.1、什么是SVM算法？
  SVM(Support Vector Machine)算法，即支持向量机算法，它是最优秀的分类算法之一，也是数据挖掘十大算法之一，它以其简单的理论构造了复杂的算法，又以其简单的用法实现了复杂的问题而受到业界的青睐。SVM算法属于有监督学习算法。它是在1995年由Corinna Cortes和Vapnik首先提出的。
  SVM算法是基于统计学习理论的一种机器学习方法，它通过寻求结构化风险最小来提高学习机泛化能力，实现经验风险和置信范围的最小化，从而达到在统计样本量较少的情况下，亦能获得良好统计规律的目的。如今它常用来对小样本、非线性及高维数据进行模式识别、分类以及回归分析，并可以取得很好的效果。
1.2、SVM算法的核心思想
  SVM的核心思想可以归纳为以下两点：
  （1）它是针对线性可分情况进行分析，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分，从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能。
  （2）它以结构风险最小化理论为基于在特征空间中构建最优分割超平面，使得学习器得到全局最优化，并且在整个样本空间的期望风险以某个概率满足一定上界。
  最后，简单解释一下支持向量机的含义，支持向量的含义是指支持 or 支撑平面上把两类类别划分开来的超平面的向量点，“机”的意思就是算法。在深入讲解SVM实现过程之前我们需先了解简单的线性分类器。

二、线性分类器
2.1、超平面的概念
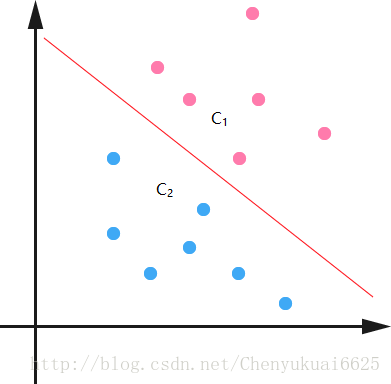
  以一个二维平面为例来说明分类方法，如下图所示，平面上有两种不同的点，分别用两种不同的颜色表示，一种为红颜色的点，另一种则为蓝颜色的点，我们希望找到一个决策面使得C₁和C₂两类数据分开。

  由上图可知红颜色的直线可以将数据很好的分成两类，它是一个分类函数，我们也把这条直线称之为超平面，在三维空间中超平面就是一个平面。一般的，如果一个线性函数能够将样本完全正确的分开，就称这些数据是线性可分的，否则称为非线性可分的。
2.2、找到最优超平面的目标函数和约束条件（第一步）
  上面我们知道超平面（红颜色的直线）可以将两类数据分开，这个超平面一般表示就是W^TX+b=0,现在的问题是找到对应的W和b使得分割最好。

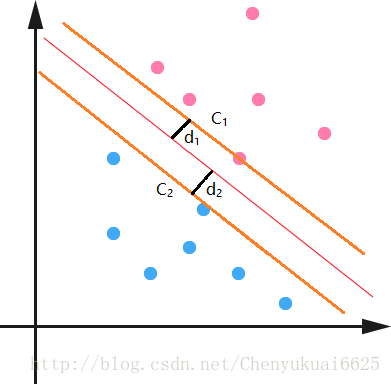
  先定义一下离这个线最近的点到这个分界面（线）的距离分别为d₁,d₂。那么SVM找最优权值的策略就是，先找到最边上的点，再找到这两个距离之和D，然后求解D的最大值。假设找到了这样一个分界面W^TX+b=0，那么做离它最近的两类点且平行于分类面，如上面的橙线所示。再假设我们有这两个虚线，那么真实的分界面我们认为正好是这两个分界面的中间线，这样d₁就等于d₂了。因为真实的分界面为W^TX+b=0，那么就把两个橙线分别设置为W^TX+b=1和W^TX+b=-1。可以看到橙线相对于真实面只是上下移动了1个单位距离，可能会说你怎么知道正好是一个距离？确实不知道，就假设上下是k个距离吧，那么假设上橙线现在为W^TX+b=k。两边同时除k可以吧，这样上虚线还是可以变成W^T₁X+b₁=1。同理下虚线也可以这样，然后他们的中线就是W₁^TX+b₁=0。可以看到从k到1，权值无非从w变化到w₁,b变到b₁,我在让w=w₁,b=b₁，不是又回到了起点吗，也就是说，这个中间无非是一个倍数关系。所以我们只需要先确定使得上下等于1的距离，再去找这一组权值，这一组权值会自动变化到一定倍数使得距离为1的。
  再看看D=d₁+d₂怎么求吧，假设分界面为W^TX+b=0，再假设X是两维的，那么分界面再细写出来就是：w₁x₁+w₂x₂+b=0。上分界线：w₁x₁+w₂x₂+b=1，下分界线：w₁x₁+w₂x₂+b=-1。所以由距离公式计算得到两条直线之间的距离为：D=d₁+d₂=2/||W||。
  W=(w₁,w₂)，W是个向量，||W||为向量的距离，||W||²=W^TW。所以要求D的最大值等效为求W^TW的最小值。因此优化问题就变为min(0.5*W^TW),乘一个系数0.5没影响，但是在后面却有用。
  如果一个一次函数分界面为W^TX+b=0，那么线上方的x可以使得W^TX+b>0，下方的x可以使得W^TX+b<0,那么对于上界面以上的点就有W^TX+b>1，对于下界面以下的点就有W^TX+b<-1。因为上界面以上的点的分类标签为1，下界面以下的点的分类标签为-1，所以可以将数据和标签归纳为一个式子：y_i(W^Tx_i+b)≥1。最终的带约束的优化问题转化为：
            min   0.5*W^TW
            s.t.   y_i(W^Tx_i+b)≥1  同等于 1-y_i(W^Tx_i+b)≤0
  注意的是这可不是一个约束条件，而是对所有的每个样本xi都有一个这样的约束条件。 目标函数W^T∗W是凸函数，所以满足KKT条件，可以引入拉格朗日乘子法对目标函数进行优化。

三、拉格朗日乘子法和KKT条件
3.1、拉格朗日乘子法
  为什么需要拉格朗日乘子法？这是组合优化问题的需要，我需要利用拉格朗日乘子法来讲问题进行优化。以下面带约束的优化问题为例：

  这是一个带等式约束的优化问题，有目标值，有约束条件。如果没有约束条件，对f直接求导数为0的值，解得的x即为极小值，有可能有多个极小值，但是如果目标函数是凸函数，则只有一个极小值，该值即为最小值。而当有约束条件时，就不能通过对f直接求导解得最小值，此时就需要利用拉格朗日乘子法来对问题进行转化，因为是等式约束，所以可以把这个约束乘一个系数加到目标函数中去，这就相当于既考虑了原目标函数，也考虑了约束条件。比如上面的目标函数，将约束等式考虑进去就变为：

  因为与α₁,α₂相乘的部分都为0，所以α₁,α₂的取值为全体实数。现在这个优化目标函数中就没有约束条件了，分别对x求导等于0，结果如下：

  把上面三个式子带到约束条件中去，可以得到两个包含α₁和α₂的等式，从而求解得到α₁=−0.39,α₂=−1.63,这样再带回去求x就可以了。那么一个带等式约束的优化问题就通过拉格朗日乘子法完美的解决了。那么更高一层的，带有不等式的约束问题怎么办？那么就需要用更一般化的拉格朗日乘子法即KKT条件来解决这个问题。
3.2、KKT条件
   约束条件还有可能含有不等式的约束条件。这时需要强调一下KKT条件。以下面的方程为例：

  可将上面的不等式约束条件转化成下式：

  然后将不等式约束条件放到目标函数中去就变成：

  那么KKT条件的定理是什么呢？就是如果一个优化问题在转变完后变成：

  其中g是不等式约束，h是等式约束。此时KKT条件就是函数的最优值，同时必定满足下面条件：
  (1) L对各个x求导为零；
  (2) h(x)=0;
  (3) ∑α_ig_i(x)=0，α_i≥0
  前两个式子根据前面的讲解应该可以理解，重点是第三个式子不好理解，因为我们知道在约束条件变完后，所有的g(x)<=0，且α_i≥0，然后求和还要为0，所以要么某个不等式g_i(x)=0，要么其对应的α_i=0。
  通过上述分析后，分别对x₁、x₂求导数：

  此时根据KKT条件知α∗g(x)=0，从而得到：

  由KKT条件可知，要么g=0，要么α=0，上面式子有两个g和两个α，所以需要分四种情况讨论：讨论方法是两个一组进行讨论，比如现在就讨论α₁，α₂，让其他的α不变，为什么选或者至少选两个讨论呢，这是因为∑α_ig_i(x)=0，改变一个α肯定不行的。如果α比较多的话需要采用SMO算法来进行α的求解。
  这里有四种情况，正好两个α。分情况讨论：
  （1）α₁=α₂=0，那么看上面的关系可以得到x₁=1,x₂=−1,再把x的值带回到不等式约束中去，发现KKT第一个就无法满足（10-1+20=29<0)，29>0的。所以这种情况舍弃。
  （2）g₁(x)=g₂(x)=0，带进去解得，x₁=110/101;x₂=90/101,再带回去求解α₁，α₂，得到α₁=58/101，α₂=4/101，它们满足大于0的条件，这组解是成立的。
  （3）其他两种情况不满足条件，舍弃。
  所以可以看到通过讨论完以后就可以得到最优的解。 x₁=110/101=1.08;x₂=90/101=0.89。
接下来的问题就是求解最优超平面。请接着阅读SVM算法（二）。